KL散度
KL散度简介
KL散度的概念来源于概率论和信息论中。KL散度又被称为:相对熵、互熵、鉴别信息、Kullback熵、Kullback-Leible散度(即KL散度的简写)。在机器学习、深度学习领域中,KL散度被广泛运用于变分自编码器中(Variational AutoEncoder,简称VAE)、EM算法、GAN网络中。
KL散度是非对称的,这意味着 D(P||Q) ≠ D(Q||P)。
KL散度定义
KL散度的定义是建立在熵(Entropy)的基础上的。此处以离散随机变量为例,先给出熵的定义,再给定KL散度定义。
一个离散随机变量X的可能取值为X=x1,x2,…,xn,而对应的概率为pi=p(X=xi),则随机变量的熵定义为:
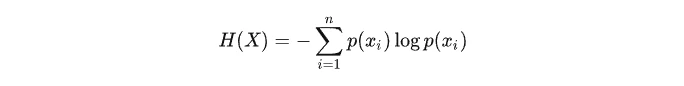
规定当p(xi)=0时,p(xi)log(p(xi))=0
如果是两个随机变量P,Q,且其概率分布分别为p(x),q(x),则p相对q的相对熵为:
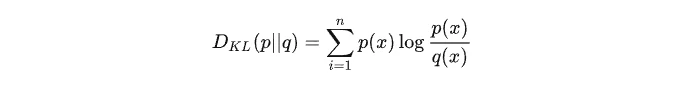
针对上述离散变量的概率分布p(x)、q(x)而言,其交叉熵定义为:
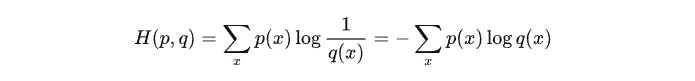
因此,KL散度或相对熵可通过下式得出:
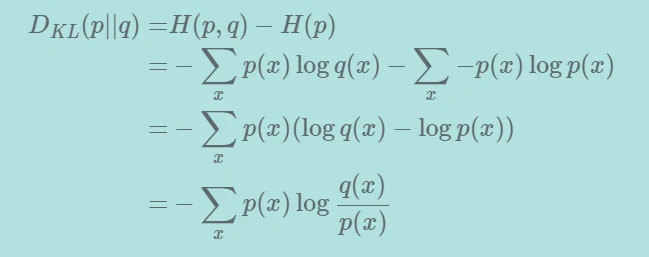
同样,当P,Q为连续变量的时候,KL散度的定义为:
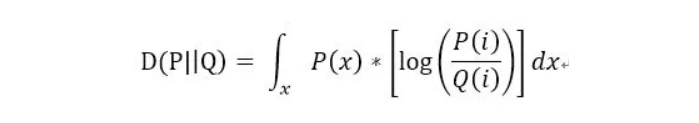
标准正态分布KL散度计算:N(μ, σ^2)与N(0, 1)
正态分布X~N(μ, σ^2)的概率密度函数为:
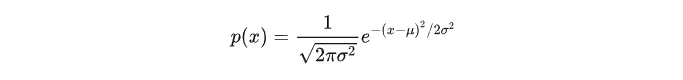
标准正态分布X~N(0, 1)的概率密度函数为:
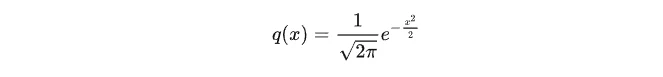
KL散度计算:
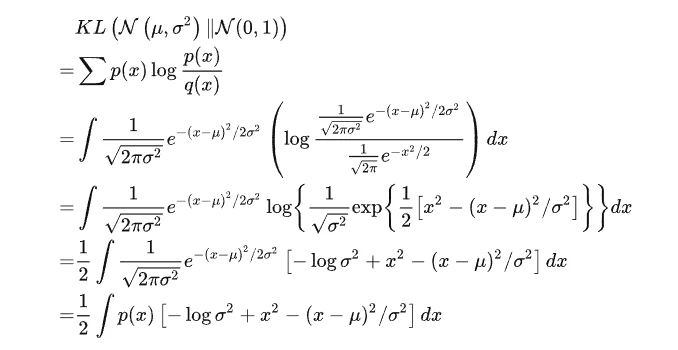
整个结果分为三项积分,第一项实际上就是 -log σ^2 乘以概率密度的积分(也就是 1),所以结果是 -log σ^2;第二项实际是正态分布的二阶矩,熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 μ^2 + σ^2 ;而根据定义,第三项实际上就是“-方差除以方差=-1”。所以总结果就:
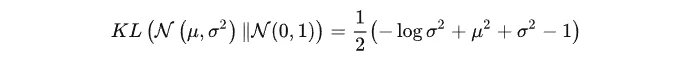
正态分布KL散度计算:N(μ_1, (σ_1)^2)与N(0, 1)
正态分布X~N(μ_1, (σ_1)^2)的概率密度函数为:
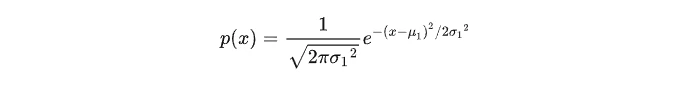
正态分布X~N(μ_2, (σ_2)^2)的概率密度函数为:
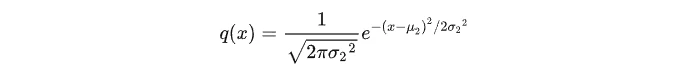
KL散度计算:
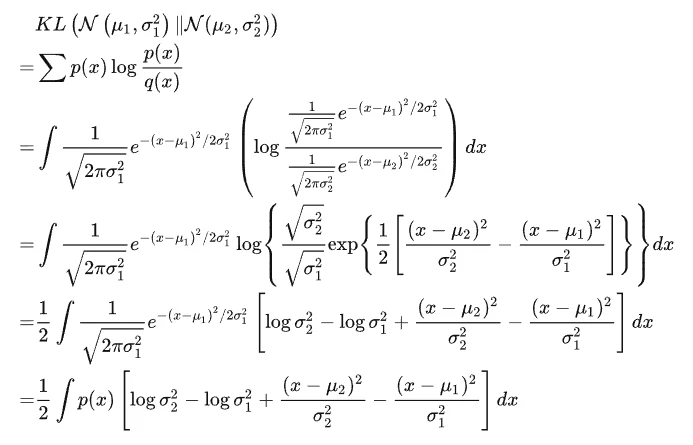
整个结果分为四项积分,第一项实际上就是 log (σ_2)^2 乘以概率密度的积分(也就是 1),所以结果是 log (σ_2)^2;第二项实际上就是 -log (σ_1)^2 乘以概率密度的积分(也就是 1),所以结果是 -log (σ_1)^2;第三项实际是异正态分布的二阶矩,熟悉正态分布的朋友应该都清楚异正态分布的二阶矩为 [(σ_1)^2+(μ_1-μ_2)^2]/[(σ_2)^2];而根据定义,第四项实际上就是“-方差除以方差=-1”。所以总结果就是:
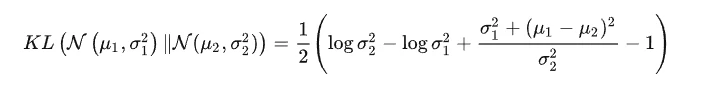
KL散度的意义
在统计学意义上来说,KL散度可以用来衡量两个分布之间的差异程度。若两者差异越小,KL散度越小,反之亦反。当两分布一致时,其KL散度为0。正是因为其可以衡量两个分布之间的差异,所以在VAE、EM、GAN中均有使用到KL散度。
参考资料
https://hsinjhao.github.io/2019/05/22/KL-DivergenceIntroduction/
https://zhuanlan.zhihu.com/p/365400000
https://zhuanlan.zhihu.com/p/521804938