aoi学院

Aisaka's Blog, School of Aoi, Aisaka University

论文阅读-图神经网络（GNN/GCN）论文精读

发表于 分类于 ， ， 阅读次数： Valine：
本文字数： 8.2k 阅读时长 ≈ 20 分钟

前言

原文地址：A Gentle Introduction to Graph Neural Networks

原文是一篇博客形式的文章，该文章最大的特点：全篇没有公式，完全用可交互的图来对GNN进行说明。因此，本文适合作为入门教学。

阅读本文前建议先读一读图神经网络（GNN）的基本原理

本文的内容：

  1. 什么样的数据最适合用图来表达？怎么将这种数据转为图数据？
  2. 是什么使图与其他类型的数据不同，以及我们在使用图时必须做出的一些特殊选择。
  3. 构建了一个GNN，并对其进行了详细地解释。
  4. 提供了一个GNN的playground，用户可以在其中选择参数在线训练GNN。

图是什么？

计算机专业的同学由于学过数据结构，对图肯定很熟悉了。本文给出得图的定义为：A graph represents the relations (edges) between a collection of entities (nodes).

即：图表示实体（节点）集合之间的关系（边）。

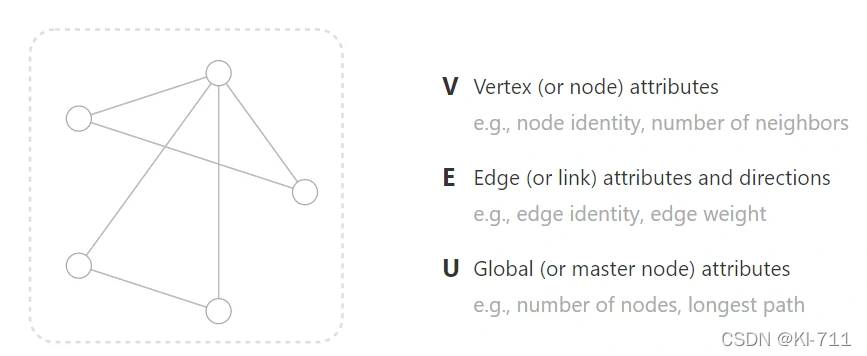
其中 V 表示顶点，E 表示边，U 表示全局（这个后面会有详细解释）。可以看到每一个定义后面都有一个attributes，这意味着我们不能只关注图的一个结构信息，还应该关注属性信息，比如节点的邻居数，边的权重，最长路径等等。

数据如何表示成图？

我们在现实生活中已经见过很多类型的图，比如社交网络：顶点为用户，边表示两个用户间存在某种联系，这很容易理解。

本节作者讲述了如何将两种（图像和文本）看似与graph不相关的数据表示成我们熟悉的graph数据。

图像

在CNN实战中，我们利用PIL包的Image来处理图像数据：

1
2
def Myloader(path):
    return Image.open(path).convert('RGB')

读入彩色图的时候，读出的是一个二维矩阵，矩阵中每个元素（像素）有RGB三个值。因此，我们通常将图像视为具有图像通道的矩形网格，每个像素代表一个节点，并与周围的像素点相连（8个）：

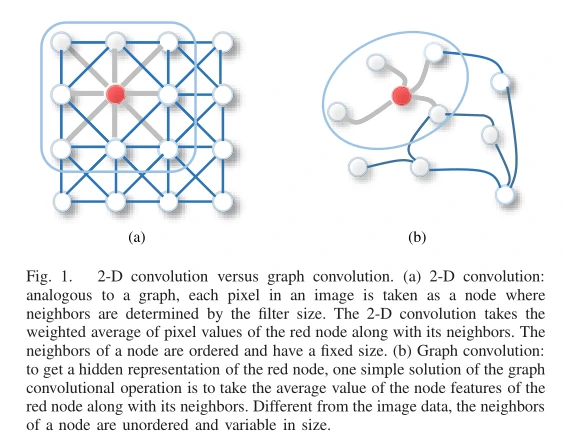
假设我们有一张图：244 × 244 × 3，高宽都是244，有RGB三个通道，那么我们该怎么把这个 244 × 244 × 3 的image表示为graph数据呢？

这里需要用到邻接矩阵A，假设我们以其中 25 × 25 个像素点为例：

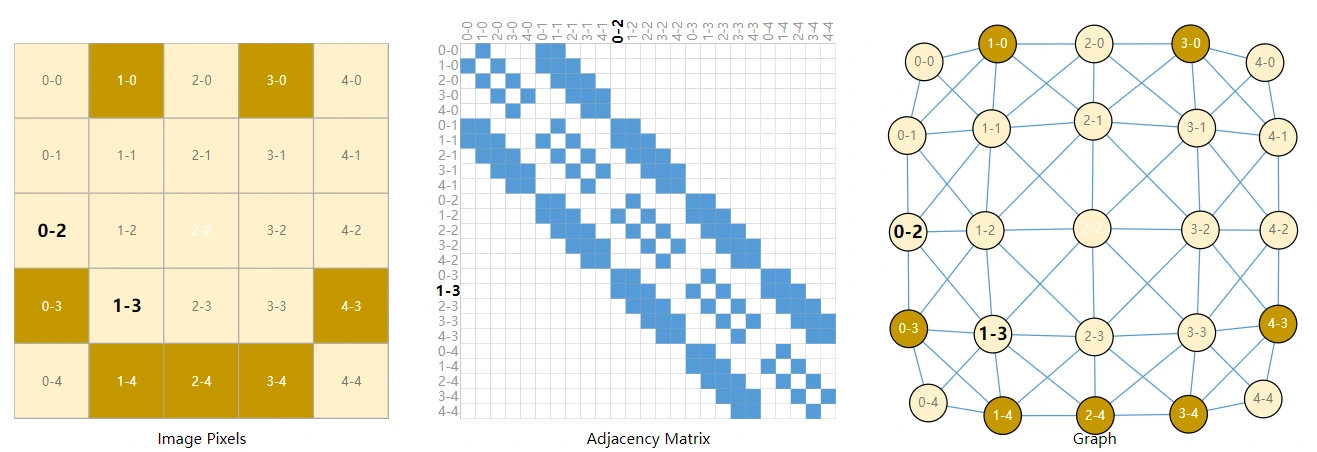
每一个像素点都和周围八个像素点相连，因此邻接矩阵中这八个位置都为1。

因此对于image数据，如果它有25 × 25 25 \times 2525×25个像素点，那么我们就能够建立一个拥有25个节点的图，每个节点可以跟其周围八个节点相连。

文本

文本可以被认为是一个序列，其中每一个词作为一个节点，每一个词和其下一个词之前有一条有向边：

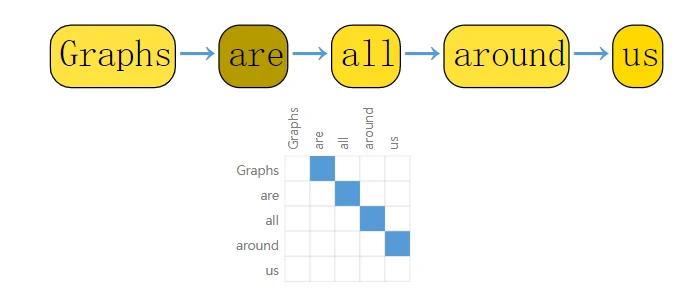
其他数据

除了上述图像和文本外，还有一些数据，除了图以外，我们很难用其他形式来表示他们！

分子

分子中原子通过作用力连在一起，因此每一个原子可以表示为一个点，原子间键表示为边。 如下图是一个香料分子：

以及咖啡因分子：

社交网络

社交网络除了graph外，我们很难再想出其他表示形式。在社交网络中，我们将个人表示为节点，将他们间的关系表示为边。

比如戏剧中人物关系图：

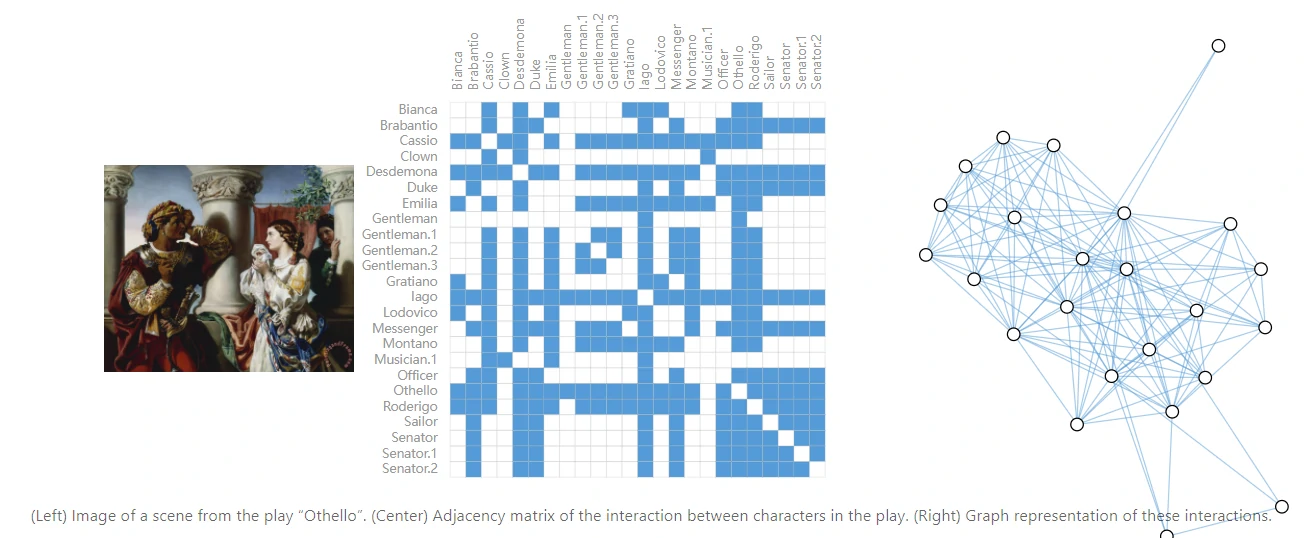
引文图

将论文抽象为节点，论文A引用了论文B，则有一条有向边A->B。

图中的任务

图里面的任务主要分为三大类：图级、节点级和边级。在图级任务中，我们预测整个图的属性。对于节点级任务，我们预测图中每个节点的一些属性。对于边级任务，我们希望预测图中边的属性或者是否存在这条边。

图级任务

在图级任务中，我们的目标是预测整个图的属性。 比如对于某一分子，我们可能想要预测该分子的气味，或者它是否会和与疾病有关的受体结合。

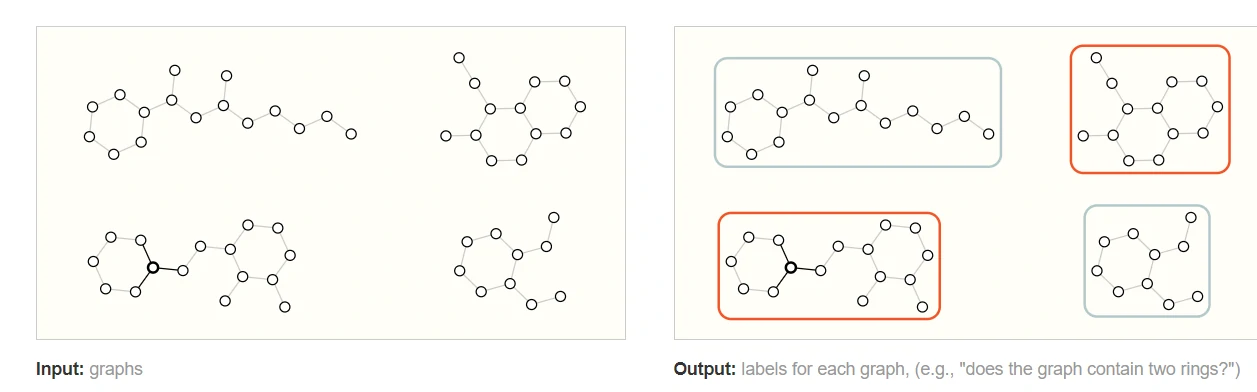
我们输入的是一张图，输出的是该图的label，比如该图是否有两个环？

节点级任务

节点级任务主要预测单个节点的属性。节点级预测问题的一个经典示例是空手道俱乐部数据集，该数据集是一个社交网络图，每个节点都具有一个唯一的label。

在network中：

1
2
3
G = nx.karate_club_graph()
nodes = list(G.nodes.data())
print(nodes)

输出为：

1
[(0, {'club': 'Mr. Hi'}), (1, {'club': 'Mr. Hi'}), (2, {'club': 'Mr. Hi'}), (3, {'club': 'Mr. Hi'}), (4, {'club': 'Mr. Hi'}), (5, {'club': 'Mr. Hi'}), (6, {'club': 'Mr. Hi'}), (7, {'club': 'Mr. Hi'}), (8, {'club': 'Mr. Hi'}), (9, {'club': 'Officer'}), (10, {'club': 'Mr. Hi'}), (11, {'club': 'Mr. Hi'}), (12, {'club': 'Mr. Hi'}), (13, {'club': 'Mr. Hi'}), (14, {'club': 'Officer'}), (15, {'club': 'Officer'}), (16, {'club': 'Mr. Hi'}), (17, {'club': 'Mr. Hi'}), (18, {'club': 'Officer'}), (19, {'club': 'Mr. Hi'}), (20, {'club': 'Officer'}), (21, {'club': 'Mr. Hi'}), (22, {'club': 'Officer'}), (23, {'club': 'Officer'}), (24, {'club': 'Officer'}), (25, {'club': 'Officer'}), (26, {'club': 'Officer'}), (27, {'club': 'Officer'}), (28, {'club': 'Officer'}), (29, {'club': 'Officer'}), (30, {'club': 'Officer'}), (31, {'club': 'Officer'}), (32, {'club': 'Officer'}), (33, {'club': 'Officer'})]

可以看到，每一个节点的标签要么为Mr. Hi，要么为Officer。在这种情况下，我们就可以建立一个模型对某一个节点的label进行预测。

因此，节点预测的输入是一个图，输出是节点的标签：

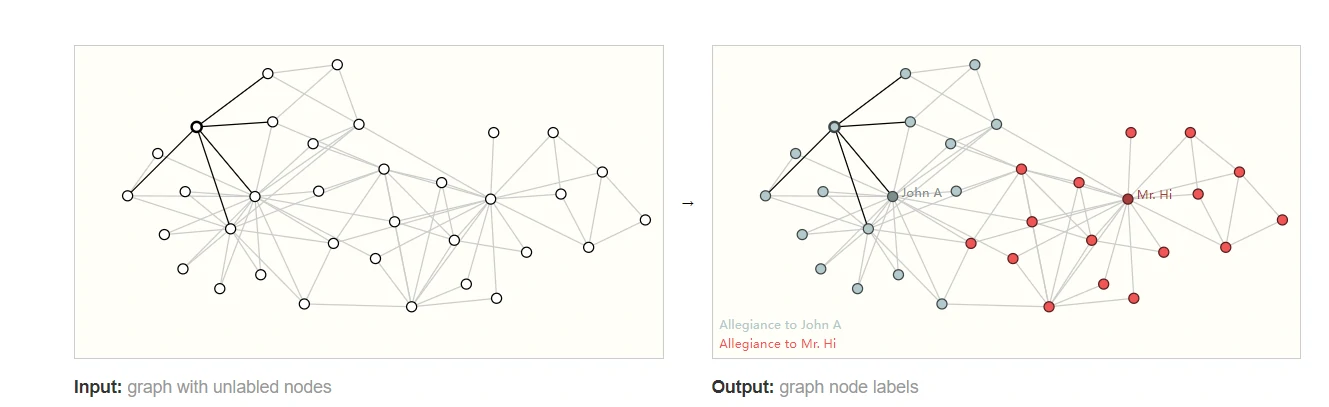
边级任务

对于边级任务：给定一些节点，我们希望预测这些节点中的哪些共享一条边或该边的权值是什么。

使用图数据的挑战

在使用神经网络对图进行处理前，我们得先将图表示成神经网络能够处理的数据类型。

图上的信息有四种：节点属性、边属性、全局属性以及连接性。

图表示的难点在于怎么来表示图的连接性。最容易想到的就是邻接矩阵：相连为1否则为0。

不过，使用邻接矩阵来表示连接性的缺点是显而易见的：对于一些大型网络，其节点数可能上百万，并且每个节点的边数变化可能会很大，比如某些节点连接了几万条边，有些节点只连接了一条边，这样邻接矩阵将会非常稀疏，虽然我们可以利用压缩的办法来对这些稀疏矩阵进行存储，但稀疏矩阵的计算一直都是一个难题。

此外，还有一个问题：对于同一个图，我们将矩阵中任何行或列之间进行交换：

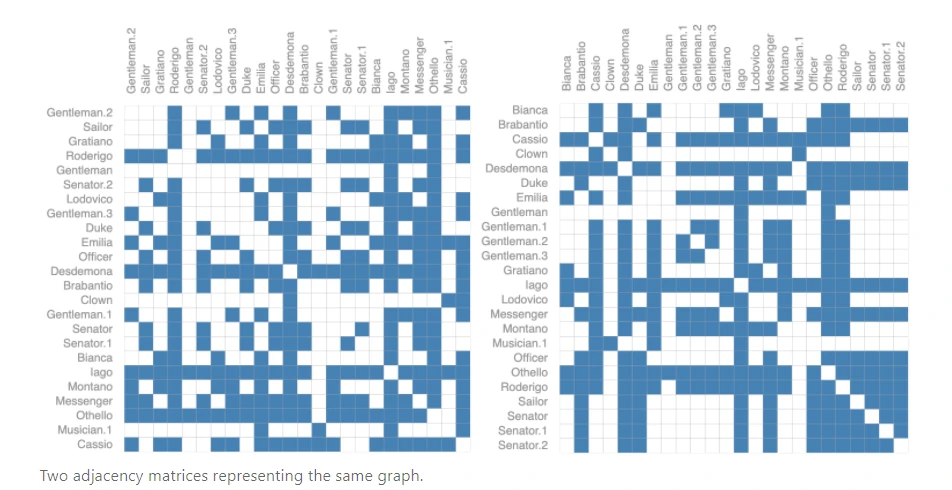
虽然两个邻接矩阵看起来不一样，但二者表示的却是同一个图。

也就是说，不同的邻接矩阵，可以表示相同的连接性！这意味着如果我设计了一个神经网络，在上述两个不同的矩阵输入后我得保证神经网络的输出是一样的。

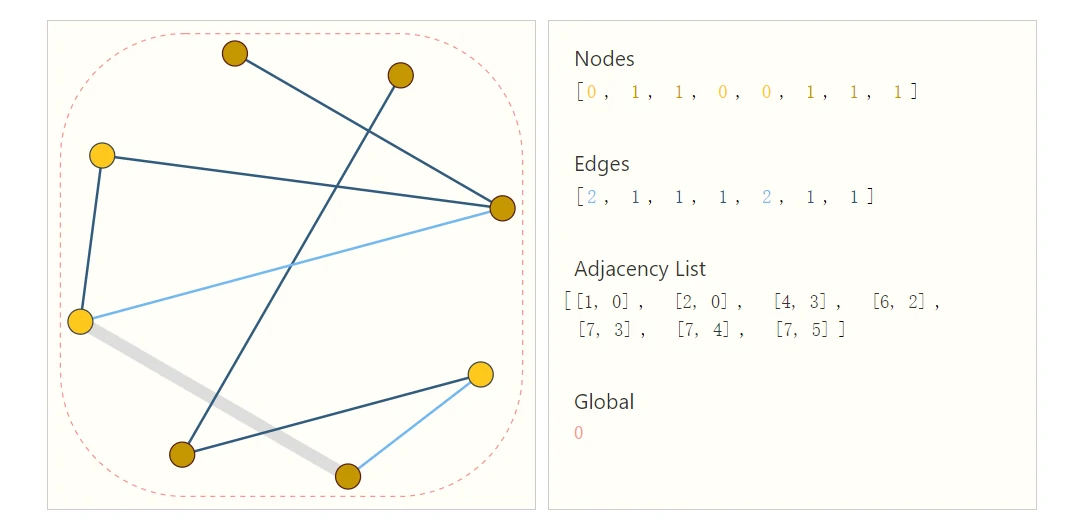
对于上面提到的两个问题，一个有效的解决方式是邻接表：

上图有8个顶点，7条边。对于每个顶点或者每条边的特征我们用一个标量（一般为向量）来表示，全局特征也用一个标量（一般为向量）来表示。对于连接性，不再用邻接矩阵来表示，而是用邻接列表来表示。

使用邻接列表来表示连接性的两个好处：

  1. 对于稀疏矩阵来说，使用邻接列表存储显然更加节省空间。
  2. 不存在两个不一样的邻接列表表示同一张图。

Graph Neural Networks

在经历了将数据转为graph以及将graph进行表示后，我们就能使用GNN来对图进行处理了。

一句话概括GNN：GNN是对图的所有属性（节点、边、全局上下文）进行的可优化的一种变换，它保留了图的对称性（置换不变性）。

简单来说就是，我们初始给定了节点或者边或者全局的属性，GNN将对这些属性进行变换，但是这种变换不会影响节点之间的连接性，变换优化后的图依旧保持着原图的连接结构。

当然，也只有在变换后依旧保持着原图的连接结构，我们才能使用这些变换后的属性对图进行预测。试想在一个社交网络中，原来有朋友关系的节点经过GNN的变换后不再具有朋友关系，此时再用这些变换后的属性对某一对节点进行预测，结果显而易见！

最简单的GNN

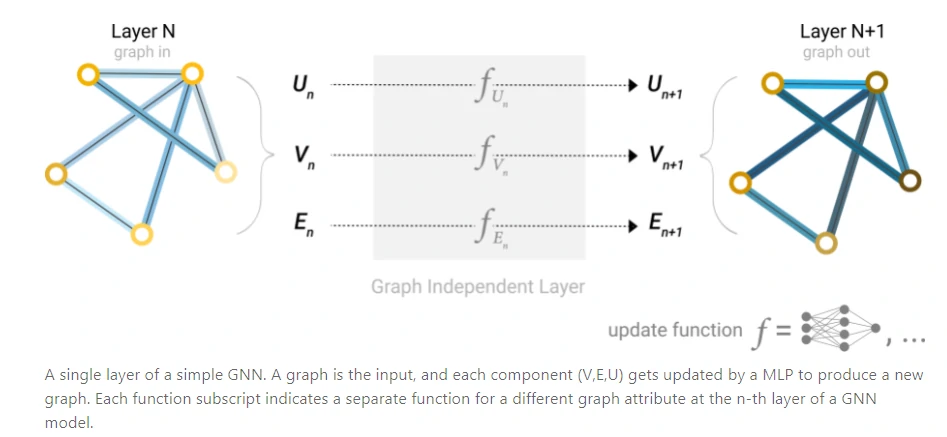
对于顶点状态向量、边状态向量还有全局的状态向量，我们分别构造一个输入大小等于输出大小的多层感知机，这里多层感知机其实就是我们在图神经网络（GNN）的基本原理中提到的状态转换函数fw。

经过MLP后，我们就得到了更新后的状态向量。

三个MLP组成了GNN的一层，经过GNN的一层后，原图的节点、边以及全局的状态向量都被更新过，但整个图的结构并没有发生变化。

GNN可以像一般的神经网络那样将多层进行叠加，以求来对图的状态向量进行多次更新。

Pooling

在图神经网络（GNN）的基本原理中我们需要一个gw函数来对状态向量进行转换输出，而gw可以是一个FNN。

对于一个简单的二分类问题，比如上面3.2节提到的空手道俱乐部网络图，我们需要对每个节点进行分类，在我们得到每个节点的状态向量后，我们可以搭建一个输出为2的全连接层，然后再经过一个Softmax，就能进行二分类了。多分类问题类似，只要将全连接层的输出改为n即可。

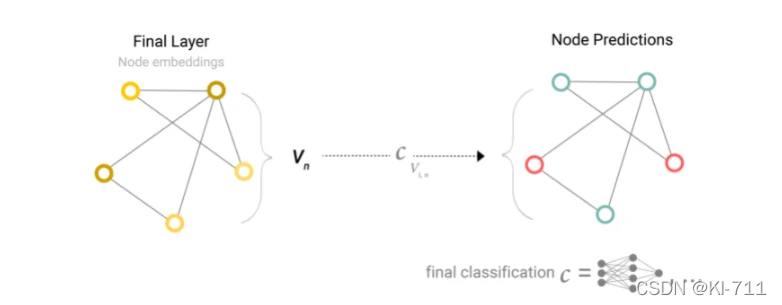
将经过最后一层后输出的节点状态向量Vn与一个全连接层相连，就能进行分类任务了。

值得一提的是，这里所有节点都是共用一个全连接层，也就是所有节点共享同一个全连接层的参数。

以上是最简单的一种情况，但我们不得不考虑另外一种情况：如果我们没有一个节点的向量表示，但我们仍想对该节点进行预测该怎么办？答案是Pooling，Pooling在CNN中已经有过接触。

具体如下所示：

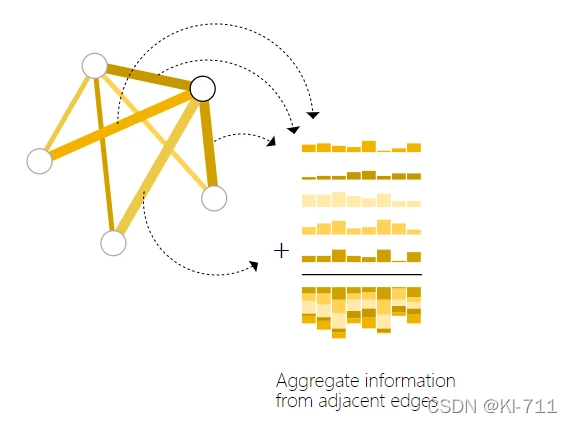
如果我们没有右上角那个节点的向量表示，此时我们就可以把与该节点相连的四条边的状态向量以及全局状态向量相加，得到这个节点的状态向量，然后再经过全连接层进行预测。

类似地，如果没有某条边的状态向量，只有节点的状态向量，如下所示：

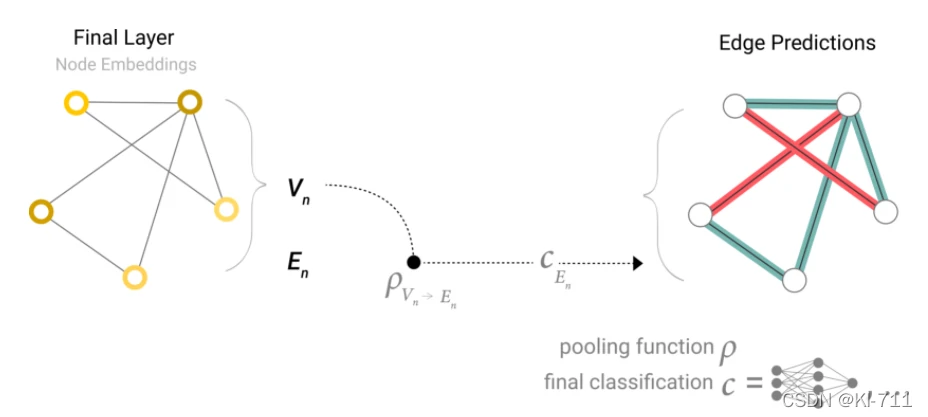
此时我们就可以把这条边上的两个节点的向量相加得到该边的向量，然后再进行预测。

又比如我们只有节点信息，没有全局信息，而我们想对图的全局标签进行预测：

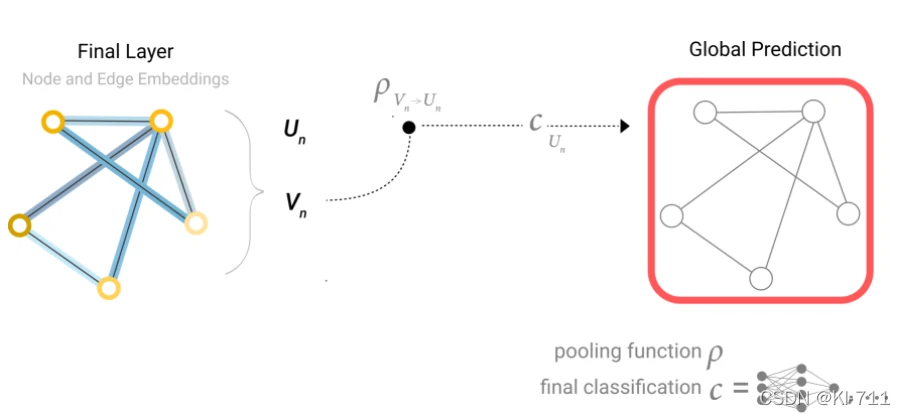
此时同样可以将图中所有顶点的向量加起来，得到一个全局表示，然后再进行预测。

因此，无论缺少哪一种信息，我们最终都能通过Pooling操作来汇聚已有的信息，进而得到我们想要的信息。

具体来讲，上面描述的GNN可以通过下图概括：

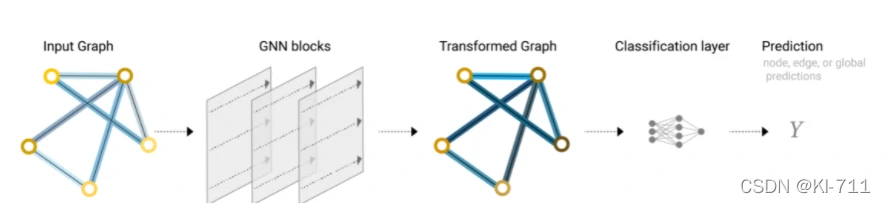
我们将原始graph通过一个个GNN层（每一层都有三个MLP，分别对三种状态进行转换），然后，无论是顶点、边还是全局，都通过同一个全连接层进行输出预测。

上述这种最简单的GNN存在着一个很明显的缺陷：我们在GNN层对节点或者边进行更新时，每层内所有节点共用一个MLP，所有边共用一个MLP，此时我们并没有考虑连接信息，也就是说我们在对节点更新时没有考虑与该节点相连的其余节点或者边，更新边时没有考虑与该边相连的节点。

简单来说，我们在更新时没有将图的结构信息考虑进去。

消息传递

那么我们怎么在更新时考虑结构信息呢？这点其实在图神经网络（GNN）的基本原理中已经详细叙述过了：

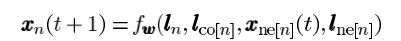
如下图所示：

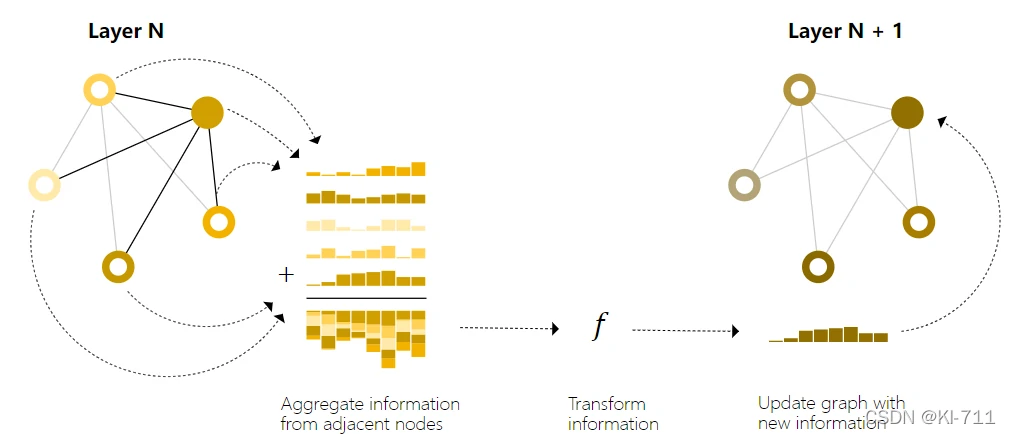
我们在更新每一个节点的向量时，并不只是简单地将该节点的向量通过一个MLP后得到更新后的向量，而是还要考虑与该节点相连节点的向量，也就是在下述更新公式中：

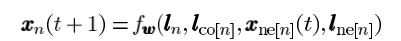
我们要考虑x_{ne[n]}这一项了。

当然上图这种更新方式并没有太复杂，只是将该节点的向量与其相连节点的向量相加。

考虑一种更为复杂的情况：

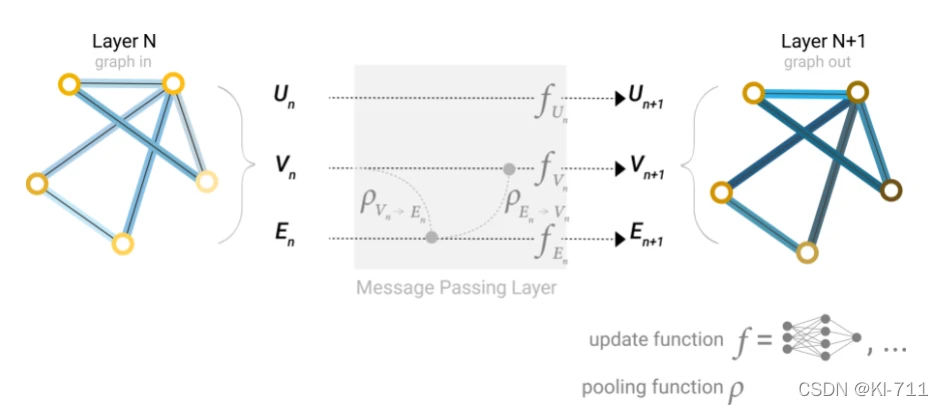
在进行边的更新时，我们可以将与该边相连的两个顶点的向量加入到该边的向量中（如果维度不同则需要变换），然后再对该边进行更新。同样，对于某一个节点的更新，我们也可以将与该节点相连的边的向量加入到该节点中，然后再对该节点进行更新。

节点和边之间的消息传递存在一个选择：

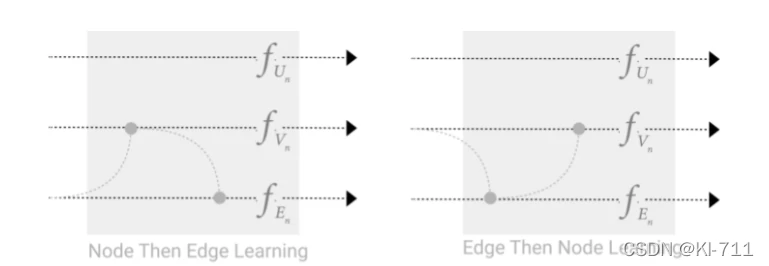
我们可以先把边的信息传递给顶点，顶点更新后，再将更新后的顶点信息传递给边，边再更新（上图左），或者相反（上图右）。

还有一种办法是交替传递：

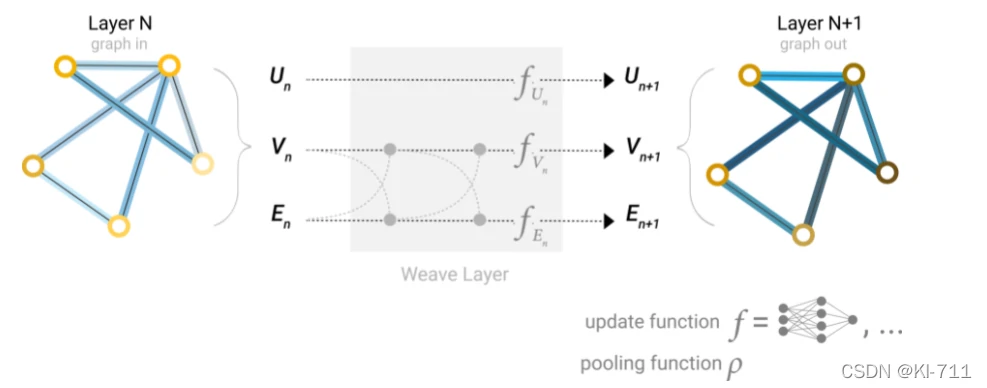
我们可以同时进行两种操作：将边的信息给节点，然后节点的信息也给边。此时的节点和边都包含了各自的信息，然后再进行一次传递，将二者的信息互相传递，随后再用两个MLP对节点和边进行更新。

全局表示

对一个large graph来讲，即使我们多次进行消息传递，图中相距较远的两个顶点间也可能无法有效地相互传输信息。

一种解决办法是加入master node（主节点）或者context vector（上下文向量）。主节点是一个虚拟的点，我们假设它与图中所有节点都相连，同时它也跟所有的边都相连。

因此在进行顶点或者边的更新时，如果我们加上全局表示U，就能保证所有顶点（边）间都能传递信息。

实验

原文作者做了一件很nb的事情：在网页中写了一个GNN的具体的演示程序：

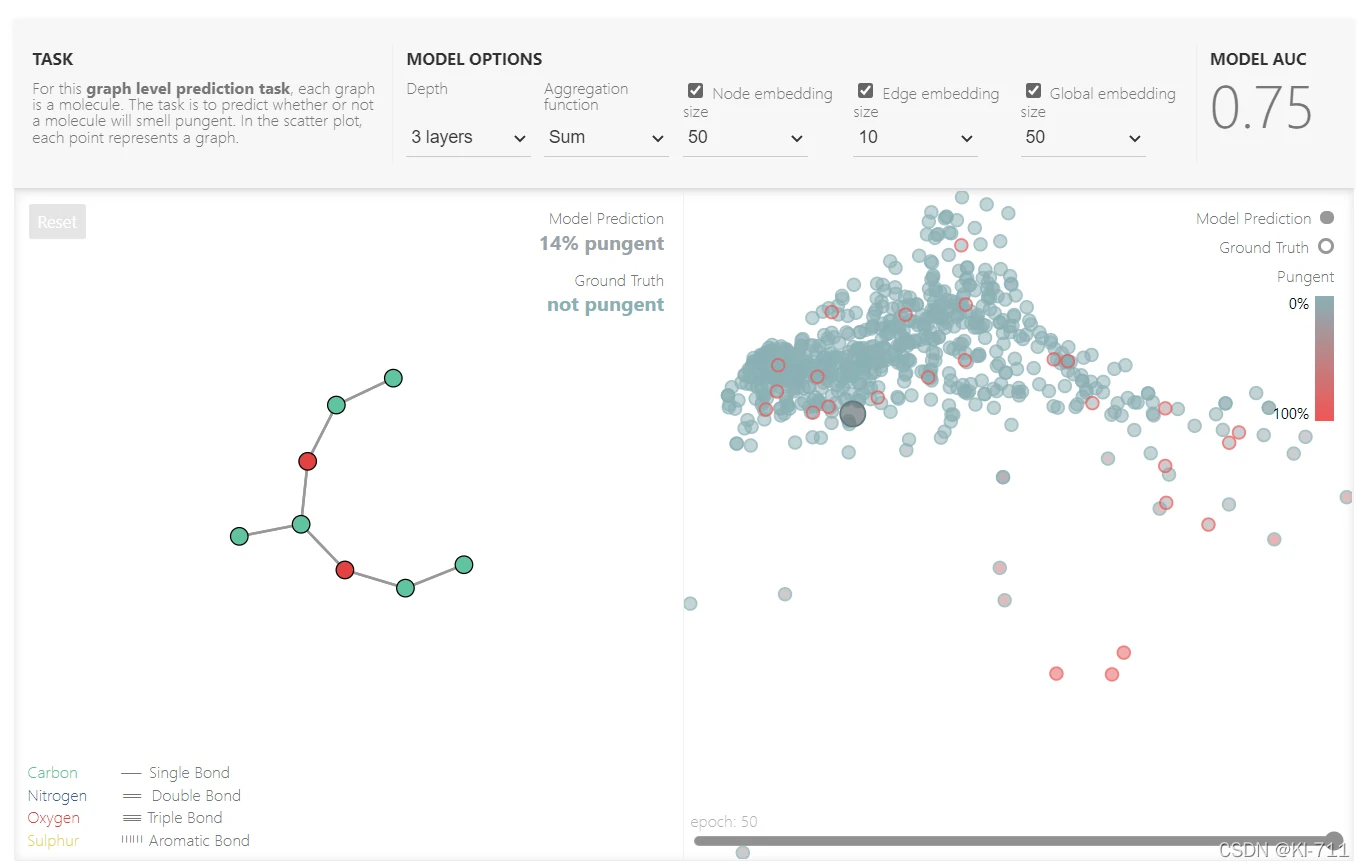
这个框架演示的是一个Graph Level的预测任务，每个图表示一个分子，我们的任务是预测该分子是否有刺鼻的气味。

在这个演示框架中，我们可以选择的参数有：GNN的层数、Pooling方式（Mean、Sum或者Max）、节点的嵌入维度、边的嵌入维度以及全局的嵌入维度。

每改变一次这些参数，该框架就会对数据重新训练一遍，然后再给出预测表现（AUC）。

作者通过多次试验，给出了不同的因素（如Pooling方式、嵌入维度大小等）对模型精度的影响，这里就不再细述了，有兴趣的可以自己去看一看原文。

相关知识

其他类型的图

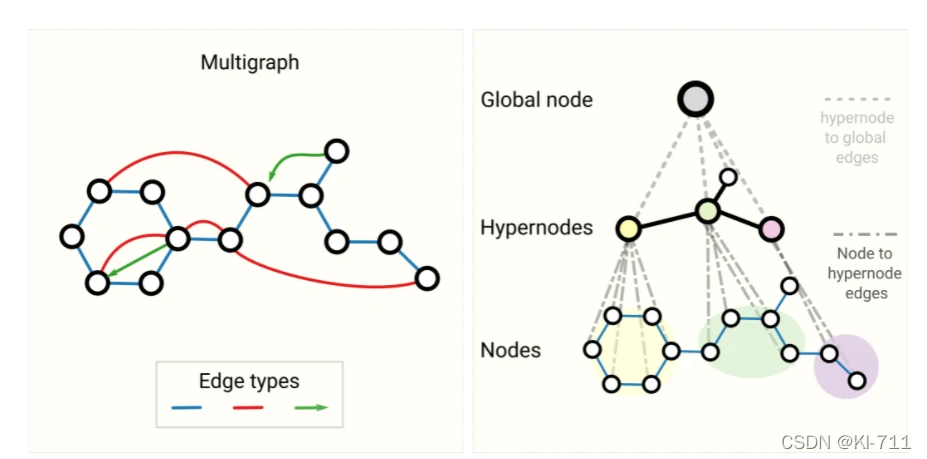
这里主要介绍了两种其他类型的图：多重图和嵌套图。

所谓多重图，就是指图中一对节点间可以有多种不同类型的边。比如在社交网络中，两个节点（用户）之间的边，可以表示这两人是熟人、家人或者情侣。这种情况下，GNN可以通过为不同类型的边设置不同类型的消息传递方式来进行调整。

所谓嵌套图，就是说图中的某一个节点可能就表示一个图。比如在一个分子网络中，一个节点代表一个分子，如果一个分子能通过某种反应转换为另一个分子，则两个分子之间有一条边。在这个网络中，节点（分子）本身也是一个图（原子-原子）。在这种情况下，可以让GNN学习分子级别的表示和另一个反应网络级别的表示，并于训练期间在它们之间进行交替。

此外，还有超图，超图的一条边可以连接到多个节点，而不仅仅是两个。对于这种情况，可以通过识别节点社区并分配连接到社区中所有节点的超边来构建超图。

采样和批处理

GNN存在邻居爆炸的问题，即：GNN会不断地聚合图中相邻节点的信息，第L层GNN中的每个目标节点都需要聚合原图中L层以前的所有节点信息。邻点爆炸式增长，使得GNN的minibatch训练极具挑战性。

此外，由于彼此相邻的节点和边的数目不同，我们也不能使用恒定的批量大小。

解决该问题的办法是从图中进行采样，得到一个子图，然后对子图进行处理。

对一张图进行采样的四种方式如下图所示：

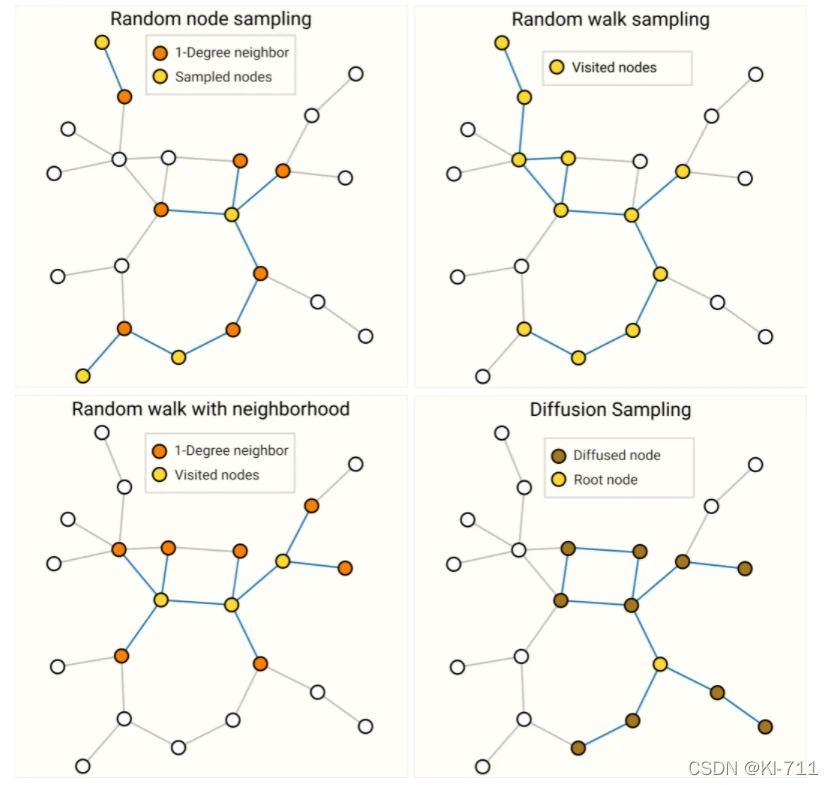
  • Random node sampling：先随机采样一些点（Sampled nodes），然后再采样它们的邻居。
  • Random walk sampling：做一些随机游走，从当前点的邻居节点中进行采样。
  • Random walk with neighborhood：结合前两种：先随机走一定长度，然后再采样它们的邻居。
  • Diffusion Sampling：取一个根节点，然后对它的一近邻、二近邻一直到K近邻进行采样，类似于一个BFS。

Inductive biases

先说一说CNN的平移不变性：即使目标的外观发生了某种变化，但是利用CNN依然可以把它识别出来。即图像中的目标无论是被平移，被旋转，还是被缩放，都可以被成功地识别出来。

而在GNN中，也具有图对称性：也就是排列无关性，即使交换了顶点的顺序，GNN对其的作用都保持不变。

不同的Pooling方式

在GNN中，对节点和边的信息进行Pooling是关键操作，选择一个最优的Pooling方式是一个比较好的研究方向。

常见的Pooling方式有max、mean和sum，作者对三者进行了比较：

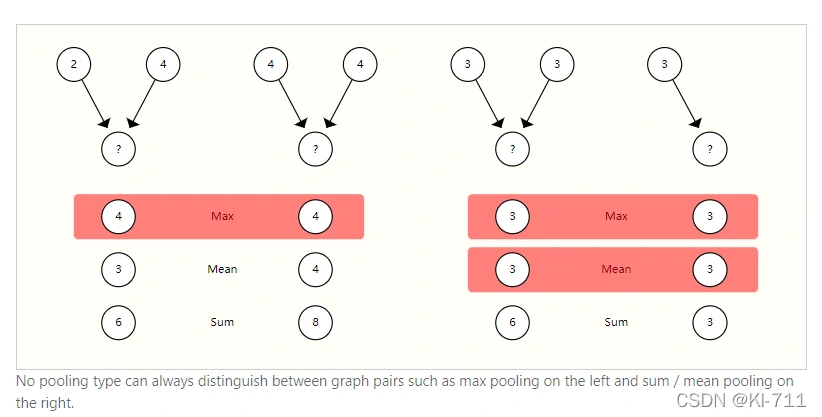
左边这幅图中，有2-4和4-4两个网络，如果我们采用max，二者结果都是4，没法进行区分，而mean和sum可以对二者进行区分；右边这幅图中，max和mean没法区分两种网络，而sum却可以。

因此，没有一个Pooling方式是明显优于其它Pooling方式的。

总结

在图神经网络（GNN）的基本原理中，我们给出了GNN的Forward过程：

原始论文中的Forward是通过一个repeat操作不断地对节点的状态进行更新。而状态转换函数fw实际上可以是一个神经网络，那么循环操作就可以用下图表示：

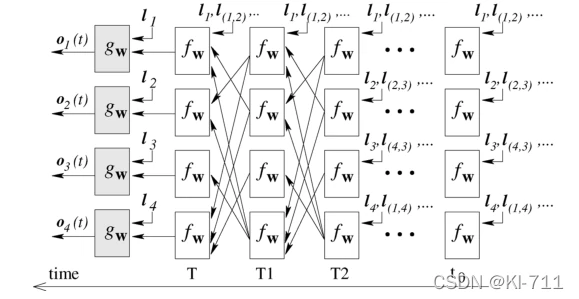
把上图中的fw理解为MLP（或者其他），就能与本文完整地对应起来了。

参考资料

https://www.bilibili.com/video/BV1iT4y1d7zP
https://staging.distill.pub/2021/gnn-intro/
https://blog.csdn.net/Cyril_KI/article/details/122050679