余弦距离

简单来说,余弦相似度,就是计算两个向量间的夹角的余弦值。
余弦距离就是用1减去这个获得的余弦相似度。
余弦距离取值范围
由上面的余弦距离可以知道,余弦距离的取值范围为[0, 2] ,这就满足了非负性的性质。
欧式距离
欧式距离之前提过了
就是常用的距离计算公式:
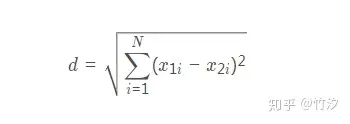
两者之间的关系
当向量的模长是经过归一化的,此时欧氏距离与余弦距离有着单调的关系:
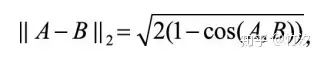
在此场景下,如果选择距离最小(相似度最大)的近邻,那么使用余弦相似度和欧氏距离的结果是相同的。
什么时候用余弦距离什么时候用欧式距离呢?
总体来说,欧氏距离体现数值上的绝对差异,而余弦距离体现方向上的相对差异。
例如,统计两部剧的用户观看行为,用户A的观看向量为(0,1),用户B为(1,0);此时二者的余弦距很大,而欧氏距离很小;我们分析两个用户对于不同视频的偏好,更关注相对差异,显然应当使用余弦距离。
而当我们分析用户活跃度,以登陆次数(单位:次)和平均观看时长(单:分钟)作为特征时,余弦距离会认为(1,10)、(10,100)两个用户距离很近;但显然这两个用户活跃度是有着极大差异的,此时我们更关注数值绝对差异,应当使用欧氏距离。
总结:在日常使用中需要注意区分,余弦距离虽然不是一个严格意义上的距离度量公式,但是形容两个特征向量之间的关系还是有很大用处的。比如人脸识别,推荐系统等。