摘要
情绪是人对外界事物产生的心理和生理反应。准确地识别情绪在人机交互研究中占据着重要位置，其成果可应用在医学、教育、心理、军事等方向。由于脑电信号具有客观, 不易伪装等特点, 其在情绪识别领域的应用广受关注。从脑电信号中提取与情绪关联大、区分能力强的特征, 有助于后续的分类器更有效地识别不同情绪状态。本文调研了目前常用于情绪识别研究领域的脑电信号特征, 从时域、频域、时频域和空间域 4 个方面介绍其定义、计算方法, 以及与情绪的联系。
引言
情绪是人对客观事物的态度体验及相应的行为反应 [1]，对于人类的行为和心理健康有着重要影响。如何准确识别情绪，在人机交互研究中占据重要位置，且有实际应用的意义：在医学方面，有助于对有心理疾病或表达障碍的患者进行疏导与诊断；在教育方面，根据听者的情绪施以不同的教学手段，可提高授课效率。在《国家中长期科学和技术发展规划纲要(2006∼2020)》中, 脑科学和人机交互均列为国家重大需求的关键技术, 而情绪识别技术将为其研究提供重要的理论依据。
为了识别情绪，研究人员需要对情绪状态进行量化和建模。目前广泛使用的情绪量化模型主要有离散模型和维度模型两种。在离散模型中，情绪空间由离散而有限的基本情绪构成，例如大多数心理学研究者公认的 6 种基本情绪 —— 高兴 (happiness)、悲伤 (sadness)、惊讶 (surprise)、恐惧 (fear)、愤怒 (anger) 和厌恶 (disgust)，其他情绪都可以由基本情绪组合而成 [2]。维度模型则是基于认知评价将情绪空间划分为效价 – 唤醒度 (valence-arousal, VA) 两个维度 [3]，或效价 – 唤醒度 – 优势度 (valence-arousal-dominance, VAD) 3 个维度 [4]，目前对于 VA 模型的研究比 VAD 模型更广泛。效价表示情绪是积极还是消极的；唤醒度反映情绪的强烈程度；优势度指人能否控制这种情绪。维度模型可将离散情绪映射至坐标空间，图 1 即为用 VA 模型表示高兴、恐惧和悲伤 3 种离散情绪。
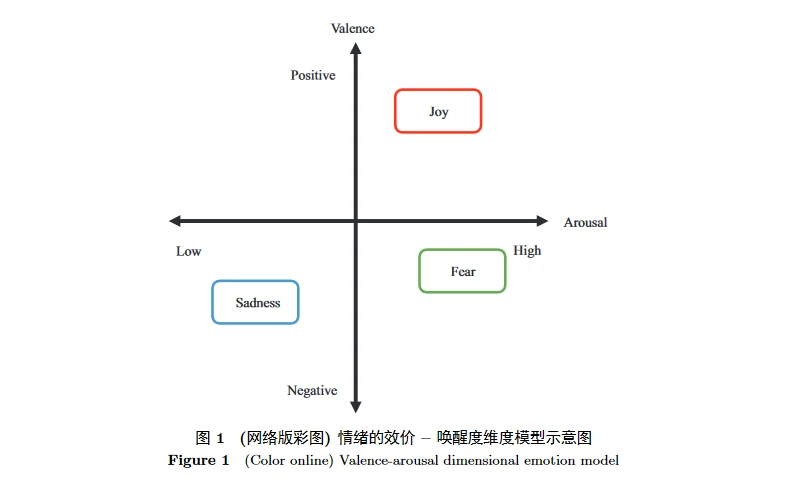
面部表情、语音语调、姿势动作和生理信号都可以作为情绪识别的数据来源，其中生理信号难以伪装，包含的信息也更丰富 [5]。使用生理信号识别情绪通常包括以下 6 步:
- 情绪诱发，使用图片、声音或视频等刺激材料诱发被试者产生特定类型的情绪
- 信号采集，通过设备采集被试产生情绪时的各种生理信号
- 信号预处理，通常使用滤波去除噪声和伪迹
- 特征提取，对信号进行变换。从中计算与目标任务相关的特征
- 用机器学习领域的分类算法进行情绪分类
- 以图表等形式反馈识别结果。
其中，特征提取是至关重要的一步，若能找出与情绪最相关的特征集合，有利于提高后续分类器的识别准确率。
在脑电 (electroencephalogram, EEG)、心电 (electrocardiogram, ECG)、肌电 (electromyography, EMG) 和皮肤温度 (skin temperature, SKT) 等生理信号中，使用脑电识别情绪具有操作简单、成本低、效果好的优势，近年来得到了广泛关注 [6]。脑电是记录头皮电位变化的信号，在一定程度上反映大脑皮层的活动。研究表明不同脑区参与不同的感知和认知活动，例如额叶 (frontal lobe) 与思维、意识有关，颞叶 (temporal lobe) 与人脸和场景等复杂刺激信息的处理、嗅觉和听觉有关，顶叶 (parietal lobe) 与多种感官信息的整合和对物体的操作控制有关，枕叶 (occipital lobe) 则与视觉有关 [7].
现有脑电特征的定义与计算方法
在情绪识别领域，EEG传统特征主要分为时域(time domain)特征、频域(frequency domain)特征、时频域(time-frequency domain)特征3类。考虑到脑区的不对称性也可以反映情绪信息, 空间域(space domain)特征也因此逐渐用于识别情绪。本节将从时域、频域、时频域、空间域4个角度介绍常用于情绪识别的脑电特征。
时域特征
大多数脑电设备以时域形式采集 EEG 信号，故时域特征最直观易得，其主要包括：事件相关电位、信号统计量、能量、功率、高阶过零分析、Hjorth参数特征、不稳定指数和分形维数。
脑电设备根据一定的采样频率对原连续信号进行采样, 得到离散序。 我们约定，用 s(n) 表示某个电极上第 n 次采样得到的 EEG 信号值, n = 1, 2, . . . , N , N 表示总采样数。
事件相关电位
事件相关电位 (event related potential, ERP) 是指由离散刺激事件引发的脑电电压波动，可反映认知加工的过程[8]。与不间断的脑电电压波动幅度相比，大多数 ERP 幅度小，因此通常取多段由相同刺激引发的 EEG 的平均值分析 ERP [9]。
ERP 的波形随时间变化呈现具有不同持续时间、振幅和极性的波峰，因而通常从 3 个方面来衡量：潜伏期 (latency)、振幅 (amplitude)、正负极性 (polarity)。图 2 是在 0 ms 时发生的刺激事件引发的 ERP 波形示意图。
- 潜伏期指大脑皮层从接受刺激到发生反应的延迟时间，通常计算刺激起始到波峰顶点间的时长。潜伏期与神经活动的加工时间有关，加工越久潜伏期越长。
- 振幅有基线 – 波峰和波峰 – 波峰两种测量方式，反映大脑的兴奋性高低，例如给被试呈现负性刺激材料时，ERP 的振幅会增加 [10]。
- 极性中的正性电压波动 (positive) 用 P 表示，负性 (negative) 用 N 表示 [11]。
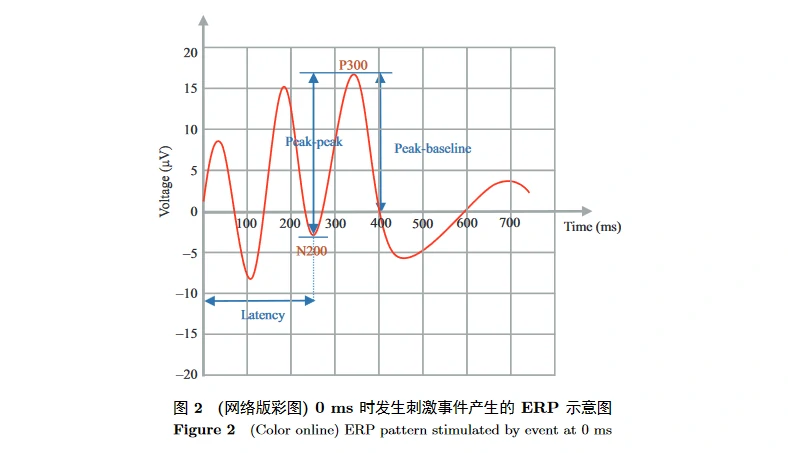
ERP 的成分一般遵循两种命名体系, 一种依据潜伏期, 例如 P300 表示电压向正性波动, 且潜伏期为 300 ms 左右; 另一种则依据成分的序列性, 例如刺激诱发的第 1 个显著的负成分为 N1, 第 3 个显著的正成分为 P3。ERP 成分的潜伏期数值往往约为序列位置的 100 倍, 所以第 1 种命名方式中的 P300 等价于第 2 种方式的 P3。
在情绪方面, 潜伏期较短的 ERP 成分与效价有关 [12∼15], 如枕叶的 P100 在产生消极情绪时的振幅大于积极情绪时的振幅 [16, 17]。P300 和潜伏期在 500 ms 以上的皮层慢电位 (slow cortical potential, SCP) 等潜伏期较长的 ERP 成分与唤醒度有关 [6, 18∼20]。由于 P300 的测量更可靠, 且其振幅和潜伏期特征包含的信息更丰富, 故 P300 为神经科学领域研究最多的 ERP 成分 [11]。Nieuwenhuis 等 [21] 的研究表明, P300 在正性或负性情绪下都比中性状态时更显著。
ERP 的瞬时分辨率强, 常用于由离散的视、听和触觉刺激诱发情绪的情况, 例如图片、短音频和振动等, 而不常用于连续的情绪诱发。在实时系统中, 情绪的触发点很难确定和控制, 所以 ERP 难以应用在情绪的实时诱发和检测中 [22]。
信号统计量
电信号通用的时域统计特征也可应用于 EEG 信号, 它们简单易计算, 且可以得到较好的识别效果 [23∼25]。 例如, 平均值 μ_s, 标准差 σ_s, 一阶差分绝对值的平均值:
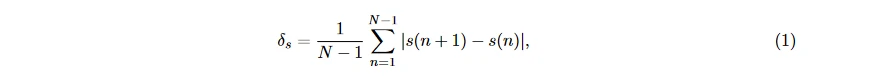
二阶差分绝对值的平均值:
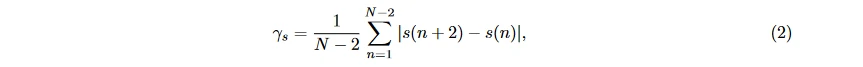
归一化的一阶差分 (也称为归一化长度密度, 可衡量脑电信号的自相似性 [26]):
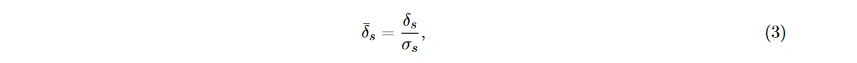
和归一化的二阶差分:
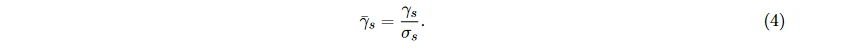
能量
大脑皮层的活跃程度影响 EEG 的振幅, 进而反映为能量的波动。信号的能量在时域上表示为幅度的平方, 即
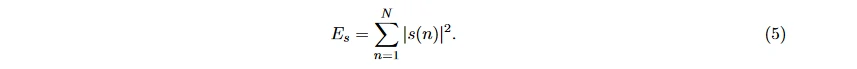
功率
平均功率可用能量除以采样数得到 [27], 在频域上也有能量和功率的计算方法, 将在 2.2 小节进行说明。
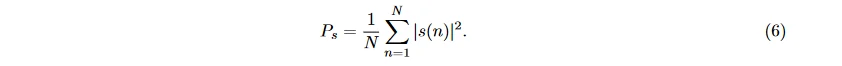
Hjorth 参数特征
Hjorth 定义了信号在时域上的 Hjorth 参数特征 [28], Activity 衡量信号波幅的偏离程度:
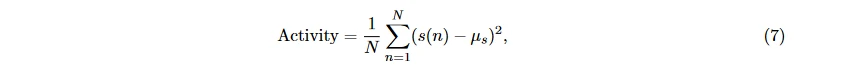
Mobility 衡量坡度的变化:
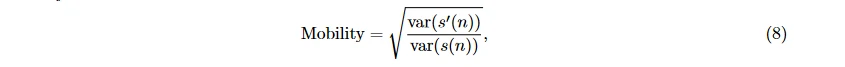
Complexity 衡量一个振幅上有多少个标准的坡 (slope):
其中, μ_s 表示信号平均值, s′(n) 表示一阶导数, var 表示方差。
高阶过零分析
Petrantonakis 等 [29] 提出高阶过零分析 (higher order crossings, HOC) 的方法, 用信号通过零点的次数来反映信号的振荡程度。将 EEG 序列 s(n) 转换为均值为 0 的序列 Z(n), n = 1, 2, . . . , N , 将该序列通过 M 个高通滤波器, k 表示滤波器的顺序, k = 1, 2, . . . , M :
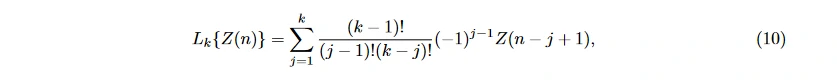
再根据 L_k{Z(n)} 构建二值序列
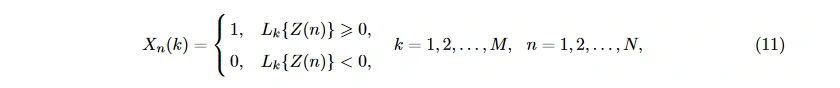
X_n(k) 中符号的变化次数即为 HOC 值:
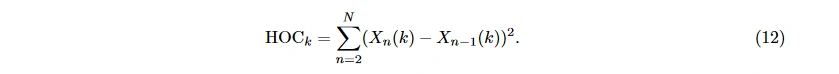
由于 EEG 在不同情绪下的振荡模式和特性不同, 与谱功率相比, HOC 可以更鲁棒地表征信号的振荡特点 [18]; 与统计特征或基于小波变换的特征相比, 使用 HOC 可以更好地区分第 1 节所述的 6 种基本情绪 [29]。
不稳定指数
不稳定指数 (non-stationary index, NSI) 衡量局部平均值随时间的变化 [26]。将信号分成 n 段并计算各段的均值, NSI 定义为这 n 个平均值的标准差。NSI 越大表示局部平均值振荡越大. Hausdorff 等[30] 发现在不同的分割时长上, 得到的 NSI 值是类似的。
分形维数
分形维数 (fractal dimension, FD) 可用来表示时域信号的复杂程度。Sevcik 方法 [31]、分形布朗运动 (fractal Brownian motion) [32]、计盒法 (box-counting) [33]、Higuchi 算法 [34] 都可用来计算 FD, 而 Higuchi 算法的效果更好 [22], 使用该算法计算 EEG 的分形维数特征 FDs 的过程如下: 首先将时域信号序列 s(n), n = 1, 2, … , N 重写为 {s(m), s(m + k), … , s(m + ⌊ (N−m)/k ⌋ · k)}, 其中, m = 1, … , k 是起始时间, k 是时间间隔。在每个 m 的取值上, 令
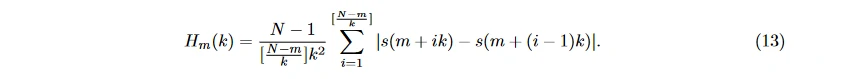
用 H(k) 表示 H_m(k) 的平均值, 取 FD_s 为
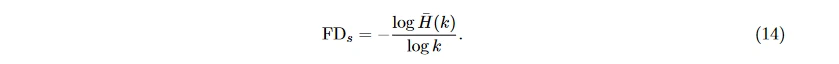
频域特征
由于时域特征无法展示信号的频率信息, 研究者加入了频域分析 [35]。首先将原始的时域信号转换至频域获得频谱, 之后将频段分解到与人的心理活动联系密切 [36] 的 5 个子频段 δ, θ, α, β, γ, 再从中计算特征。
通常使用傅里叶变换 (Fourier transfer, FT) 进行时–频域转换。将信号投影到固定的正交函数系上, 用一组变换系数 (谱线) 表示时间函数, 各谱线表示某一频率分量的相位、幅度等参数 [37]。
由于采集到的 EEG 信号为离散序列 s(n), 实际操作中多使用离散傅里叶变换法 (discrete Fourier transfer, DFT), 用求和代替积分运算, 使计算机能够处理傅里叶变换 [5]。应用于 EEG 信号可得频谱
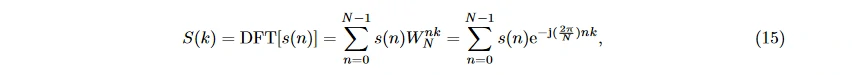
其中 k 表示样本点序号, k = 0, 1, … , N − 1。记 WN = e^[−j( 2π/N )] 为变换矩阵。从式中可看出, 每个 S(k) 需要 N − 1 次复数加法和 N 次乘法运算, 整个序列的 DFT 运算需要 N (N − 1) 次复数加法和 N^2 次复数乘法, 运算复杂度高。
快速傅里叶变换 (fast Fourier transfer, FFT) 也称库利 – 图基 (Cooley-Tukey) 算法, 利用 WN 的周期性 W^nk_N = W^[(nk) mod N]_N 和对称性 W^[nk + (N/2)]_N = −W^nk_N , 将 DFT 运算按照奇偶性逐级分解, 第 1 级将 N 个点分为各 N/2 个采样点的两组, 第 2 级再细分为各 N/4 个采样点的四组, 以此类推, 运算流程如图 3 所示, 自图的左端向右运算, 两条线的汇合点表示数值相加, 线旁标注的 W^k 表示与相应的数值相乘。例如
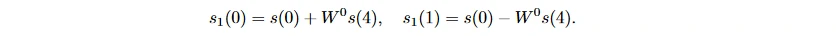
从上式可看出, 单元包含一个复数乘和两个复数加操作。对于 N 个采样点, 共 log N 层, 每层 N/2 个单元, 因而整个 FFT 算法只需要 N/2 * log N 次乘和 N * log N 次加法, 且 N 越大, FFT 的优越性越显著 [37]。
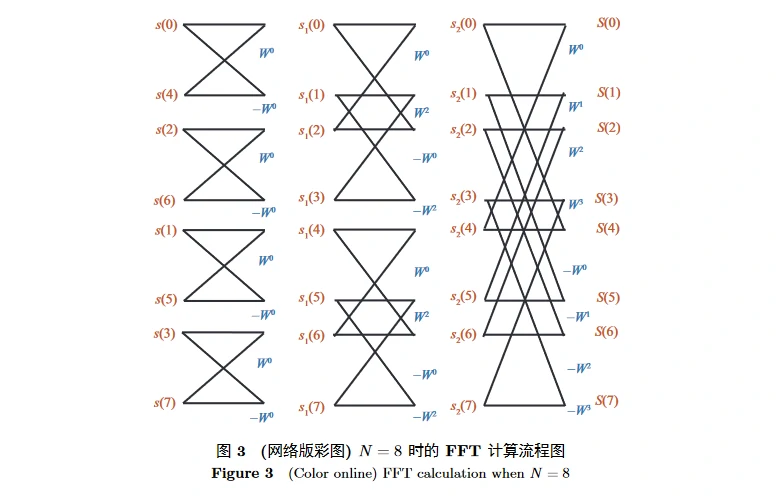
由上述步骤处理后得到的频段经过分解, 得到 5 个子频段 δ (1∼4 Hz), θ (4∼8 Hz), α (8∼12 Hz), β (13∼30 Hz), γ (31∼45 Hz), 在不同实验中, 各频段的边界略有几赫兹的差异。EEG 的不同频段与不同的意识状态有关: δ 波与无意识的状态有关, 常出现于深度无梦的睡眠; θ 波与潜意识有关, 例如有梦境的睡眠或浅度睡眠、困倦, 当诱发积极情绪时, 额中线上的 θ 波功率会增强 [38]; α 波多出现于较为放松的有意识状态, 额叶上 α 波的不对称性可反映情绪的不同效价 [39, 40]; β 波与活跃的意识状态例如注意力集中的活动有关, 在额叶区域较为显著, 可反映情绪的效价 [6, 41, 42]; γ 波则与大脑的过度活跃现象、特定的认知或运动有关 [43∼45]。中性情绪和消极情绪在 β 和 γ 波段有相似的振荡模式, 但其在 α 波段的振荡能量更高 [46]。
分解频段后, 再分别提取功率、功率谱密度、事件相关同步化、事件相关去同步化、高阶谱、微分熵等特征。
功率
功率在时域上的计算方法如式 (6) 所示。而在频域上, 可通过功率谱密度的积分运算得到。通过将整个频段划分为若干个子频段, 计算各子频段功率的平均值、最值和方差等。此外, β 波段和 α 波段的平均功率之比可以表征脑部的活跃状态, 可用于情绪识别研究 [22]。
功率谱密度
功率谱密度 (power spectral density, PSD) 描述信号的功率随频率的变化情况, 可由直接法或间接法得到。
直接法。直接法包括周期图法、Welch 法等线性经典谱估计法, 和最大熵法、最大似然法等非线性现代谱估计法。经典谱估计法更适合长序列, 当信号序列较短时, 谱分辨能力较差; 而非线性方法可保证较高的谱分辨率 [5]。
- 周期图法 (periodogram)。功率谱密度由 DFT 后幅频特性的平方除以 EEG 序列的长度得到。由于 DFT 的周期性, 功率谱也有周期性, 故称周期图。因为不同序列长度会产生不同的周期图, 无法得到稳定的估值, 故取各子区间上周期图的均值作为功率谱估值。
- Welch 法。在周期图的基础上加入平滑操作。先分成若干子波段, 再用子波段内的信号与窗函数相乘进行平滑, 最后在各子区间上取平均, 以降低周期图的波动程度。
- 最大熵法。取一组自相关函数与已知信号序列相等, 且自相关函数以外的部分随机性最大的序列, 以所取序列的功率谱作为已知序列功率谱的估值。由于要求随机性最大, 因而熵最大, 称最大熵法。
- 最大似然谱估计法。也称最小方差谱估计法。让信号通过一个滤波器, 保证所需信号不失真且其他频率信号均方差最小。若将一个确定信号加一个 Gauss 白噪声作为输入, 则滤波器输出此信号的最大似然估值, 故称为最大似然法。若信号只是一个确定信号, 例如脑电信号, 则输出为确定信号最小方差的无偏估值, 即为该信号的功率谱估值。
间接法。由维纳 – 辛钦 (Wiener-Khinchin) 定理可知, 信号的功率谱密度可由时域信号的自相关函数的傅里叶变换得到, 称为间接法。得到功率谱后, 根据给定的某一波段, 计算该波段内功率谱密度的均值、最值、方差等统计量作为特征。
事件相关 (去) 同步化
在一个刺激事件之后的若干毫秒内, EEG 信号在某一频段上功率的快速升高称为事件相关同步化 (event related synchronization, ERS); 相反, 功率降低称为事件相关去同步化 (event related desynchronization, ERD) [47]。它们在时域中不明显, 需要在频域上经过带通滤波和平滑后才能观察到。一般认为 ERS 和 ERD 与大脑神经元放电的同步性有关, 当同步性增加时能量叠加变高, 产生 ERS, 同步性下降时能量降低, 产生 ERD。第 n 个采样点上得到的特征 ERDS_n 为
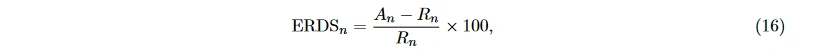
其中, A_n 表示在第 n 个采样点上的功率, R 表示在该采样点前后一段区间上的平均功率 [48]。
效价上, γ 波段上的 ERS 和 ERD 特征可区分正负性情绪 [45]; 产生正性情绪时, 颞叶左侧的 θ 波段上的 ERS 特征会变得显著, 而产生负性情绪时, 右侧 ERS 特征更显著 [41]。唤醒度上, 非中性情绪与中性情绪相比, θ 波段的 ERS 和 ERD 特征在整个右侧脑区都更加显著 [49]。
高阶谱
高阶谱 (higher order spectrum, HOS) 特征通常需要计算双谱 (bispectrum) 和双相干谱 (bicoherence)。双谱是信号三阶矩的傅里叶变换, 可用来量化信号分量之间的二次相位耦合, 即原信号与谐波发生耦合作用, 产生的新频率成分的和频与差频。与功率谱密度相比, 双谱特征涵盖相位信息, 其计算方法为
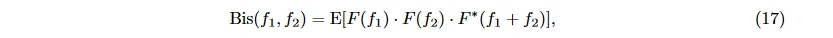
其中, f_1, f_2 指两个信号各自的频率, F(f) 指傅里叶变换, E[x] 为期望, ∗ 表示共轭复数。双相干谱是双谱的归一化形式
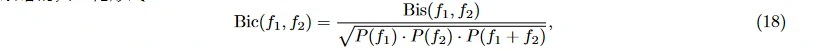
其中, P(f) = E[F(f) F∗(f)] 是功率谱。Bis 与 Bic 各自的模或模的平方都可以作为高阶谱特征 [22]。
微分熵
微分熵 (differential entropy, DE) 是香农 (Shannon) 信息熵 − ∑_x p(x) log(p(x)) 在连续变量上的推广形式
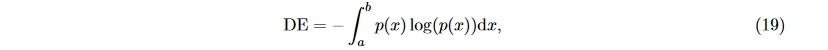
其中, p(x) 表示连续信息的概率密度函数, [a, b] 表示信息取值的区间。对于一段特定长度的近似服从 Gauss 分布 N (μ, σ^2_i ) 的 EEG, 其微分熵为 [46, 50]:
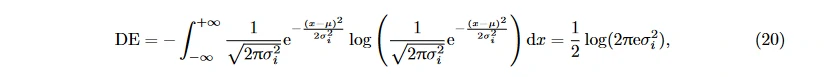
等于其在特定频段上的能量谱的对数 [51]。
Zheng 等 [46] 在识别正性、中性和负性 3 种情绪的实验中, 使用 DE 作为特征获得的识别准确率高于其他特征。
时频域特征
傅里叶变换的作用范围是整个时域, 缺乏局部化能力, 且无法确认非平稳信号各频域成分对应的时刻, 所以引入了时域与频域结合的时频域。通常做法是划分出若干时间窗, 各窗内的子信号近似平稳, 将其变换至频域得到一组频域特征, 滑动时间窗可处理不同时段, 从而同时获取信号的时域和频域信息, 提高对不稳定信号的处理能力, 可粗略计算情绪开始和持续的时间 [52]。通常使用短时傅里叶变换 (short-time Fourier transform, STFT)、小波变换 (wavelet transform, WT) 和小波包变换 (wavelet packet transform, WPT) 或 Hilbert-Huang 方法来进行时频域信号变换。
短时傅里叶变换
STFT 可提高对噪声干扰的鲁棒性 [53]。使用等长的窗函数 w(n − t) 计算窗内信号的傅里叶变换:
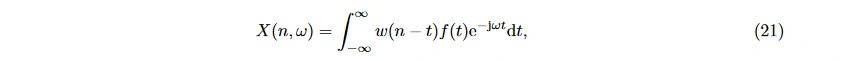
再求出各窗函数的时间点及频率成分。常见的窗函数有三角波、方波和 Gauss 函数等, 通常默认使用 Gauss 函数, 此时 STFT 也称 Gabor 转换。
选择合适的窗长度至关重要, 短的时间窗提供的信息量不足, 导致频域分辨率差; 长的时间窗又会导致各窗差异大, 时域分辨率差。目前情绪识别研究中效果好的时间窗长度多为 1 ∼ 2 s [5, 54, 55]。
小波变换
由于 STFT 的时间窗长度对效果有明显影响, 且无法同时在时域和频域获得高分辨率, 故引入小波变换。主要有两种基本类型: 连续小波变换 (continuous wavelet transform, CWT) 和离散小波变换 (discrete wavelet transform, DWT) [56]。
基本小波, 或称小波母函数 φ(t) 应平方可积, 且其傅里叶变换满足 ( |φ(ω)|2 / |ω| ) dω < ∞。平移 τ 可使小波函数在时间轴上移动; α 变大或变小会使其变窄或变宽 [57], 其中, α, τ ∈ R, α > 0。由此得到变换后的函数
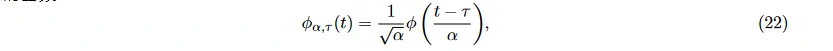
称为参数为 α 和 τ 的小波基函数。1/√α 将能量归一化。当参数可连续取值时, 称为连续小波变换; 当参数只能取离散值时, 称为离散小波变换。
小波包变换
小波变换将信号分成低频和高频两个部分, 只分解低频部分, 导致忽略表征信号细节的高频部分, 使高频分辨率差, 丢失细节信息。因此引入 WPT, 仍将信号分解为低频和高频部分, 但两部分都会继续分解, 低频上丢失的信息可以在高频中补充。因此, 小波包变换可以提供更丰富的信号分析, 提高分辨率 [58]。
Hilbert-Huang 谱
Hilbert-Huang 是一种非线性的时频域特征提取方法, 与 STFT 相比, 抵抗噪声干扰的能力更强 [22, 59]。首先用经验模式分解 (empirical mode decomposition, EMD) 得到固有模态函数 (intrinsic mode functions, IMFs) 来表征原 EEG 信号 X(t), 假设共分解出 k 个固有模态函数:
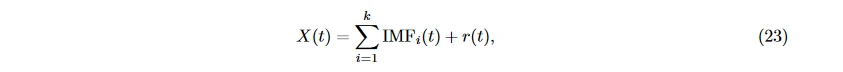
其中, r(t) 表示剩余的单调或常数的部分。再对每个 IMF_i(t) 计算 Hilbert 变换, 解析信号可用振幅 A_i(t) 和瞬时相位 θ_i(t) 来表征, 瞬时频率 f_i(t) = (1/2π) (dθ_i/dt) , 则原信号可表示为
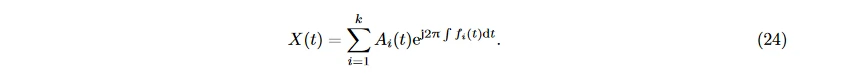
通过上述方法将 EEG 按时间段变换至频域后, 再提取如前所述的频域特征, 例如功率、功率谱密度的均值、最值等。除此之外, 也可根据时间窗提取时频域上的相对能量
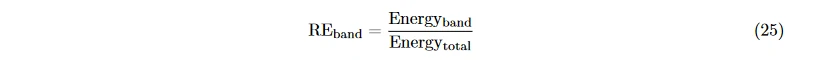
和每个时间窗上的熵
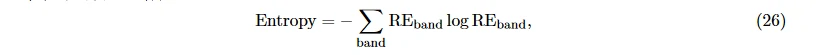
其中, Energy_band 表示某个时间窗内信号在某个频段上的能量, Energy_total 为该时间窗内所有频段能量之和 [40]。
空间域特征
脑电信号采自若干个对应大脑皮层不同位置的电极, 如前所述, 左右半球产生的 EEG 信号与情绪效价有关: 消极情绪能激活右侧额叶、颞叶和顶叶, 而积极情绪可以激活左侧区域 [60∼63]。因此形成 EEG 的空间域特征, 主要分为空频域特征和电极组合特征。
空频域
先提取各电极上的频域特征, 再用共同空间模式 (common spatial patterns, CSP) 等算法与空间域结合, 计算空频域特征。
共同空间模式。CSP 常用于二分类问题, 根据信号所属的类别标签, 设计特殊的空间滤波器, 使两类信号的功率最大, 继而得到区分度高的特征 [64, 65] 以及各电极信号的权重 [66]。
假设 n 段 EEG 信号分为正性和负性效价两类, 每段信号都表示为通道数 × 采样点个数的矩阵形式, 将两种分类下信号的协方差矩阵分别取平均得到 Σ+ 和 Σ−, 并进行特征值分解 Σ+ + Σ− = U (DU)T, U 是特征向量矩阵, D 是特征值构成的对角矩阵, 则白化值矩阵为 P = √D^−1 U T, 白化后的信号的协方差矩阵为
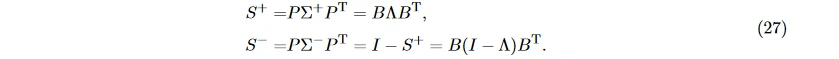
二者特征向量相同, 且特征值加和为 1。I 表示单位矩阵, B 表示特征向量矩阵, Λ 表示特征值构成的对角矩阵, 那么
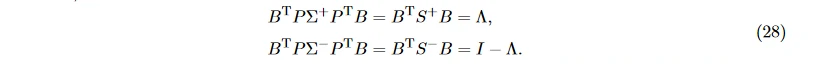
因此, 称投影矩阵 W = BTP 中的每个行向量 wj 就是一个空间滤波器, 越大的特征值表示 wj 在两类上可以得到差距越大的方差。而 W^(−1) 的每一列称为共同空间模式 [66]。
Koelstra 等 [65] 在效价 (valence)、唤醒度 (arousal) 和喜爱度 (like/dislike) 3 项上, 分别以原始 PSD 和 CSP 作为特征, 用支持向量机 (support vector machine, SVM) 进行二分类, CSP 得到的分类准确率高于 PSD。
共同空间模式的改进。由于不同个体的脑电信号在各频段上的显著程度不同, 因此当被试较多且差异较大时, 为保证识别效果, 需要大量手动调整 CSP 的频段。为了解决这一问题, Novi 等 [67] 提出子波段共同空间模式 (sub-band common spatial pattern, SBCSP), 用基于傅里叶的 Gabor 滤波器组将信号分成不同频段, 在各波段上提取 CSP 特征, 使用 LDA 算法自动选择显著的频段和相应的 CSP 特征, 最后用分类器对 CSP 特征进行分类。SBCSP 可以实现自动调整且保证识别准确率。
Ang 等 [68] 进一步改进了 SBCSP 算法, 提出了滤波器组共同空间模式 (filter bank common spatial pattern, FBCSP), 其与 SBCSP 的区别在于使用零相位切比雪夫 (Chebyshev) 滤波器组作为滤波器, 克服了 IIR (infinite impulse response) 滤波器造成的非线性相移; 在特征选择和分类中, 可广泛使用现有的特征选择和分类器算法, 具有普适性。
电极组合
计算电极组合特征时, 先对各电极信号计算前述时域、频域或时频域特征作为初步特征值, 再将若干电极组合成对, 进一步计算特征。电极对的组合方式包括对称和不对称两种, 对称方式又分为前后对称和左右对称。为了便于论述, 以 32 导 NeuroScan Quik-cap 脑电帽的电极位置为例。该设备包括 2 个参考电极和 30 个采样电极, 如图 4 所示。
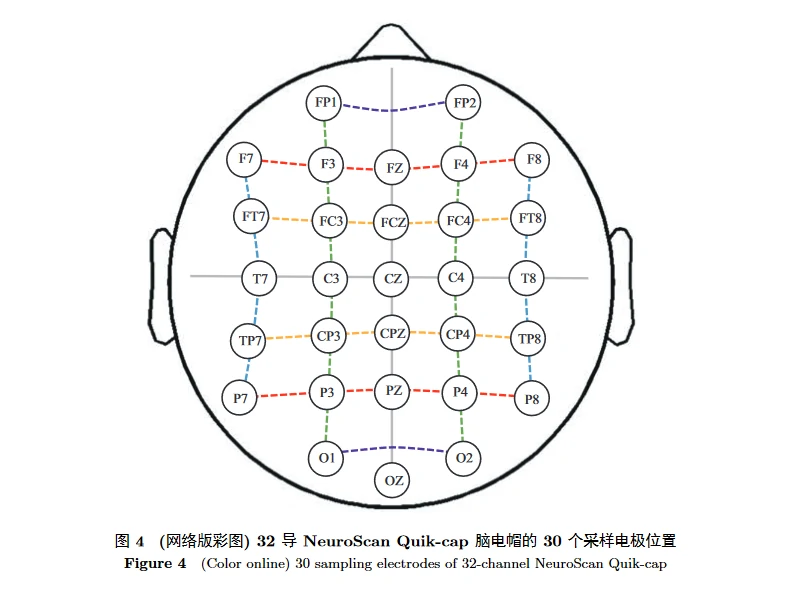
左右位置对称。以中间的灰色竖线为对称轴, 剩余 24 个电极左右对称, 可得到 12 对电极, 绿色线标识的两列电极互为电极对, 蓝色线标识的两列同理。用 L 列举出所有电极对中的左侧电极, R 为相应的右侧电极: L = {FP1, F3, FC3, C3, CP3, P3, O1, F7, FT7, T7, TP7, P7}, R = {FP2, F4, FC4, C4, CP4, P4, O2, F8, FT8, T8, TP8, P8}。
- 不对称差/不对称商。
不对称差 (differential asymmetry, DASM) 和不对称商 (rational asymmetry, RASM) 分别指左右对称电极上特征的差分和比值 [69]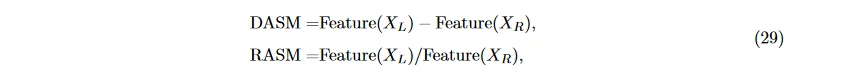
或者更复杂的计算方法, 用左右特征的差除以和, 此处称为不对称系数 [18]: 
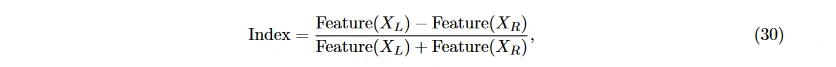其中, X_L 和 X_R 分别表示左侧和右侧电极采集到的 EEG 信号, Feature(X) 表示在信号 X 上提取的初步特征值。 - 多维度有向信息。
Sakata 等 [70] 提出了多维度有向信息 (multidimensional directed information, MDI), 反映从某个电极流向其他电极的信息量, 通常测量左右电极对之间流动的信息量。MDI 的优势在于可以表示各电极之间信号量的绝对量而非相对量 [71]。首先将两个电极上长度为 N 的 EEG 信号平均划分为 n 段, 每段以 xk 和 yk 界定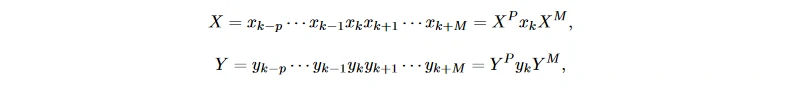
那么两序列的互信息为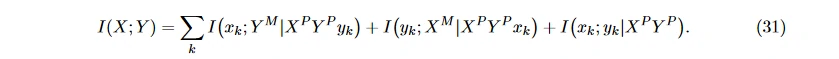 
前后位置对称。以图 4 中间横向的灰色横线为对称轴, 并舍弃 OZ 电极, 剩余 24 个电极前后对称, 可得到 12 对电极, 紫色线标识的两行电极互为电极对, 红色线、橙色线同理。用 F 列举出所有电极对中的前部电极, P 为相应的后部电极: F = {FP1, FP2, F7, F3, FZ, F4, F8, FT7, FC3, FCZ, FC4, FT8}, P = {O1, O2, P7, P3, PZ, P4, P8, TP7, CP3, CPZ, CP4, TP8}。
DCAU (differential caudality) 可以用来描述前后电极上的不对称性 [46]
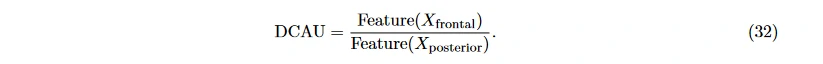
不同脑电特征对于情绪识别结果的影响
为了测试特征对情绪识别结果的贡献, 本文选择 3 个脑电数据库 SEED, DREAMER 和 CASTHU, 计算各类特征值, 将稀疏线性判别分析 (sparse linear discriminant analysis, SLDA) [72] 选择特征的权重作为评价标准。
需要说明的是, 频域与时频域本质都是将时域信号变换至频域, 且二者计算的特征类型 (如 PSD, 微分熵等) 相同; 但时频域按时间段划分信号, 含有更丰富的特征信息, 也更常用于情绪识别领域。因而本实验对 EEG 加时间窗以提取时频域特征, 不计算整个信号的频域特征。
数据库介绍
SEED
SEED 数据库 [46, 69] 由上海交通大学发布, 用时长 4 min 左右的华语电影片段诱发正性、中性和负性效价的 3 种情绪。使用 62 导的 ESI NeuroScan 系统采集 15 名被试 (7 名男性, 8 名女性, 年龄平均值为 23.27, 标准差为 2.37) 的脑电数据, 采样率为 1000 Hz。每名被试在不同时间做 3 次实验, 每次观看 15 段电影片段, 即共 45 个试次。对 EEG 信号的预处理包括: 信号下采样至 200 Hz, 去除眼电和肌电噪声, 并使用 0.3 ∼ 50 Hz 的带通滤波器。计算时频域特征时, 使用长度为 1 s 互不重叠的 hanning 窗进行短时傅里叶变换, 并划分 5 个频段 δ (1∼3 Hz), θ (4∼7 Hz), α (8∼13 Hz), β (14∼30 Hz), γ (31∼50 Hz)。
DREAMER
DREAMER 数据库 [73] 由 University of the West of Scotland 发布, 提供被试对影片在效价、唤醒度和控制度上的评分, 并据此得到相应情绪的正负性或唤醒度、控制度的高低。影片共 18 段, 长度在 65 ∼ 393 s 之间 [73, 74]。实验使用 14 导的 Emotiv EPOC 系统, 采集 23 名被试 (14 名男性, 9 名女性, 年龄平均值为 26.6, 标准差为 2.7) 观看电影时的脑电和心电数据, 采样率为 128 Hz。截取每段信号最后的 60 s, 并用 MATLAB 环境下的 EEGLAB 工具包 [75] 做预处理。用长度为 2 s、相邻窗重叠 1 s 的时间窗进行短时傅里叶变换, 并将信号分为 θ (4∼7 Hz), α (8∼13 Hz), β (14∼30 Hz) 3 个频段。
CAS-THU
CAS-THU 数据库[76] 由中国科学院心理研究所与清华大学共同提出, 使用 16 段华语影片诱发 8 种离散情绪, 包括搞笑、高兴和温馨 3 种正性情绪, 厌恶、恐惧、愤怒和悲伤 4 种负性情绪以及中性状态。使用 14 导 Emotiv EPOC 系统采集 30 名男性被试 (年龄平均值为 23, 标准差为 1.73) 的脑电数据。预处理时先通过 1 ∼ 45 Hz 的带通滤波器, 再用独立成分分析 (independent component analysis, ICA) 和 MATLAB 环境下的 EEGLAB 工具包 [75] 除去眼电干扰。与 DREAMER 相同, 采用长度 2 s 且相邻重叠 1 s 的时间窗做 STFT, 将信号划分为 5 个频段: δ (1∼4 Hz), θ (4∼8 Hz), α (8∼12 Hz), β (13∼30 Hz), γ (31∼45 Hz) [76]。
综上可知, 3 个数据库都包含情绪的效价信息, 其中 SEED 和 CAS-THU 包含正性、中性和负性 3 类效价, DREAMER 只包含正性和负性两类效价, 所以本实验只衡量各特征在判断效价上的作用。
特征提取
由于 ERP, ERS 和 ERD 3 项事件相关的特征需要离散材料作为诱发, 而本实验数据库均用视频持续诱发情绪, 更符合实际应用场景。因此在本文的实验中, 不提取这 3 个特征。另外, CSP 适用于二分类任务, 因此只对 DREAMER 数据库计算 CSP 特征。综上, 本文实验在 3 个数据库上共同计算的特征包括:
- 时域。平均值、标准差、一阶差分、归一化的一阶差分、二阶差分、归一化的二阶差分、Hjorth 特征 (activity, mobility, complexity)、能量、功率、高阶过零分析、不稳定指数、Higuchi 分形维数。
- 时频域。功率谱密度、高阶谱、微分熵。
- 空间域。DASM、RASM、不对称系数、DCAU、多维度有向信息。
对于每个数据库, 按照其描述添加相应时间窗应用 STFT。需要注意的是, 在计算高阶谱 HOS 特征时, 我们使用 MATLAB 上的 HOSA 工具包 [77]; 在提取电极组合特征时, 使用广泛用于情绪识别领域的 PSD 特征。
表 1 列出了 3 个数据集上各类特征的维数, 需要强调的是, 每类特征会有多列, 即 “一类” 特征可能包含 “多维” 特征值。
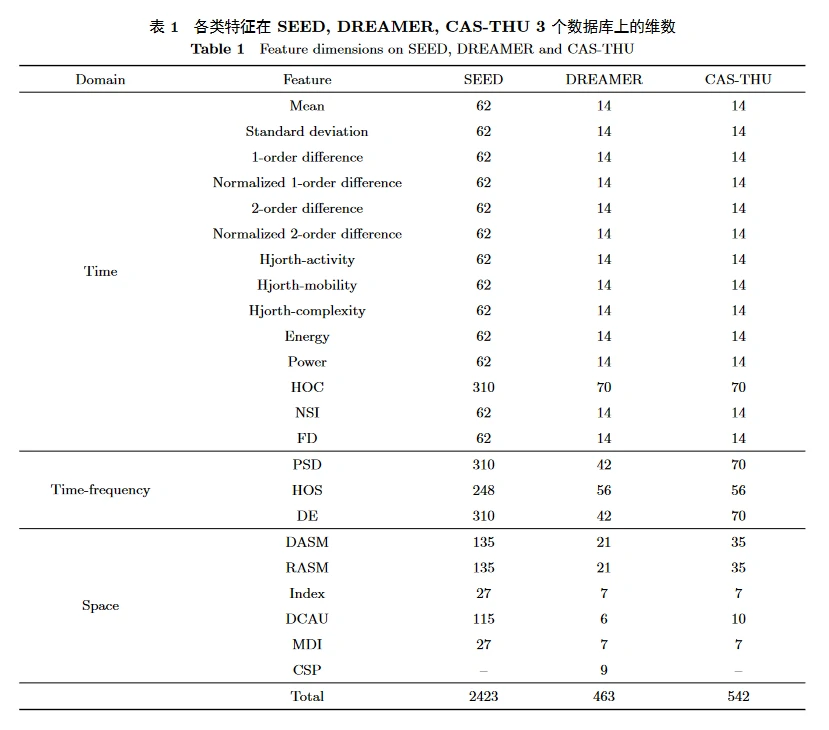
计算特征重要程度
令 n×p 的矩阵 X 表示提取的 EEG 特征, n 表示样本数, 每一行样本都属于一类效价。属于第 j 类的样本下标为 C_j, 数量为 n_j; p 为特征维数, 即表 1 最后一行的 “总计” 维数, 例如 pSEED = 2423。线性判别分析 (linear discriminant analysis, LDA) 从 Fisher 线性判别法的角度寻找判别向量, 使类间方差相对类内方差最大化, 即
但是, 当所选特征的数量大于观测数量时, 特征的类内协方差矩阵会变得单一。可应用稀疏的 LDA (sparse LDA, SLDA) [72], 添加 l1 罚项对判别向量施加稀疏约束, 以解决这个问题。
在本实验中, 用 MATLAB 上的 SpaSM 工具包 [78] 实现 SLDA 算法, 使用默认参数以保证算法在不同数据库上的统一性。采用准确率较高的被试留一法划分数据, 即, 若数据集中包括 s 名被试, 将其划分为 s 个子集, 各子集包含一个被试的全部样本 [79]。每次取其中的 s − 1 个子集的数据送入SLDA 算法, 计算权重 Wi; 在 s 次上取权重均值并排序, 再计算每一类特征的 “重要程度”, “重要程度” 定义如下：
定义1 (重要程度) 若某特征共有 p_i 维, 其中有 m_i 维排在所有维度的前 x%, 则该特征的重要程度值为
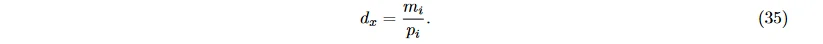
例如, 由表 1 可知, pSEED = 2423, 其中 310 列是功率谱密度 (PSD), 令 x = 10, 则关注权重排在前 2423 × 10% ≈ 242 位的特征, 若 242 列中有 100 列来自 PSD, 则 PSD 特征的重要程度值 d_10 = 100/310 ≈ 0.32。x 值越小, 越可以反映特征的重要程度。
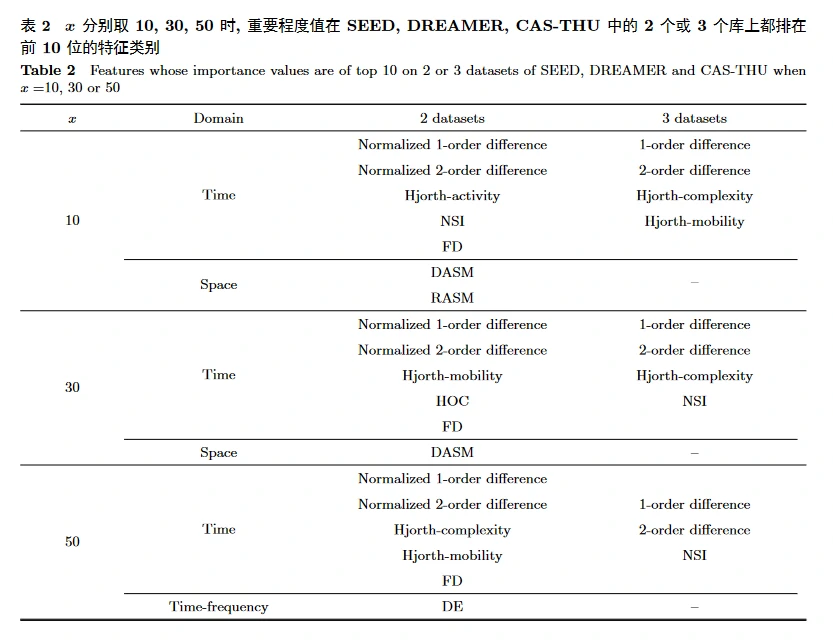
结果分析和讨论
将各类特征按照 x = 10, 30, 50 分别计算重要程度并排序; 统计在 2 个或全部 3 个数据库上都排在前 10 位的特征。需要注意的是, CSP 为 DREAMER 数据集独有的特征, 故不参与排名。最终结果如表 2 所示。可看出时域特征中的一阶差分、二阶差分、Hjorth 特征, 以及不稳定指数的重要程度最高, 其次是归一化的一阶差分、归一化的二阶差分, 以及分形维数; 频域中的微分熵, 空间域中的 DASM 和 RASM 也有较好的表现。时域特征对效价的分辨能力强于时频域和空间域。
对于 CSP 特征, 当 x 取 10 时, 其重要程度排在 DREAMER 所有 23 类特征中的第 16 位; 当 x 取 30 时, 排在第 5 位; x 取 50 时排在第 2 位。说明 CSP 在该数据库上可以较好地表征效价, 但表征能力并不突出。
根据以上结果可知, 时域特征对情绪效价的分辨能力最强, 因而在后续相关研究中, 研究者可考虑加入时域特征来优化情绪识别效果。此外在所有时域特征中, 统计特征的重要程度高, 原因之一在于, 不同数据库中同效价的影片唤醒度可能有异。例如诱发正性情绪的两部影片, 其产生正性情绪的强烈程度可能不同, 即此处效价的分类会受到唤醒度的影响。
对未来工作的展望
实际应用
需要建立包括脑电信号数据和情绪诱发材料的情绪标准化库, 作为后续情绪理论研究的基础。该库应满足以下要求:
- 采用视听刺激的方式诱发情绪。相比于单一的视觉或听觉刺激, 视听刺激结合的方式更贴近实际生活, 内容和情节也更丰富, 例如电影片段、音乐视频等, 这种方式下产生的脑电信号具有良好的动态性、不可欺骗性和高生态效度 [80]。
- 适用于中国社会和文化背景。由于文化背景的差异, 现有国外标准库难以直接用于我国被试, 因此建立针对我国人群的标准库具有极大的应用价值。
- 涵盖更多的正性情绪类别及样本数。近年来有关情绪的最新行为学研究认为, 积极情绪至少可以分为 10 种代表性类型 [81], 包括高兴、感恩、宁静、兴趣、希望、自豪、搞笑、激励、敬畏、爱。在实践应用或社会需求的角度, 积极情绪比消极情绪更重要。积极情绪有助于扩大注意、认知及行为的范围, 促进身体、智力与社交能力的健康发展。但已有情绪库中的正性情绪种类较少, 正负情绪材料和样本数量不平衡, 不利于情绪模型建立和应用, 因此脑电信号数据库应涵盖更多的正性情绪种类及样本数。
- 尽量排除刺激材料本身对被试的影响。应尽量排除刺激材料本身内容 (如画面的明暗、声音的强弱等) 产生的影响, 让采集的 EEG 信号直接反映情绪对被试的影响。
理论研究
- 从多学科交叉角度分析脑电特征与情绪识别结果的关系。基于 EEG 信号的情绪识别是多学科交叉的研究问题. 而现有的情绪识别研究中, 特征计算方法多来自电信号处理领域, 对特征的讨论主要停留在实验准确率的层面, 鲜有特征与情绪本身联系的探讨. 如果从生理、心理和神经科学的理论层面分析特征与情绪的关系, 将有助于理解情绪产生的机制, 进而设计出与情绪最相关的脑电特征, 优化识别效果。
- 多人脑功能影像数据联合分析方法。通过联合分析多名被试在特定任务状态下大脑活动之间的关系, 研究被试在完成任务时的认知过程, 可提取绝对强度不大, 但持续时间较长、个体间一致性较好的 “微弱” 神经响应. 这一方法可能分析出在传统事件相关分析中被低估的神经响应, 有利于提取更深层次的情绪响应特性。
- 深度学习方法。近年来兴起的深度学习 (deep learning) 方法采用分层结构, 先将原空间的特征表示转换到新的空间, 再进行后续分类。与人工构造的特征相比, 利用海量数据学习到的特征更能反映数据的内在本质 [82], 克服特征冗余问题, 提高情绪识别的智能和普适性。
总结
情绪识别是人机交互中的重要组成部分, 在医学、教育和军事等方面都具有切实的研究需要和广阔的应用前景, 脑电信号是目前情绪识别领域中识别效果较好的生理指标. 从信号中提取与情绪关联度高、区分度大的特征有助于达到较高的情绪识别准确率。
本文围绕面向情绪识别的脑电特征, 从时域、频域、时频域和空间域 4 个方面介绍了特征的定义、计算方法和与情绪的联系, 在总结已有工作的基础上, 在 SEED, DREAMER 和 CAS-THU 3 个公开的脑电 – 情绪数据集上, 对各类特征的效价区分能力进行评估和比较, 并展望未来可行的研究方向, 为开展进一步研究提供思路。
参考文献
[1] Huang X T. Introduction to Psychology. Beijing: Peoples Education Press, 1991 [黄希庭. 心理学导论. 北京: 人民教育出版社, 1991]
[2] van den Broek E L. Ubiquitous emotion-aware computing. Pers Ubiquit Comput, 2013, 17: 53–67
[3] Posner J, Russell J A, Peterson B S. The circumplex model of affect: an integrative approach to affective neuroscience, cognitive development, and psychopathology. Develop Psychopathol, 2005, 17: 715–734
[4] Lang P J. The emotion probe: studies of motivation and attention. Am Psychol, 1995, 50: 372–385
[5] Zhao G Z, Song J J, Ge Y, et al. Advances in emotion recognition based on physiological big data. J Comput Res Dev, 2016, 53: 80–92 [赵国朕, 宋金晶, 葛燕, 等. 基于生理大数据的情绪识别研究进展. 计算机研究与发展, 2016, 53: 80–92]
[6] Alarcao S M, Fonseca M J. Emotions recognition using EEG signals: a survey. IEEE Trans Affect Comput, 2017. doi: 10.1109/TAFFC.2017.2714671
[7] Chanel G, Kierkels J J M, Soleymani M, et al. Short-term emotion assessment in a recall paradigm. Int J HumanComput Stud, 2009, 67: 607–627
[8] Hruby T, Marsalek P. Event-related potentials-the P3 wave. Acta Neurobiol Exp, 2002, 63: 55–63
[9] Luck S J, Kappenman E S. The Oxford Handbook of Event-Related Potential Components. Oxford: Oxford University Press, 2011
[10] Lithari C, Frantzidis C A, Papadelis C, et al. Are females more responsive to emotional stimuli? A neurophysiological study across arousal and valence dimensions. Brain Topogr, 2010, 23: 27–40
[11] Yazdani A, Lee J S, Ebrahimi T. Implicit emotional tagging of multimedia using EEG signals and brain computer interface. In: Proceedings of the 1st SIGMM Workshop on Social Media, Beijing, 2009. 81–88
[12] Codispoti M, Ferrari V, Bradley M M. Repetition and event-related potentials: distinguishing early and late processes in affective picture perception. J Cogn Neurosci, 2007, 19: 577–586
[13] Olofsson J K, Nordin S, Sequeira H, et al. Affective picture processing: an integrative review of ERP findings. Biol Psychol, 2008, 77: 247–265
[14] Olofsson J K, Polich J. Affective visual event-related potentials: arousal, repetition, and time-on-task. Biol Psychol, 2007, 75: 101–108
[15] Gianotti L R R, Faber P L, Schuler M, et al. First valence, then arousal: the temporal dynamics of brain electric activity evoked by emotional stimuli. Brain Topogr, 2008, 20: 143–156
[16] Jiang J F, Zeng Y, Tong L, et al. Single-trial ERP detecting for emotion recognition. In: Proceedings of the 17th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Shanghai, 2016. 105–108
[17] Smith N K, Cacioppo J T, Larsen J T, et al. May I have your attention, please: electrocortical responses to positive and negative stimuli. Neuropsychologia, 2003, 41: 171–183
[18] Kim M K, Kim M, Oh E, et al. A review on the computational methods for emotional state estimation from the human EEG. Comput Math Method Med, 2013, 2013: 13
[19] Bernat E, Bunce S, Shevrin H. Event-related brain potentials differentiate positive and negative mood adjectives during both supraliminal and subliminal visual processing. Int J Psychophysiol, 2001, 42: 11–34
[20] Cuthbert B N, Schupp H T, Bradley M M, et al. Brain potentials in affective picture processing: covariation with autonomic arousal and affective report. Biol Psychol, 2000, 52: 95–111
[21] Nieuwenhuis S, Aston-Jones G, Cohen J D. Decision making, the P3, and the locus coeruleus-norepinephrine system. Psychol Bull, 2005, 131: 510–532
[22] Jenke R, Peer A, Buss M. Feature extraction and selection for emotion recognition from EEG. IEEE Trans Affect Comput, 2014, 5: 327–339
[23] Wang X W, Nie D, Lu B L. EEG-based emotion recognition using frequency domain features and support vector machines. In: Proceedings of International Conference on Neural Information Processing, Berlin, 2011. 734–743
[24] Bastos-Filho T F, Ferreira A, Atencio A C, et al. Evaluation of feature extraction techniques in emotional state recognition. In: Proceedings of the 4th International Conference on Intelligent Human Computer Interaction (IHCI), Kharagpur, 2012
[25] Picard R W, Vyzas E, Healey J. Toward machine emotional intelligence: analysis of affective physiological state. IEEE Trans Pattern Anal Mach Intell, 2001, 23: 1175–1191
[26] Kroupi E, Yazdani A, Ebrahimi T. EEG correlates of different emotional states elicited during watching music videos. In: Proceedings of Affective Computing and Intelligent Interaction, Berlin, 2011. 457–466
[27] Fan C X, Cao L N. Communication Principle. Beijing: National Defense Industrial Press, 2001 [樊昌信, 曹丽娜. 通信原理. 北京: 国防工业出版社, 2001]
[28] Hjorth B. EEG analysis based on time domain properties. Electroencephal Clin Neurophysiol, 1970, 29: 306–310
[29] Petrantonakis P C, Hadjileontiadis L J. Emotion recognition from EEG using higher order crossings. IEEE Trans Inform Technol Biomed, 2010, 14: 186–197
[30] Hausdorff J M, Lertratanakul A, Cudkowicz M E, et al. Dynamic markers of altered gait rhythm in amyotrophic lateral sclerosis. J Appl Physiol, 2000, 88: 2045–2053
[31] Ansari-Asl K, Chanel G, Pun T. A channel selection method for EEG classification in emotion assessment based on synchronization likelihood. In: Proceedings of the 15th European Signal Processing Conference, Poznan, 2007. 1241–1245
[32] Khosrowabadi R, bin Abdul Rahman A W. Classification of EEG correlates on emotion using features from Gaussian mixtures of EEG spectrogram. In: Proceeding of the 3rd International Conference on Information and Communication Technology for the Moslem World (ICT4M), Jakarta, 2010. 102–107
[33] Sourina O, Liu Y S. A fractal-based algorithm of emotion recognition from EEG using arousal-valence model. In: Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2011), Rome, 2011. 209–214
[34] Liu Y, Sourina O. Real-time fractal-based valence level recognition from EEG. In: Proceedings of Transactions on Computational Science XVIII, Berlin, 2013. 101–120
[35] Conneau A C, Essid S. Assessment of new spectral features for eeg-based emotion recognition. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, 2014. 4698–4702
[36] Nie D, Wang X W, Duan R N, et al. A survey on EEG based emotion recognition. Chinese J Biomed Eng, 2012, 31: 595–606 [聂聃, 王晓韡, 段若男, 等. 基于脑电的情绪识别研究综述. 中国生物医学工程学报, 2012, 31: 595–606]
[37] Zheng J L, Ying Q H, Yang W L. Signal and System. 2nd ed. Beijing: Higher Education Press, 2000 [郑君里, 应启珩, 杨为理. 信号与系统 (第二版). 北京: 高等教育出版社, 2000]
[38] Sammler D, Grigutsch M, Fritz T, et al. Music and emotion: electrophysiological correlates of the processing of pleasant and unpleasant music. Psychophysiology, 2007, 44: 293–304
[39] Davidson R J. What does the prefrontal cortex “do” in affect: perspectives on frontal EEG asymmetry research. Biol Psychology, 2004, 67: 219–234
[40] Yuvaraj R, Murugappan M, Ibrahim N M, et al. Optimal set of EEG features for emotional state classification and trajectory visualization in Parkinson’s disease. Int J Psychophysiol, 2014, 94: 482–495
[41] Aftanas L I, Varlamov A A, Pavlov S V, et al. Affective picture processing: event-related synchronization within individually defined human theta band is modulated by valence dimension. Neurosci Lett, 2001, 303: 115–118
[42] Yuvaraj R, Murugappan M, Ibrahim N M, et al. Emotion classification in Parkinson’s disease by higher-order spectra and power spectrum features using EEG signals: a comparative study. J Integr Neurosci, 2014, 13: 89–120
[43] Keil A, M ̈ uller M M, Gruber T, et al. Effects of emotional arousal in the cerebral hemispheres: a study of oscillatory brain activity and event-related potentials. Clin Neurophysiol, 2001, 112: 2057–2068
[44] Bos D O. EEG-based emotion recognition-the influence of visual and auditory stimuli. Emotion, 2007, 57: 1798–1806
[45] Balconi M, Lucchiari C. Consciousness and arousal effects on emotional face processing as revealed by brain oscillations. A gamma band analysis. Int J Psychophysiol, 2008, 67: 41–46
[46] Zheng W L, Lu B L. Investigating critical frequency bands and channels for EEG-based emotion recognition with deep neural networks. IEEE Trans Auton Mental Dev, 2015, 7: 162–175
[47] Bekkedal M Y V, Rossi III J, Panksepp J. Human brain EEG indices of emotions: delineating responses to affective vocalizations by measuring frontal theta event-related synchronization. Neurosci Biobehaval Rev, 2011, 35: 1959–1970
[48] Graimann B, Pfurtscheller G. Quantification and visualization of event-related changes in oscillatory brain activity in the time-frequency domain. Progress Brain Res, 2006, 159: 79–97
[49] Balconi M, Lucchiari C. EEG correlates (event-related desynchronization) of emotional face elaboration: a temporal analysis. Neurosci Lett, 2006, 392: 118–123
[50] Duan R N, Zhu J Y, Lu B L. Differential entropy feature for EEG-based emotion classification. In: Proceedings of the 6th International IEEE/EMBS Conference on Neural Engineering (NER), San Diego, 2013. 81–84
[51] Shi L C, Jiao Y Y, Lu B L. Differential entropy feature for EEG-based vigilance estimation. In: Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, 2013. 6627–6630
[52] Behnam H, Sheikhani A, Mohammadi M R, et al. Analyses of EEG background activity in Autism disorders with fast Fourier transform and short time Fourier measure. In: Proceedings of International Conference on Intelligent and Advanced Systems, Kuala Lumpur, 2007. 1240–1244
[53] Kıymık M K, Guler I, Dizibuyuk A, et al. Comparison of STFT and wavelet transform methods in determining epileptic seizure activity in EEG signals for real-time application. Comput Biol Med, 2005, 35: 603–616
[54] Yoon H J, Chung S Y. EEG-based emotion estimation using Bayesian weighted-log-posterior function and perceptron convergence algorithm. Comput Biol Med, 2013, 43: 2230–2237
[55] RozgicV, Vitaladevuni S N, Prasad R. Robust EEG emotion classification using segment level decision fusion. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, 2013. 1286–1290
[56] Akin M. Comparison of wavelet transform and FFT methods in the analysis of EEG signals. J Med Syst, 2002, 26: 241–247
[57] Adeli H, Zhou Z, Dadmehr N. Analysis of EEG records in an epileptic patient using wavelet transform. J Neurosci Method, 2003, 123: 69–87
[58] Sun Z, Chang C C. Structural damage assessment based on wavelet packet transform. J Struct Eng, 2002, 128: 1354–1361
[59] Hadjidimitriou S K, Hadjileontiadis L J. Toward an EEG-based recognition of music liking using time-frequency analysis. IEEE Trans Biomed Eng, 2012, 59: 3498–3510
[60] Davidson R J, Ekman P, Saron C D, et al. Approach-withdrawal and cerebral asymmetry: emotional expression and brain physiology: I. J Personality Soc Psychol, 1990, 58: 330–341
[61] Huang D, Guan C, Ang K K, et al. Asymmetric spatial pattern for EEG-based emotion detection. In: Proceedings of International Joint Conference on Neural Networks (IJCNN), Brisbane, 2012
[62] Takahashi K. Remarks on emotion recognition from bio-potential signals. In: Proceedings of IEEE International Conference on Industrial Technology (IEEE ICIT’04), Hammamet, 2004. 1148–1153
[63] Davidson R, Fox N. Asymmetrical brain activity discriminates between positive and negative affective stimuli in human infants. Science, 1982, 218: 1235–1237
[64] Blankertz B, Tomioka R, Lemm S, et al. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal Process Mag, 2008, 25: 41–56
[65] Koelstra S, Yazdani A, Soleymani M, et al. Single trial classification of EEG and peripheral physiological signals for recognition of emotions induced by music videos. In: Proceedings of International Conference on Brain Informatics, Berlin, 2010. 89–100
[66] Winkler I, J ̈ager M, Mihajlovic V, et al. Frontal EEG asymmetry based classification of emotional valence using common spatial patterns. World Acad Sci Eng Technol, 2010, 45: 373–378
[67] Novi Q, Guan C, Dat T H, et al. Sub-band common spatial pattern (SBCSP) for brain-computer interface. In: Proceedings of the 3rd International IEEE/EMBS Conference on Neural Engineering, Kohala Coast, 2007. 204–207
[68] Ang K K, Chin Z Y, Zhang H, et al. Filter bank common spatial pattern (FBCSP) in brain-computer interface. In: Proceedings of IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, 2008. 2390–2397
[69] Duan R N, Wang X W, Lu B L. EEG-based emotion recognition in listening music by using support vector machine and linear dynamic system. In: Proceedings of International Conference on Neural Information Processing, Berlin, 2012. 468–475
[70] Sakata O, Shiina T, Saito Y. Multidimensional directed information and its application. Electron Commum Jpn, 2002, 85: 45–55
[71] Petrantonakis P C, Hadjileontiadis L J. A novel emotion elicitation index using frontal brain asymmetry for enhanced EEG-based emotion recognition. IEEE Trans Inform Technol Biomed, 2011, 15: 737–746
[72] Clemmensen L, Hastie T, Witten D, et al. Sparse discriminant analysis. Technometrics, 2011, 53: 406–413
[73] Katsigiannis S, Ramzan N. DREAMER: a database for emotion recognition through EEG and ECG signals from wireless low-cost off-the-shelf devices. IEEE J Biomed Health Inform, 2018, 22: 98–107
[74] Song T F, Zheng W M, Song P, et al. EEG emotion recognition using dynamical graph convolutional neural networks. IEEE Trans Affect Comput, 2018. doi: 10.1109/TAFFC.2018.2817622
[75] Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods, 2004, 134: 9–21
[76] Liu Y J, Yu M, Zhao G, et al. Real-time movie-induced discrete emotion recognition from EEG signals. IEEE Trans Affect Comput, 2018, 9: 550–562
[77] Swami A, Mendel C, Nikias C. Higher-order spectral analysis (HOSA) toolbox. Version, 2000, 2: 3
[78] Sjostrand K, Clemmensen L H, Larsen R, et al. SpaSM: a matlab toolbox for sparse statistical modeling. J Stat Soft, 2018, 84: 37
[79] Zhou Z H. Machine Learning. Beijing: Tsinghua University Press, 2016 [周志华. 机器学习. 北京: 清华大学出版社, 2016]
[80] Gross J J, Levenson R W. Emotion elicitation using films. Cogn Emotion, 1995, 9: 87–108
[81] Fredrickson B L. Positive emotions and upward spirals in organizations. Positive Organ Scholarship, 2003, 3: 163–175
[82] Yu C, Sun K, Zhong M Y, et al. One-dimensional handwriting: inputting letters and words on smart glasses. In: Proceedings of CHI Conference on Human Factors in Computing Systems (CHI’16), San Jose, 2016. 71–82
原文链接
原文
引用：张冠华, 余旻婧, 陈果, 等. 面向情绪识别的脑电特征研究综述. 中国科学: 信息科学, 2019, doi: 10.1360/N112018-00337 Zhang G H, Yu M J, Chen G, et al. A review of EEG features for emotion recognition (in Chinese). Sci Sin Inform, 2019, doi: 10.1360/N112018-00337
Reference: Guanhua ZHANG, Minjing YU, Guo CHEN, Yiheng HAN, Dan ZHANG, Guozhen ZHAO, Yong-Jin LIU, A review of EEG features for emotion recognition, In Journal of SCIENTIA SINICA Informationis, Volume 49, Issue 9, 2019, Pages 1097-1118, ISSN 1674-7267, https://doi.org/10.1360/N112018-00337.