- CS231n - Loss Functions and Optimization
损失函数–Loss Function– SVM
损失函数模型:
- 对于N张图片的数据集:其中xi是第i个图像,yi是对应的第i个标签
- 损失函数应该是每一张图片的损失函数之和,可以用下面的公式来表示:
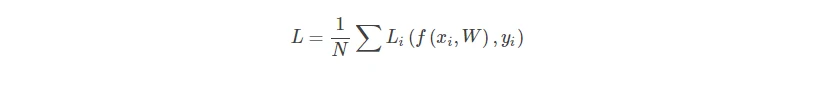
在得到score之后,可以使用多分类线性SVM
- 对于xi,yi,令s=f(xi,W),那么SVM可以表示为:
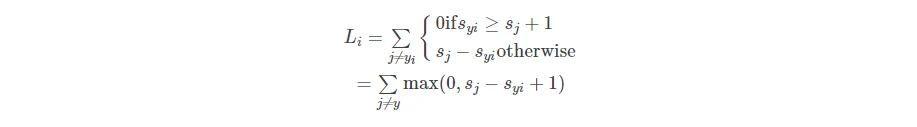 其中syi代表的是第i张图像正确标签分类所在的scores对应的列,yi对应的值在scores列中对应的C类相同
其中syi代表的是第i张图像正确标签分类所在的scores对应的列,yi对应的值在scores列中对应的C类相同
syi≥sj+1的含义是正确的分类要比错误分类的score大1,该项贡献的损失函数为0;反之损失函数正值 - 详细的一列的计算过程如下,在作业中使用循环和向量化(vectorization)两种,计算方法很巧妙,这里使用循环的理解方式:
 对于将猫和青蛙分类错误的情况下,得分较低的损失函数较大;在车的分类中,得分越高的损失函数值较小;而对于一种最理想的情况,正确分类为1,而其他的分类为0,那么损失函数将为0
对于将猫和青蛙分类错误的情况下,得分较低的损失函数较大;在车的分类中,得分越高的损失函数值较小;而对于一种最理想的情况,正确分类为1,而其他的分类为0,那么损失函数将为0 - 而最后的损失函数由以下公式得到:
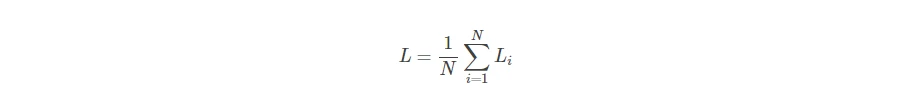
- Q1:而对于car分类的值如果有微小改变,在正确的值始终比错误的值大1的情况,损失函数不变;但当差值小于1的时候,损失函数值增大。因此微小改变一般不会对损失函数值产生影响。
- Q2:最小的损失函数值为0,最大的损失函数值为无穷大
- Q3:当W初始值很小,所有的s都近似为0的时候,损失函数的值最终为1
- Q4:当算上正确分类的一行时,那么最终的损失函数趋近1,对于整个训练过程没有影响。
- Q5:使用平均和使用和没有太大区别,只是比例不同
- Q6: 如果使用以下均方函数,不会对结果产生太大的影响。
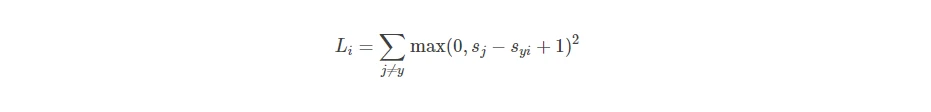
- 对于xi,yi,令s=f(xi,W),那么SVM可以表示为:
正则化(regularization)——防止过拟合,引入W的作用
- 正则化的概念:在特征参数维度较大、训练样本较少情况下,会导致模型过拟合。一方面可以通过丢掉某些参数(dropout等);另一方法需要加入正则项对特征参数进行惩罚,降低特征参数的影响,通常如下:
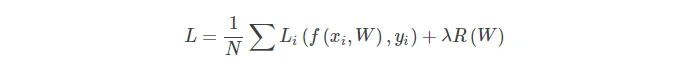 其中公式中 λ 为平衡两者之间的影响,但通常值较大,数量级在10^4以上。
其中公式中 λ 为平衡两者之间的影响,但通常值较大,数量级在10^4以上。
正则化详细地讲解参照网页:https://www.cnblogs.com/jianxinzhou/p/4083921.html - 欧卡姆剃刀:“Among competing hypotheses,the simplest is the best” William of Ockham, 1285 - 1347
- 正则化的方法(直接贴图):

- L2正则化(权重衰减):对于使得损失函数相同的特征参数矩阵,优选特征参数矩阵均匀的,[0.25, 0.25, 0.25, 0.25]优于[1, 0, 0, 0]
- L1正则化(稀疏特性):具体还未讲到。
- 正则化的概念:在特征参数维度较大、训练样本较少情况下,会导致模型过拟合。一方面可以通过丢掉某些参数(dropout等);另一方法需要加入正则项对特征参数进行惩罚,降低特征参数的影响,通常如下:
损失函数–Loss Function– Softmax(Multinomial Logistic Regression)
- 函数公式很简单,参照以下公式:

EXP和normalize的作用将score归一化到[0,1]之间。
- 计算方式:

损失函数总结
- Softmax对于scores值变化较为敏感,而SVM对于Scores值微小变化不敏感,意味着SVM具有较大鲁棒性,Softmax具有较强灵敏性。
- 通过数据集和标签(x,y)——>乘以特征参数W和偏置b,计算scores——>通过损失函数计算Loss
- 如何优化参数,最佳的W—->Optimization
最优化-Optimization
- 最优化问题就像在一个山谷中寻找最低点
- 不理智的策略:采用随机的方式去寻找最佳W矩阵,能够寻找到合适的点,但是准确率不高
- 跟随斜率/梯度
- 数值计算斜率的方法如下:
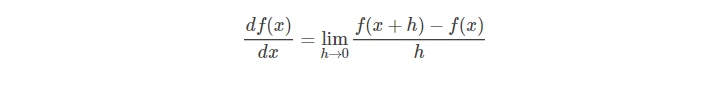
- 多维的情况下,梯度等同于偏导数,独立对每一维度进行计算
- 但是对于一个损失函数和W,步长是不确定,同时对于上面的损失函数,是一个W的函数
- 对于求梯度,可以转换为使用微积分(calculus)求取解析解,(反向传播),再使用学习率进行更新
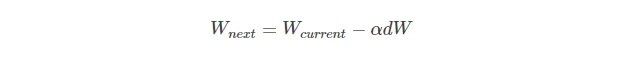
- 数值法优缺点:估算;速度慢;易于coding
- 解析法优缺点:准确;速度快;易出错(特别是在某些函数不可导点)
- 梯度检验:
- 如何证明更新后的参数是正确的,可以使用数值解的逼近计算方式来验证求取的梯度是否正确
- 数值计算斜率的方法如下:
- 梯度下降法–随机梯度下降法(SGD-stochastic)
- 当数据集比较大的时候,计算代价非常大(占用内存);计算会非常慢(图像越多,需要优化的参数成倍增长)
- 使用mini-batch进行训练,通常一组为32/64/128,大小与内存大小成比例,使用这种方法损失函数会在波动中下降。
- 学习率不同优化速度不同:太高跨度大无法收敛;太小收敛速度慢;较高无法收敛到最佳点,会找到局部最优;合适的值才能有快又好。
- 其他的梯度下降法还有:Momentum(冲量法)、NAG(牛顿法)、Adagrad、Adadelta、RMSprop等
图像特征提取
- 特征提取
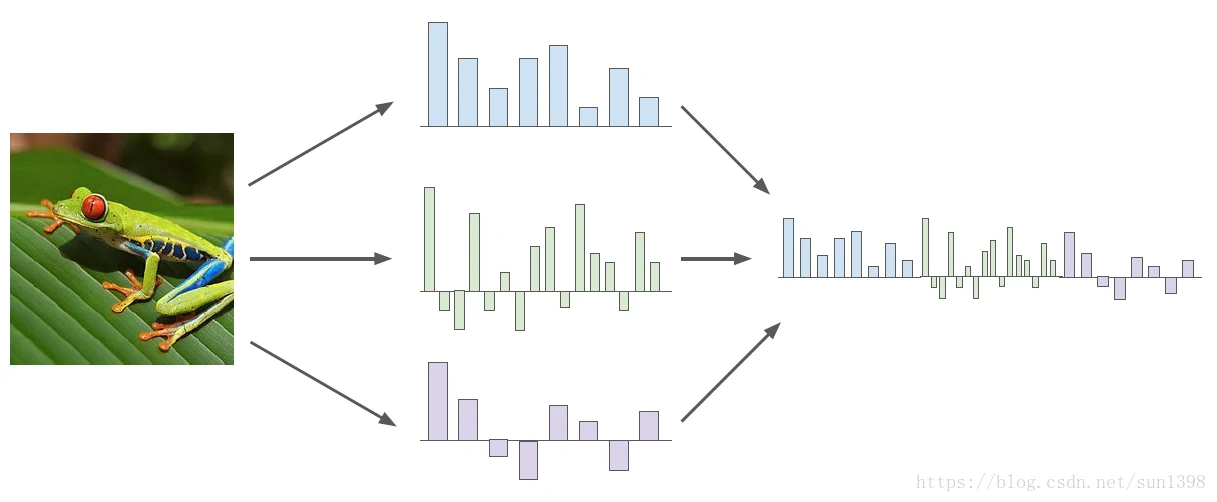
- 特征提取作为某些统计特征来进行分类
- 推动力

- 特征提取的推动力在于将以前不能区分的类别,通过函数映射变化成为直观可区分的类
实例
- Color Histogram:通过提取不同颜色通道的值作为特征
- Histogram of Oriented Gradients (HoG):通过提取图像的不同旋转方向的梯度统计直方图来作为特征
- Bag of Words:通过提取某些分类的特征作为编码,比如猫的耳朵、青蛙的脚;再通过这些特征作为解码去恢复图片
特征提取VS神经网络
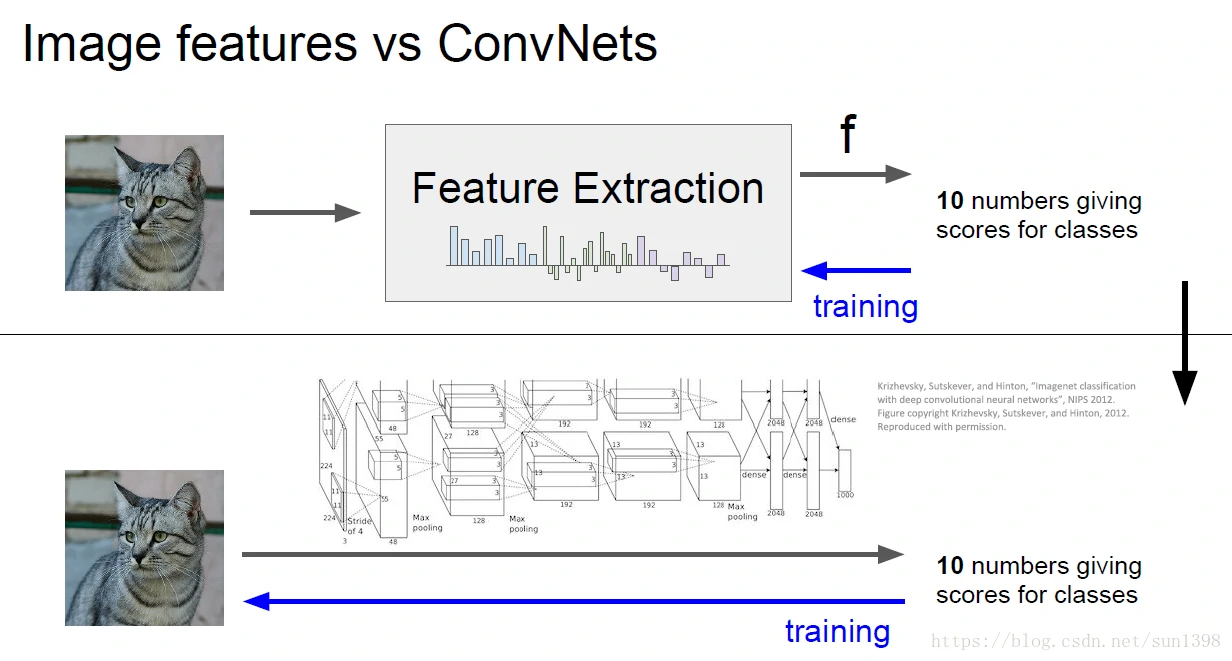
2012年前图片分类广泛采用特征提取+线性分类(特别是SVM),在特定领域方向具有价值,具有专用性,但缺乏通用性与广泛性。
2012年后imagenet的Alexnet网络已极高的准确率打败传统方法后,随着算力和数据爆炸式增长而崛起。