深度学习-归一化层BN、LN、IN、GN、SN

综述

归一化层，目前主要有这几个方法，Batch Normalization（2015年）、Layer Normalization（2016年）、Instance Normalization（2017年）、Group Normalization（2018年）、Switchable Normalization（2018年）

将输入的图像 shape 记为 [N, C, H, W]，这几个方法主要的区别就是在：

BatchNorm是在 batch 上，对 NHW 做归一化，就是对每个单一通道输入进行归一化，这样做对小 batchsize 效果不好
LayerNorm在通道方向上，对 CHW 归一化，就是对每个深度上的输入进行归一化，主要对 RNN 作用明显
InstanceNorm在图像像素上，对 HW 做归一化，对一个图像的长宽即对一个像素进行归一化，用在风格化迁移
GroupNorm将 channel 分组，有点类似于 LN，只是 GN 把 channel 也进行了划分，细化，然后再做归一化
SwitchableNorm是将 BN、LN、IN 结合，赋予权重，让网络自己去学习归一化层应该使用什么方法

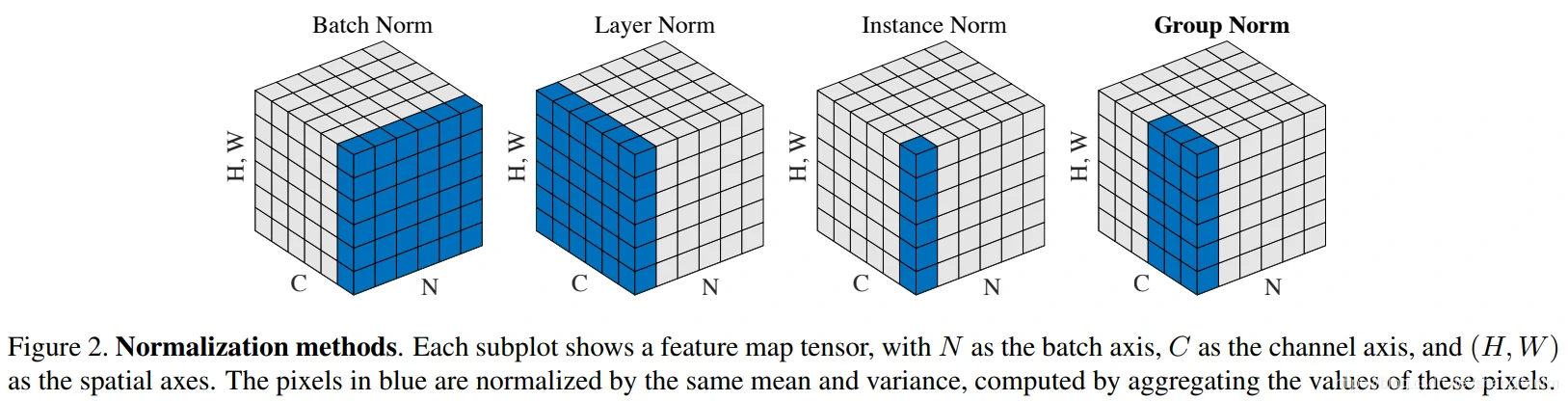
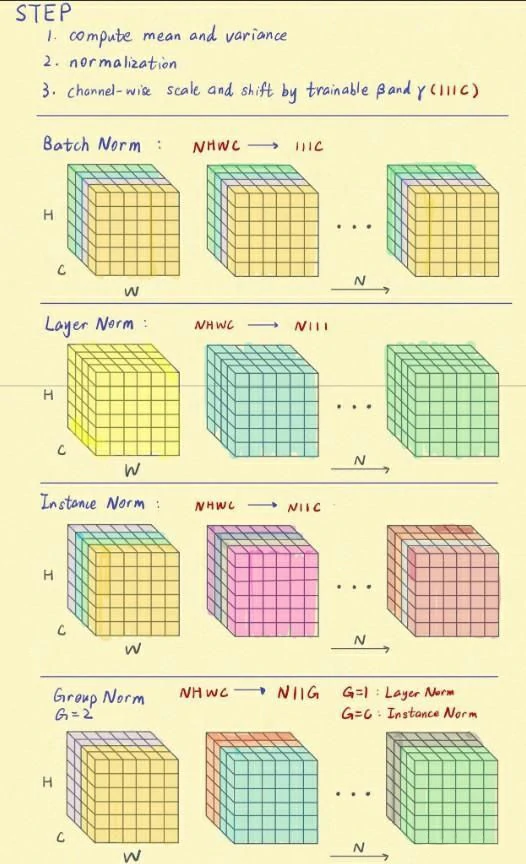
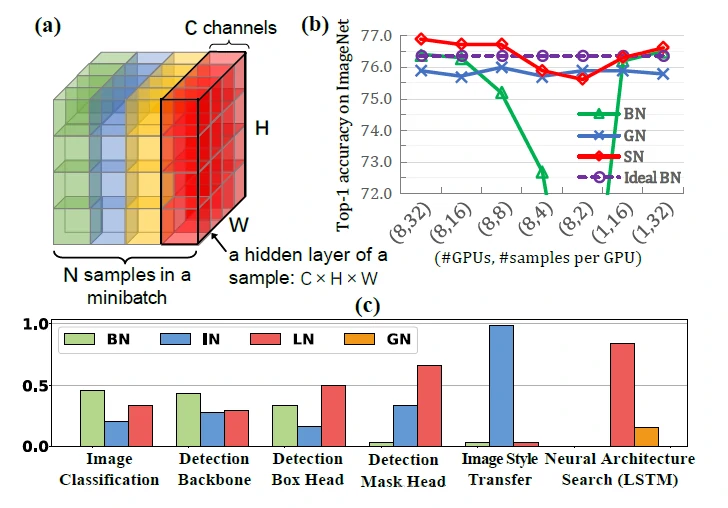
图中每一个正方体块表示一个数据（比如说这里一个正方体就是一个图像）
每一个正方体中的C, H, W分别表示channel(通道个数), height(图像的高), weight(图像的宽)
Norm 的方式，如Layer Norm中NHWC->N111表示是将后面的三个进行标准化，不与 batch 有关
我们可以看到，后面的LayerNorm, InstanceNorm和GroupNorm这三种方式都是和 batch 是没有关系的

Batch Normalization

论文：Batch Normalization

首先，在进行训练之前，一般要对数据做归一化，使其分布一致，但是在深度神经网络训练过程中，通常以送入网络的每一个 batch 训练，这样每个 batch 具有不同的分布；此外，为了解决 internal covarivate shift 问题，这个问题定义是随着 batch normalizaiton 这篇论文提出的，在训练过程中，数据分布会发生变化，对下一层网络的学习带来困难。

所以 batch normalization 就是强行将数据拉回到均值为 0，方差为 1 的正态分布上，这样不仅数据分布一致，而且避免发生梯度消失。

此外，internal corvariate shift和covariate shift是两回事，前者是网络内部，后者是针对输入数据，比如我们在训练数据前做归一化等预处理操作。

算法过程：

沿着通道计算每个 batch 的均值 u
沿着通道计算每个 batch 的方差 σ^2
对 x 做归一化，x’ = (x - u) / √(σ^2 + ε)
加入缩放和平移变量 γ 和 β ，归一化后的值，y = γx’ + β

加入缩放平移变量的原因是：保证每一次数据经过归一化后还保留原有学习来的特征，同时又能完成归一化操作，加速训练。这两个参数是用来学习的参数。

import numpy as np

def Batchnorm(x, gamma, beta, bn_param):

    # x_shape:[B, C, H, W]
    running_mean = bn_param['running_mean']
    running_var = bn_param['running_var']
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(0, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(0, 2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta

    # 因为在测试时是单个图片测试，这里保留训练时的均值和方差，用在后面测试时用
    running_mean = momentum * running_mean + (1 - momentum) * x_mean
    running_var = momentum * running_var + (1 - momentum) * x_var

    bn_param['running_mean'] = running_mean
    bn_param['running_var'] = running_var

    return results, bn_param

Layer Normalizaiton

论文：Layer Normalizaiton

Batch Normalization 存在以下缺点：

对 batchsize 的大小比较敏感，由于每次计算均值和方差是在一个 batch 上，所以如果 batchsize 太小，则计算的均值、方差不足以代表整个数据分布
BN 实际使用时需要计算并且保存某一层神经网络 batch 的均值和方差等统计信息，对于对一个固定深度的前向神经网络（DNN，CNN）使用 BN，很方便；但对于 RNN 来说，sequence 的长度是不一致的，换句话说 RNN 的深度不是固定的，不同的 time-step 需要保存不同的 statics 特征，可能存在一个特殊 sequence 比其他 sequence 长很多，这样 training 时，计算很麻烦。

与 BN 不同，LN 是针对深度网络的某一层的所有神经元的输入按以下公式进行 normalize 操作。

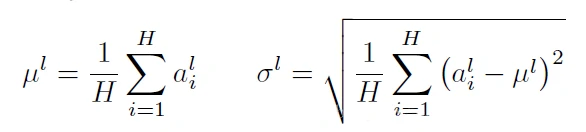
BN与LN的区别在于：

LN 中同层神经元输入拥有相同的均值和方差，不同的输入样本有不同的均值和方差；
BN 中则针对不同神经元输入计算均值和方差，同一个 batch 中的输入拥有相同的均值和方差。

所以，LN 不依赖于 batch 的大小和输入 sequence 的深度，因此可以用于 batchsize 为 1 和 RNN 中对边长的输入 sequence 的 normalize 操作。

LN 用于 RNN 效果比较明显，但是在 CNN 上，不如 BN。

def ln(x, b, s):
    _eps = 1e-5
    output = (x - x.mean(1)[:,None]) / tensor.sqrt((x.var(1)[:,None] + _eps))
    output = s[None, :] * output + b[None,:]
    return output

用在四维图像上：

def Layernorm(x, gamma, beta):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(1, 2, 3), keepdims=True)
    x_var = np.var(x, axis=(1, 2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

Instance Normalization

论文：Instance Normalization
论文实现：https://github.com/DmitryUlyanov/texture_nets

BN 注重对每个 batch 进行归一化，保证数据分布一致，因为判别模型中结果取决于数据整体分布。

但是图像风格化中，生成结果主要依赖于某个图像实例，所以对整个 batch 归一化不适合图像风格化中，因而对 HW 做归一化可以加速模型收敛，并且保持每个图像实例之间的独立。

def Instancenorm(x, gamma, beta):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    x_mean = np.mean(x, axis=(2, 3), keepdims=True)
    x_var = np.var(x, axis=(2, 3), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

Group Normalization

论文：Group Normalization

主要是针对 Batch Normalization 对小 batchsize 效果差，GN 将 channel 方向分 group，然后每个 group 内做归一化，算 (C // G) * H * W 的均值，这样与 batchsize 无关，不受其约束。

def GroupNorm(x, gamma, beta, G=16):

    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5
    x = np.reshape(x, (x.shape[0], G, x.shape[1]/16, x.shape[2], x.shape[3]))

    x_mean = np.mean(x, axis=(2, 3, 4), keepdims=True)
    x_var = np.var(x, axis=(2, 3, 4), keepdims=True0)
    x_normalized = (x - x_mean) / np.sqrt(x_var + eps)
    results = gamma * x_normalized + beta
    return results

Switchable Normalization

论文：Switchable Normalization
论文实现：https://github.com/switchablenorms/Switchable-Normalization

本篇论文作者认为：

归一化虽然提高模型泛化能力，然而归一化层的操作是人工设计的。在实际应用中，解决不同的问题原则上需要设计不同的归一化操作，并没有一个通用的归一化方法能够解决所有应用问题；
一个深度神经网络往往包含几十个归一化层，通常这些归一化层都使用同样的归一化操作，因为手工为每一个归一化层设计操作需要进行大量的实验。

因此作者提出自适配归一化方法 Switchable Normalization（SN）来解决上述问题。与强化学习不同，SN 使用可微分学习，为一个深度网络中的每一个归一化层确定合适的归一化操作。

def SwitchableNorm(x, gamma, beta, w_mean, w_var):
    # x_shape:[B, C, H, W]
    results = 0.
    eps = 1e-5

    mean_in = np.mean(x, axis=(2, 3), keepdims=True)
    var_in = np.var(x, axis=(2, 3), keepdims=True)

    mean_ln = np.mean(x, axis=(1, 2, 3), keepdims=True)
    var_ln = np.var(x, axis=(1, 2, 3), keepdims=True)

    mean_bn = np.mean(x, axis=(0, 2, 3), keepdims=True)
    var_bn = np.var(x, axis=(0, 2, 3), keepdims=True)

    mean = w_mean[0] * mean_in + w_mean[1] * mean_ln + w_mean[2] * mean_bn
    var = w_var[0] * var_in + w_var[1] * var_ln + w_var[2] * var_bn

    x_normalized = (x - mean) / np.sqrt(var + eps)
    results = gamma * x_normalized + beta
    return results

在Pytorch上的实现

BatchNorm

1
2
3

torch.nn.BatchNorm1d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
torch.nn.BatchNorm3d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)

参数	解释
num_features	来自期望输入的特征数，该期望输入的大小为 batch_size x num_features [x width]
eps	为保证数值稳定性（分母不能趋近或取0），给分母加上的值。默认为1e-5。
momentum	动态均值和动态方差所使用的动量。默认为0.1。
affine	布尔值，当设为true，给该层添加可学习的仿射变换参数。
track_running_stats	布尔值，当设为true，记录训练过程中的均值和方差。

实现公式：

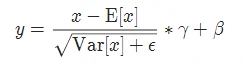
LayerNorm

1	torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True)

参数	解释
normalized_shape	输入尺寸 [∗×normalized_shape[0] × normalized_shape[1] × … × normalized_shape[−1]]
eps	为保证数值稳定性（分母不能趋近或取0），给分母加上的值。默认为1e-5。
elementwise_affine	布尔值，当设为true，给该层添加可学习的仿射变换参数。

实现公式：

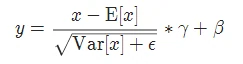
InstanceNorm

1
2
3

torch.nn.InstanceNorm1d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)
torch.nn.InstanceNorm3d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False)

参数	解释
num_features	来自期望输入的特征数，该期望输入的大小为 batch_size x num_features [x width]
eps	为保证数值稳定性（分母不能趋近或取0），给分母加上的值。默认为1e-5。
momentum	动态均值和动态方差所使用的动量。默认为0.1。
affine	布尔值，当设为true，给该层添加可学习的仿射变换参数。
track_running_stats	布尔值，当设为true，记录训练过程中的均值和方差。

实现公式：

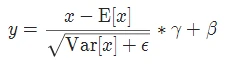
GroupNorm

1	torch.nn.GroupNorm(num_groups, num_channels, eps=1e-05, affine=True)

参数	解释
num_groups	需要划分为的groups
num_features	来自期望输入的特征数，该期望输入的大小为 batch_size x num_features [x width]
eps	为保证数值稳定性（分母不能趋近或取0），给分母加上的值。默认为1e-5。
momentum	动态均值和动态方差所使用的动量。默认为0.1。
affine	布尔值，当设为true，给该层添加可学习的仿射变换参数。

实现公式：

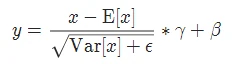
总结

类似情况

当 GroupNorm 中group的数量是 1 的时候，是与 LayerNorm 是等价的
InstanceNorm 等价于当 GroupNorm 时 num_groups 的数量等于 num_channel 的数量

每一种方式适合的场景

BatchNorm 是在 batch 上，对小 batchsize 效果不好
LayerNorm 在通道方向上，主要对 RNN 作用明显
InstanceNorm 在图像像素上，用在风格化迁移
GroupNorm 将 channel 分组，然后再做归一化, 在 batchsize < 16 的时候, 可以使用这种归一化

参考资料

https://blog.csdn.net/shanglianlm/article/details/85075706
https://zhuanlan.zhihu.com/p/395855181
https://blog.csdn.net/liuxiao214/article/details/81037416