什么是KKT
KKT条件(Karush Kuhn Tucker conditions)是最优化(特别是非线性规划)领域最重要的成果之一,是判断某点是极值点的必要条件。
可理解好它需要用到梯度、松弛变量、对偶理论等知识,想讲好KKT条件是具有一定难度的。
本文第一部分侧重于理论部分,第二部分给出运用KKT条件进行数值和符号运算的Matlab代码。基于此,大家可以非常方便地应用于自己的论文写作。
在介绍KKT条件之前,先补充些基础知识。
何谓最优化问题
要选择一组参数(变量),在满足一定的限制条件(约束)下,使设计指标(目标)达到最优值。
根据定义,古诺模型和Stackelberg模型是最优化问题,只不过它们均没有约束,直接对决策变量求导便能得到最优值。
进一步,根据有无约束以及约束特征,可以将最优化问题分为以下三类,每类问题的求解方法也紧跟着列出。
最优化问题分类
无约束优化问题:直接求导、最速下降法、共轭梯度法、牛顿法等;
等式约束优化问题:拉格朗日(Lagrange)乘数法;
不等式约束优化问题:KKT条件。
大家做科研时也要分清楚自己的问题属于哪一类,然后运用对应的求解方法。
以上知识点在本科的《运筹学》和《高等数学》课程中均学过。前两类相对简单,至于KKT条件,大家会被课本上复杂的数学公式劝退,即使考前重温,过段时间又会忘。
所以,本文不先从那些复杂公式入手,而是以我的理解,带大家一起探索下Karush–Kuhn–Tucker这三个人,是如何发现并总结出KKT条件的。
KKT条件理论部分
该部分先介绍KKT条件的核心思想,即λg(X*)=0公式的由来;再解释为什么课本上的数学公式长那样,最后再针对性地给出一些补充说明和数学证明。
KKT条件核心思想
时光倒流,假设你是还没提出KKT条件的Karush本人,面对不等式约束优化问题,会如何思考呢?
先观察下仅含有一个不等式约束的优化问题:

注:如果是最大化问题,即maxf(X),约束改写为g(X*)≥0的形式(原因后文会解释)。
既然默认还不知道KKT条件,所以目前咱们还不会解决该问题。但不急,想想咱们会啥?会求求导数,同时也会等式约束下的拉格朗日乘数法啊。
一步步来,先对f(X)函数求导吧(若X多维则是求梯度),即先不考虑g(X)≤0这个约束。
毕竟求导或求梯度,Karush和你都是会的。此时会得到“使f(X)取最小值时的最优X”,进一步,如果将其值X*带入约束g(X),无非就以下三种情况。
(1)g(X*)<0
那正好满足约束,X就是我们要找的最优解。
猛然发现,此时该约束完全不起作用啊(称为不起作用约束),毕竟我们计算X*时压根都没考虑它。
(2)g(X*)=0
也就是最优解X*正好也让约束取了等号。
这咱们也熟啊,这不转化为含有等式约束的优化问题了嘛。如何求解?拉格朗日乘数法啊,安排~
(3)g(X*)>0
显然此时的X*不满足约束,应舍弃。
但这并没有结束,我们需要给出一个解,那此时大家觉得X*会在哪?很简单,无非又变回了情形(1)或(2)。
综上,我们只需要分情况讨论清楚若g(X)<0和若g(X)=0时,应该如何求解即可**。
一通分析下来,大家或许此时感觉自己好像已经会了,不就是:
若g(X*)<0,约束不起作用,该问题转化为无约束优化问题求解;
若g(X*)=0,引入拉格朗日乘子λ,采用拉格朗日乘数法求解嘛,其间,构造的拉格朗日函数如下(这是拉格朗日乘数法的知识,不了解的同学可以自行简单重温下)。
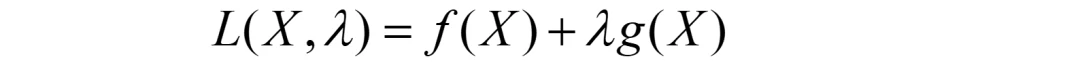
理确实这么个理,但人家数学家追求的是能否有个统一的形式来求解?这样分类讨论可不那么高大上啊。
既然都已经引进拉格朗日乘子λ了,那也得想办法使得在g(X*)<0情形下,也要与λ有点关系。
考虑到若g(X*)<0,此时该约束不起作用,而已经构造好的拉格朗日函数中又有λ,怎么办?
很简单,让拉格朗日函数中的λ=0即可!此时拉格朗日函数可不就简化为L(x, λ)=f(X)了嘛。此时对L(x, λ)求导(等价于对f(X)求导)时既不用管约束,也没有λ的干扰,简直完美。
汇总一下就是:
(1)若g(X*)=0,引入拉格朗日乘子λ,并要求λ≥0;
(2)若g(X*)<0,要求λ=0。
那怎么统一呢?数学家灵魂附体!脑袋一拍,含泪发现,这不就可以采用λg(X*)=0的形式统一了嘛。
恭喜你,你代替Karush本人提出了λg(X*)=0!而这,就是KKT条件的精髓。
是不是有点难以置信,但确实,KKT条件的核心思想和公式其实已经讲完了。
不复杂吧,基础思想确实是很简单的,毕竟早在1939年,Karush在其硕士学位论文里就已经给出了KKT条件。硕士生啊,哎,差距。
KKT条件的数学公式
掌握了思想,便可以更好地看懂课本上的公式了。
还是由简到难,先给出仅含有一个不等式约束的KKT条件。

这里还需要借助上一部分给出的拉格朗日函数来理解。
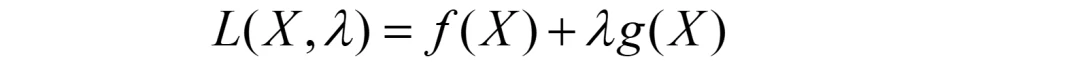
简单分析**公式(1)-(4)**可知:
式(1):对拉格朗日函数求梯度(若X一维就是求导),其中,下三角表示梯度;
式(2):核心公式,要么λ=0,要么g(X*)=0(此处要求两者不能同时为0);
式(3):拉格朗日乘子λ必须是正的(下一部分的图示法有证明);
式(4):原问题自己的约束。
可见,式(1)和(2)都是等式,可以帮助我们求最优X*和λ,因为式(2)要分类讨论,所以可能存在多个X*和λ;式(3)和(4)主要起验证作用,帮助我们排除掉一些不满足式(3)和(4)的X*和λ。
具体地,在应用KKT条件计算时,通常也是分类讨论后先求解X*和λ,再验证其是否满足式(3)和(4),从而排除一些解。
像上述仅含有一个约束的例子,只需要分两类,通常是以拉格朗日乘子λ是否为0进行分类:
(1) 当 λ=0 时,计算X*的值,并验证g(X*)≤0是否成立;
(2) 当 λ≠0 时,计算X*和λ的值,并验证g(X*)≤0和λ≥0是否成立。
下面,将KKT条件推广至含有多个等式约束和不等式约束的情况。也是课本上给初次学习KKT条件的同学提供的公式,劝退了好多人。
考虑的最优化问题为:
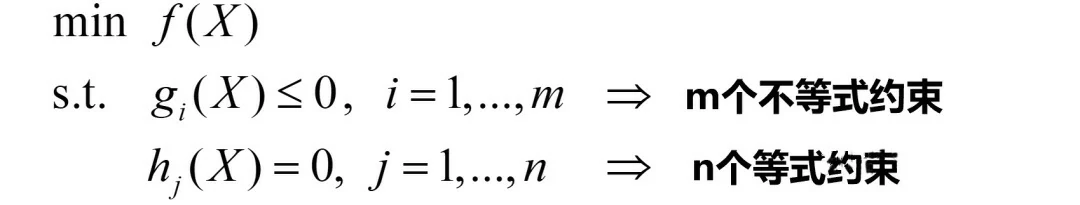
此时定义的拉格朗日函数为:
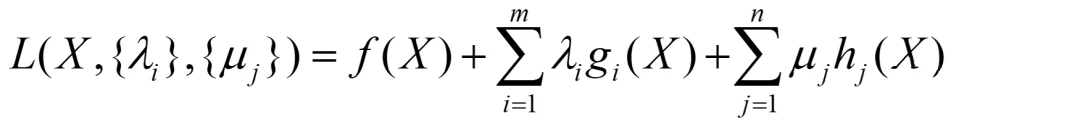
其中,**{λi}指的是一系列的λ(有m个),同理{μj}**也是。由于是多个约束,因此引入求和号∑。
其对应的KKT条件为:
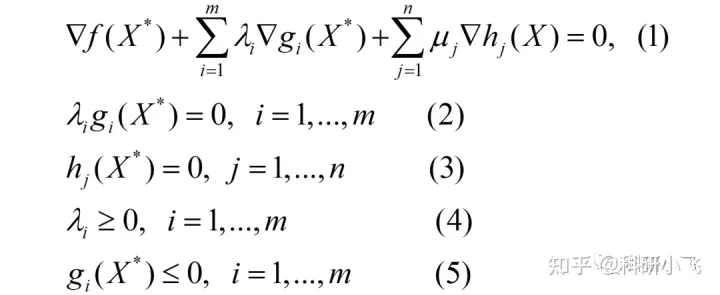
不要被上述形式吓到了,解题思路与之前叙述类似,就是用几个等式计算最优值,用不等式验证这些值,不满足则排除。
即,利用式(1)(2)(3)求最优X*和λi,然后通过式(4)和(5)验证这些解是否可行,“可行”指的是这些解是否能让(4)和(5)的不等号成立,不成立则排除。注意,μj是可以取任意值的,不受限制。因为它们是等式约束的拉格朗日乘子,不是不等式的乘子。
由于该问题有m个不等式约束,每个约束对应的拉格朗日/KKT乘子λi都可以“=0”或“≠0”。因此,需要分类讨论的情况有2^m种。
分类详情如下:(1) 当λ1=0,λ2≠0,……,λm≠0时;(2) 当λ1=0,λ2=0,……,λm≠0时;……在此,不再展开,本文第四部分会给出算例来做具体说明。
至此,从特殊到一般的KKT条件讲解完毕,总结一下,当我们应用KKT条件求解算例时,可以采用如下思路:
能解出最优解的一定是等式,故式(1)(2)(3)帮我们求最优解;
式(4)和式(5)是不等式,帮我们排除一些解,或者得到最优解的适用范围。
这里有必要解释下“得到最优解的适用范围”这句话。其主要针对符号运算的情形,看完第四部分的算例,会有更深的理解,这里仅作为引子简单提一下:
大家在写论文时,建立的数学模型多是用参数和变量表示的,不同情形下的最优解也是符号表达式,因此很难比较大小。
此时,只能通过式(4)和(5),来得到在什么条件(某符号表达式满足某条件)下,最优解X*和对应的f(X*)值为多少,即需要分类讨论。
具体如何应用上述理论求解具体的算例,并撰写Matlab代码,放在第四部分讲解,本部分着重讲解理论。
KKT条件补充说明
该部分主要强调KKT条件的适用范围和部分理论的数学证明。
充分性、必要性说明
首先强调的是,KKT条件是判断某点是极值点的必要条件,不是充分条件。换句话说,最优解一定满足KKT条件,但KKT条件的解不一定是最优解。
对于凸规划,KKT条件就是充要条件了,只要满足KKT条件,则一定是极值点,且得到的一定还是全局最优解。
凸规划指的是:目标函数为凸函数,不等式约束函数也为凸函数,等式约束函数是仿射的(理解成是线性的也行)。这牵扯到另一个领域了,本文不再展开陈述。
补充:我知道很多同学会问,目标函数是凹函数就不能解了?并不是的,凸规划/凸优化只研究凸函数的最小化问题,并且认为凹函数的最大化问题是与它等价的。毕竟凹函数只需加个负号就是凸函数了,所以在研究问题中,就不再提凹函数了。
Min/Max与“≤0”和“≥0”的规定
这里指的是(该部分也是本文的重点部分,划重点):
(1)如果目标为最小化(Min)问题,那么不等式约束需要整理成“≤0”的形式;
(2)如果目标为最大化(Max)问题,那么不等式约束需要整理成“≥0”的形式;
以仅含有一个不等式约束的情形为例,最小化和最大化的优化问题要整理成如下形式:
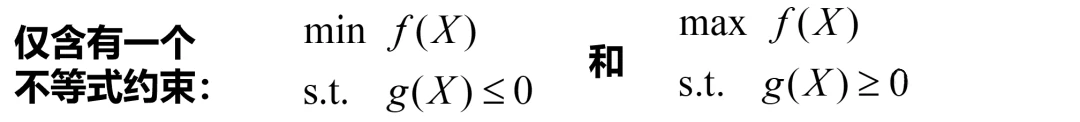
该形式可以死记硬背,但时间一长,大家可能会忘记或记混了,下面,采用图示法逐步展示为什么会有这个要求,该分析过程也展现了KTT条件的几何思想。
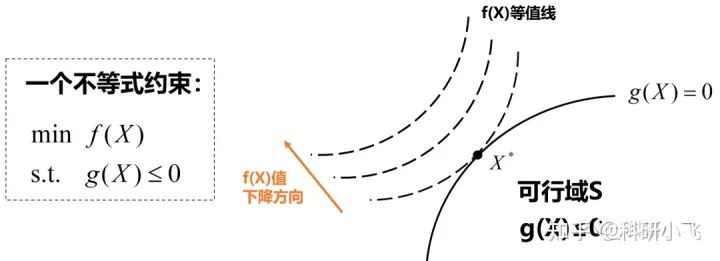
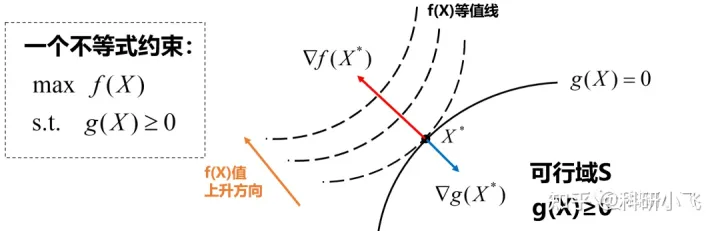
上图画出了3条f(X)函数的等值线(图中虚线),以及右下角为可行域S(即约束条件规定的区域)和g(X)=0的曲线,最优解为**X***。基于此,具体分析如下:
(1)f(X)函数值下降方向为左上方:
目标是最小化问题,若下降方向为右下方,则最优解(图中X*)一定不是在g(X)=0上,而是在可行域S内部
由于KKT条件中第一条就需要计算f(X)和g(X)函数的梯度,所以,这里补充一个基础知识:梯度方向垂直于函数等值线,指向函数值增长的方向。
基于此,我们尝试画出f(X)和g(X)函数的梯度方向:
(2)画出f(X)的梯度方向(下图红色方向):
梯度方向是函数值增长的方向,因此指向右下方;负梯度方向是函数值下降的方向,指向左上方;
(3)画出g(X)的梯度方向(下图蓝色方向):
由于曲线是g(X)=0,右下方是g(X)<0,是在下降,因此,g(X)函数值增长的方向就是左上方了。
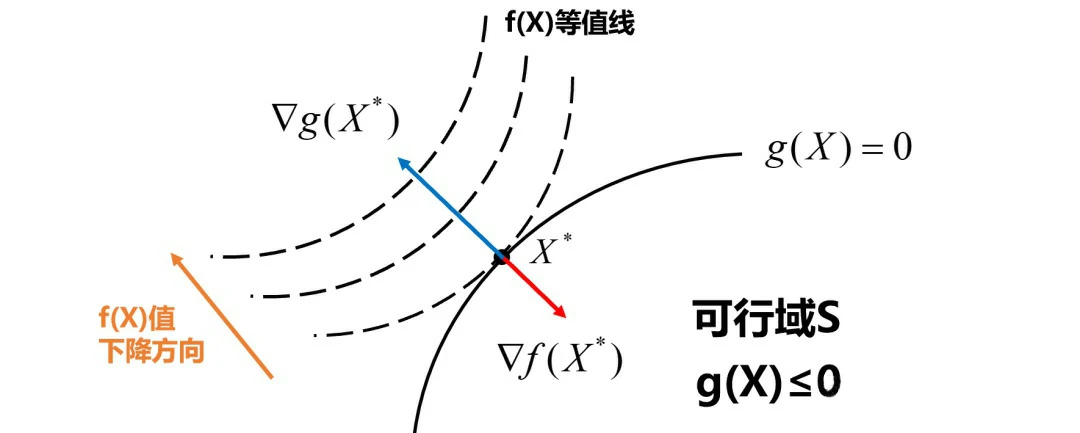
由上述分析和上图可知,在最优解X*处,f(X*)和g(X*)的梯度方向共线且方向相反。向量共线且方向相反在数学上的写法就是:
负梯度向量是另一个梯度向量的λ倍。移项后发现,这不就是KKT条件的第一个等式嘛!
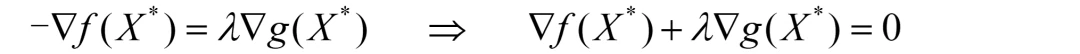
同时可知,λ的值只能取正值,因为g(X)的梯度方向与f(X)负梯度方向相同。这也是KKT条件要求 λ≥0 的原因。
基于以上分析可知:最小化问题的约束条件应该整理成“≤0”的形式,且λ≥0。
同理,最大化的分析不再展开,仅给出分析图,有兴趣的同学可以自己动手分析一下。
补充一点,对于最大化问题,如果可行域也非要写成g(X)≤0的形式,能行吗?先别忙着否定,我们分析一下。
此时g(X*)的梯度方向就不再是右下方了(不是上图了),而是f(X*)与g(X*)的梯度方向相同,有:
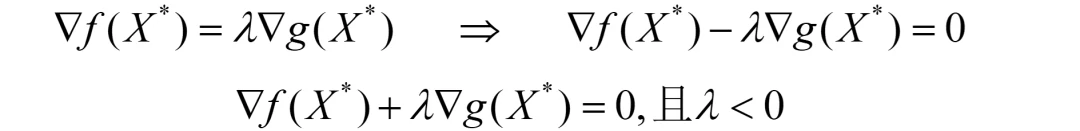
此时如上图,要么KKT条件第一项改为“作差”,要么让λ<0。无论哪一个,其实都是徒增烦恼。不如上来就规定约束写成g(X)≥0来的方便。
因此,最大化问题的约束条件应该整理成“≥0”的形式,且λ≥0。
下面推广到多约束条件的情形,仅是把梯度的共线变为梯度的线性组合,若不好理解,可跳过。
假设有起作用约束g1(X)和起作用约束g2(X)共同影响目标函数f(X)的梯度,又是怎么样的图形呢?
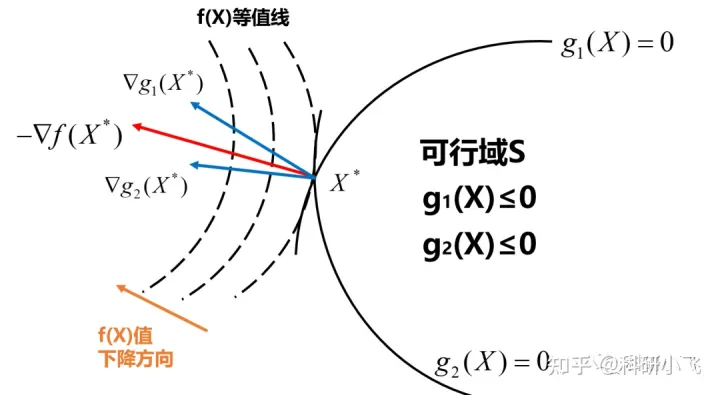
我们分别画出g1(X)函数在X*处的梯度,如图中蓝色向量,其垂直于曲线g1(X*)=0;同理,画出g2(X)函数在X*处的梯度,是另一个蓝色向量。
至于f(X)函数的梯度,图中画出负梯度方向(函数值下降的方向),这样画的好处是可以直观地看出三个梯度向量间的关系:
f函数的负梯度可以表示成g1函数和g2函数梯度的线性组合。则有如下公式:
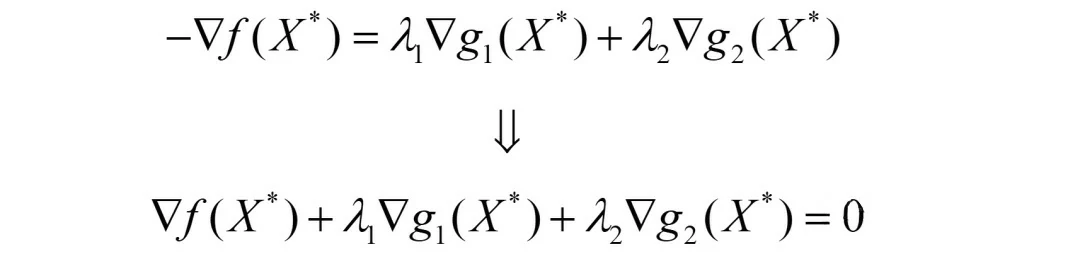
简单移项后,又发现了我们的老朋友:KKT条件的第一个等式。从图中也可以看出,梯度向量之间的夹角为锐角,因此也有λ1≥0,λ2≥0的要求。
看完这部分内容,相信大家对于课本上关于KKT条件的的数学公式和图形,能记忆也能自己推导了。
正则性条件/约束规范说明
KKT条件对于目标函数和约束函数也是有要求的。该部分数学性较强,不好理解可跳过。
目标函数和约束函数(f、g1、… 、gm、h1、… 、hn函数)均为连续可微函数。
上述是我们熟知的要求,事实上,并不完全正确(严谨),还缺少一个regularity条件(也被成为正则性条件或者约束规范(constraint qualification))。
其含义指:以下方程组是线性独立的。
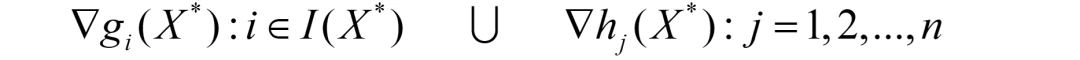
其中,I(X*)指的是起作用约束的集合。
这里不再深入展开,具体算例可参见B站视频《KKT条件为什么用不了了》:
几类非光滑函数的转化
上一节指出,运用KKT条件时,要求函数连续可微。可有些函数很常见,但却存在不可微的点,此时就可以想办法转化下。
(1)目标函数:f(x) = max(x, x^2)
即目标函数f(x)存在不可微点:简单画图可知,该函数在 (0, 0) 点和 (1, 1) 点处不可微。此时可以引入变量y,进行如下转化。
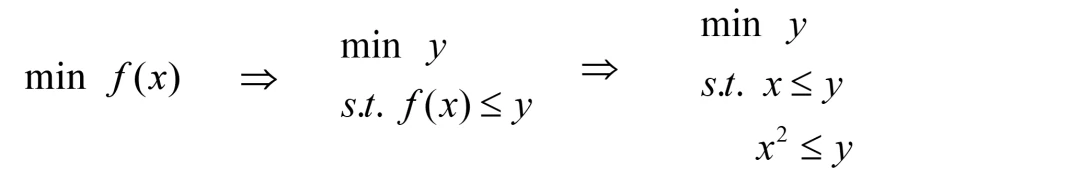
强调一下,虽然这个看着简单,但其实应用挺广,比如对如下k个线性函数求最大。
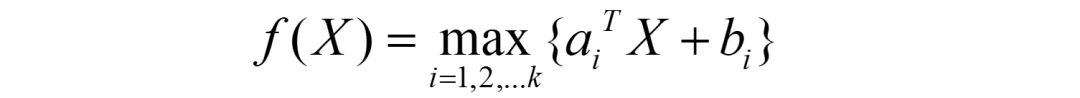
(2)约束条件:g(x) = |x1| + |x2| ≤ 1
即约束条件g(x)存在不可微点:我们知道,绝对值函数的含义为 |x| = max(x, -x)。而g(x)中有两个绝对值,故可以如下转化。
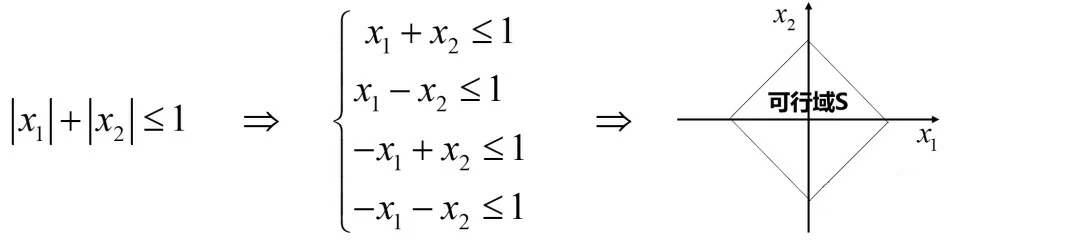
可见,g(x)函数转化成了四个约束,四个约束都是线性,就可以用KKT条件了。当然,对于这种简单的形式,画图求解也许会更方便。
总的来说,绝对值函数的线性化较为简单,而更多的线性化方法/技巧,可以参见常见的线性化方法/技巧(上)和常见的线性化方法/技巧(下)或者令人拍案叫绝的线性化方法/技巧。
KKT条件与KT条件
1951年,Kuhn和Tucker发现了KKT条件并撰写了论文将其正式发表出来,当然,此时他们不知道另一个K是谁,故命名为Kuhn-Tucker(库恩塔克)条件,也就是KT条件。
很快,他们的成果引起了很多很多学者的重视。树大招风,其中一些学者发现早在1939年,Karush在其硕士学位论文里边已经给出了KKT条件,只是当时没有引起广泛关注而已。
不过,后来大家都承认Kuhn,Tucker,Karush三位都是独立发现KKT条件的学者。故此后命名多加了个K。
数值与符号运算(重点)
简单回顾下KKT条件:
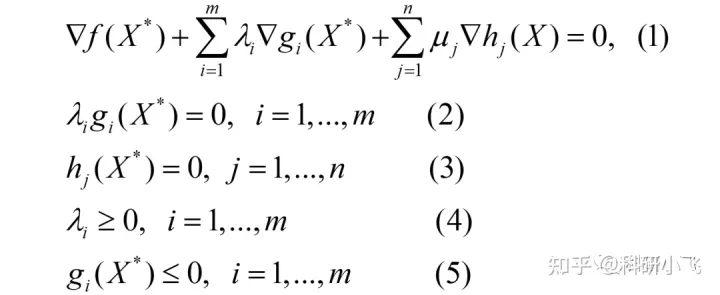
还记得解题思路吗?
能解出最优解的一定是等式,故式(1-3)帮我们求最优解;
式(4-5)是不等式,帮我们排除一些解,或者得到最优解的适用范围。
这也是口诀“等式求最优,不等式验证”的由来。
下面,我们来看下数值/符号运算中,KKT条件是如何求解最优化问题的。数值计算例子为求解最小化问题,符号运算例子为求解最大化问题。
先看下课本上的例题,是如何应用KKT条件进行数值计算的。
数值计算实操
我们想用KKT条件求解如下非线性最优化问题:
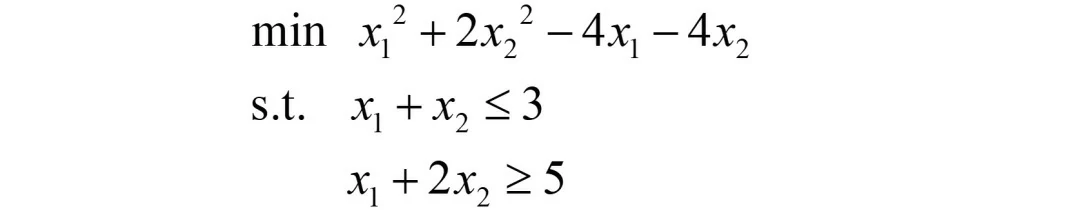
观察约束,发现有“≥0”的形式,由本文第二三部分可知,需要统一转化为“≤0”的形式,故上述问题的标准形式为:
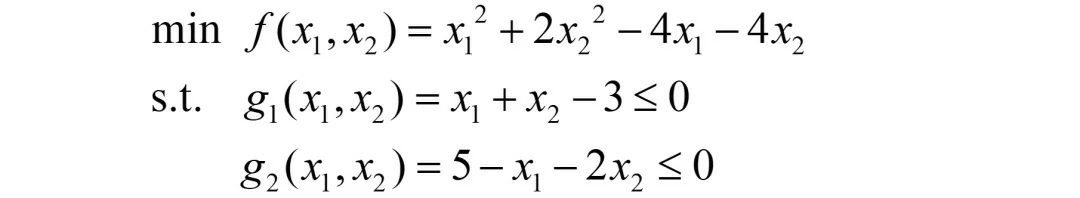
基于该标准形式,构造的拉格朗日函数为:
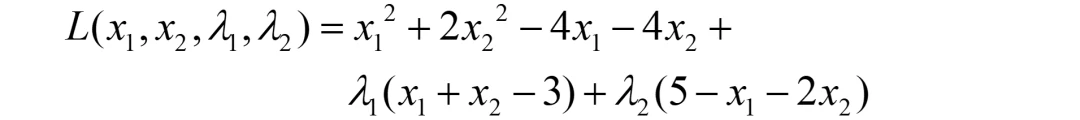
对其中的x1和x2分别求导,得到如下两等式:
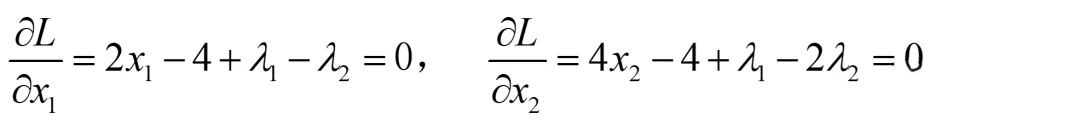
有些同学习惯用梯度表示,也可以,两种方法一致,看大家熟悉哪种了:
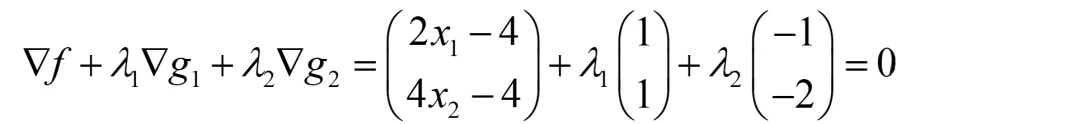
数一下,有四个未知数,但求导后只有两个等式方程,显然还无法求解,此时KKT条件的核心公式**λigi=0(i=1,2)**就派上用场了。
λigi=0(两者不同时为0)+ KKT条件中的不等式,具体含义为:
(1)若λ1=λ2=0,则g1<0,g2<0;
(2)若λ1=0,λ2>0,则g1<0,g2=0;
(3)若λ1>0,λ2=0,则g1=0,g2<0;
(4)若λ1>0,λ2>0,则g1=0,g2=0;
仔细观察上述每一种情形,均包含了两个等式方程,加上之前求导得到的两个方程,总共四个方程,这回就可以求解四个未知数了。
那还等啥,直接求解吧。
(i)若λ1=λ2=0,则g1<0, g2<0
无论哪种情形,主要是求解上面写的求导后的/梯度方程,即:
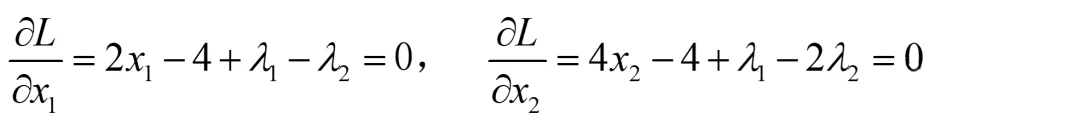
若λ1=λ2=0,则只需要求解x1,x2即可:
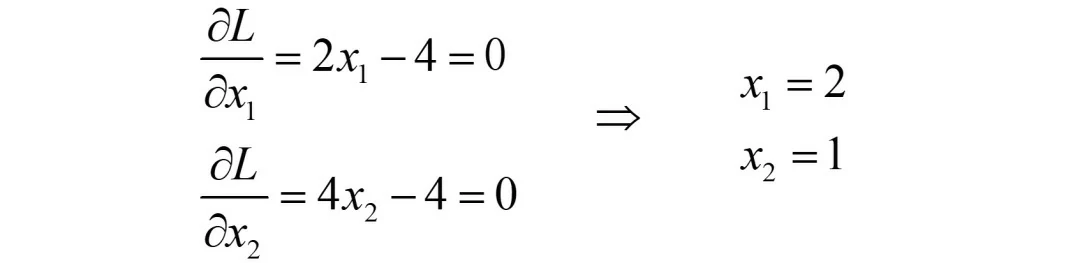
那x1=2,x2=1就是其中的一个解了吗?
赶紧背下口诀“等式求最优,不等式验证”!奥,原来还得验证下该解是否满足不等式g1<0和g2<0。
将x1=2, x2=1带入g1和g2,有:
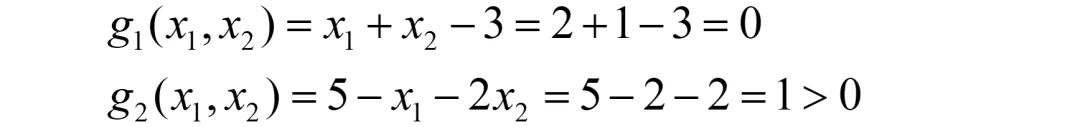
很遗憾,两个式子都无法使得 g1<0 和 g2<0,故只能舍弃该解。
此情形其实已经变为无约束问题(直接对f(X)求导后得到的解),然而它并不满足约束,只能舍弃。
同时也说明,最优解一定会在某个约束的边界上。那就继续吧,看看是在g1=0,还是g2=0,还是g1=g2=0的边界上。
(ii)若λ1=0, λ2>0,则g1<0, g2=0
除了两个求导后的方程,此情形多的两个方程分别为λ1=0和g2=0,故累计又有四个方程,求解有:
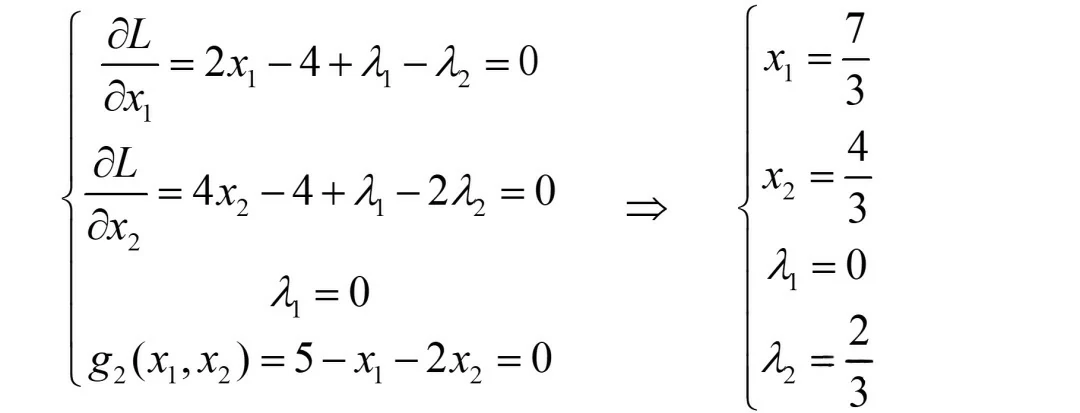
此时显然已经有λ2>0,故仅还需验证“g1<0”。
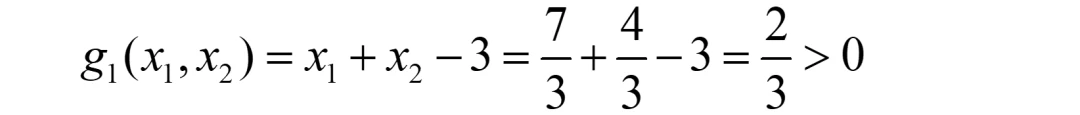
很可惜,不满足g1<0,故此解还是需要舍弃。
(iii)若λ1>0, λ2=0,则g1=0, g2<0
同2,也是四个方程,求解四个未知数,有:
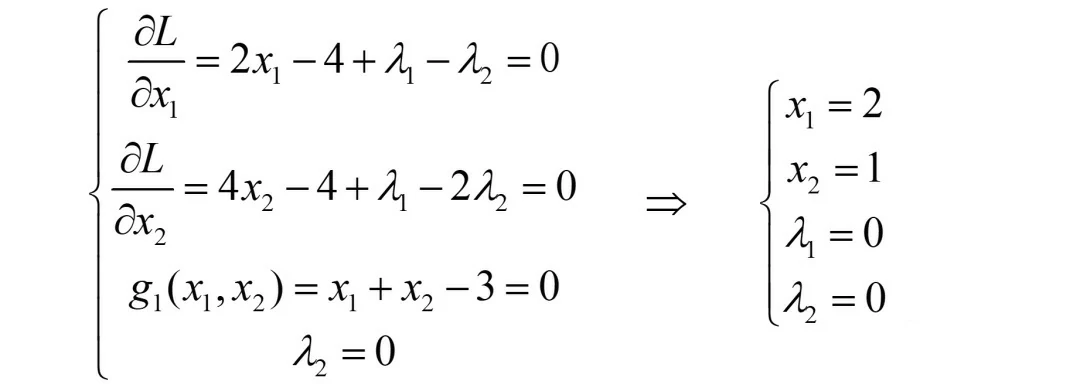
发现此解与情形1的解一样(仅是这个例子一样,一般不会一样),但带入g2函数时,有:
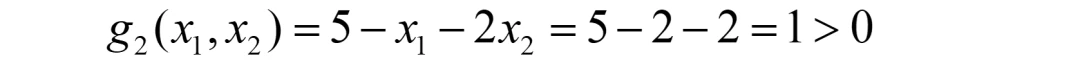
很可惜,依然不能使得g2<0,故该解还是需要舍弃。
(iv)若λ1>0, λ2>0,则g1=0, g2=0
此时,最优解在g1和g2函数的边界上,联立的四个方程为:
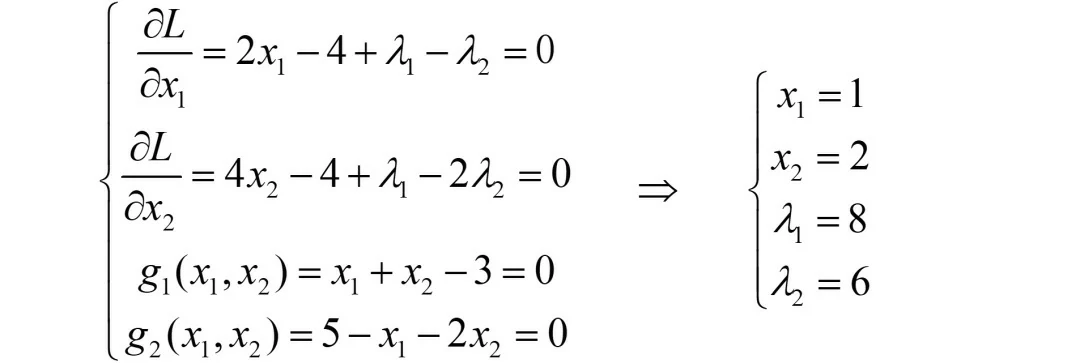
非常好,此时的λ1>0,λ2>0,满足KKT条件,故x1=1, x2=2是本题的最优解。
补充:一般四个方程,我是不会去手算的,编个简单的Matlab代码,就能快速求解:
1 | syms x1 x2 t1 t2 % t1,t2分别指λ1,λ2 |
其中,因为Matlab中不方便打λ,所以我一般用t来代替,同时解四个方程用“[]”框起来,四个变量也用“[]”框起来。“[]”在Matlab中一般用来表示数组或矩阵。solve函数就是解方程用的。
综上,x1=1, x2=2是本题的最优解。
符号运算实操
下面,实操下科研中遇到有不等式约束的极值问题时,该如何利用KKT条件,并采用Matlab来编码求解。算例如下:
无约束定价问题:
若企业生产成本为c的产品,市场需求函数为D = a - bp (a, b 是参数,p为价格),那企业的最优定价p为多少?
上面这个算例是无约束的,简单地再编两个约束吧,变为有不等式约束的问题:
有不等式约束的定价问题:
约束1(针对需求):假定需求量小于外生变量S;
约束2(针对价格):企业规定价格不能低于m*c(m>1);
则在这两个约束下,企业如何定价才能使利润最大?
先给出无约束问题下的解,决策最优定价p;再给出含有两个不等式约束的最优定价决策。
(i)无约束定价问题
此种情形较为简单,就是对利润函数(为二次函数)求最优值:
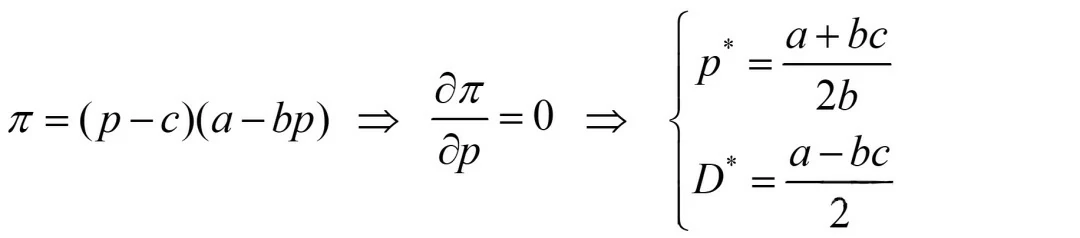
具体的Matlab计算代码如下:
1 | clear |
其中牵扯到的diff()、solve()、simplify()以及后面会提及的subs()函数,含义分别为求导、解方程、化简、替换。
(ii)有不等式约束的定价问题
这里新增了两个约束:
约束1(针对需求):假定需求量小于外生变量S:
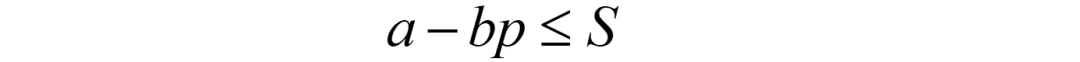
约束2(针对价格):企业规定价格不能低于m*c(m>1):
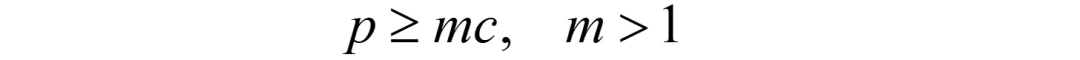
综上,我们有如下优化问题(写成最大化问题的标准形式):
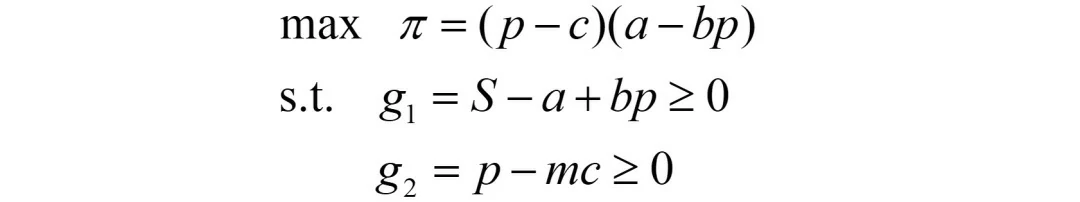
注意,这里与数值算例的最小化问题不同,该问题是最大化问题,因此需将约束全部转化为“≥0”的形式,并命名为g1、g2。
还记得第一步是什么吗?基于标准形式,构造拉格朗日函数:
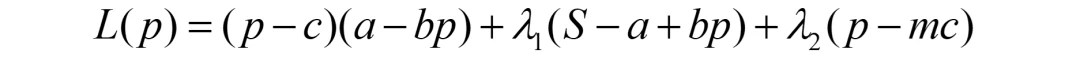
决策变量只有p,故仅对p求导即可:
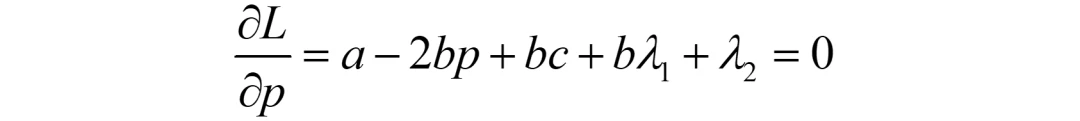
显然,这里仅有一个方程,要解出p、λ1、λ2三个未知数是不可能的,还需要两个等式方程。而KKT条件就是用来给出剩下的两个等式方程的。
这里附上上述过程的Matlab代码(为方便敲代码,依旧用t来代替λ):
1 | clear |
为方便后续计算,这里汇总下后面分类讨论时,会反复用到的几个表达式:
1 | clear |
综上,求导后的拉格朗日函数(Equ)含有p、λ1、λ2三个未知数,接下来分类讨论的目的,就是利用KKT条件,解这三个未知数。已经有Equ=0方程了,剩下的两个等式方程,分以下四种情况讨论吧。
情形1:若λ1=λ2=0,则g1>0,g2>0
注意,这里与第一部分数值算例中的“g1<0, g2<0”不同,这里是最大化问题。也许有同学已经发现了,这其实就是无约束问题(两个约束均没有起作用),得到的最优解即为之前的p*=(a+bc)/2b。
还记得口诀吗?等式求最优,不等式验证。所以,剩下的就是检验该解是否满足g1>0,g2>0。
因此,Matlab代码编写也分两步。先给出此种情形下如何计算最优p和最大利润,再计算得到该解需满足的条件。
1 | %% 情形1:当t1=t2=0时,g1>0, g2>0 |
时刻记住:在做符号运算时,求得的每一个解,都是有条件的。那么该解的条件是什么呢,就是g1>0,g2>0。既然S和m是我们新引进的参数,那么我们就来看看它俩需满足什么条件。
1 | % 将上述最优解代入g1,g2函数 |
代码中solve函数解出来的解,就是S和m需要满足的条件。
汇总下,就是只有当S和m满足如下条件时,才会得到如下最优解:
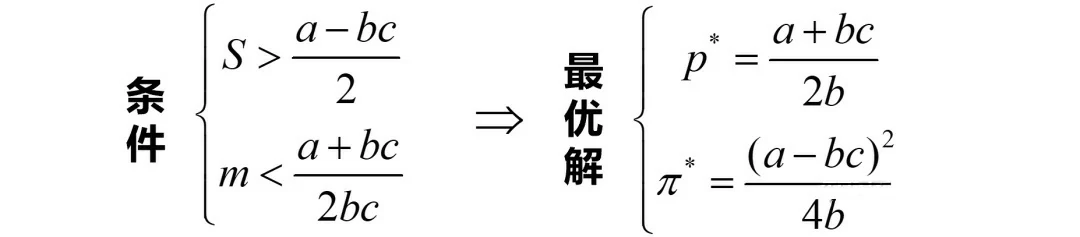
情形2:若λ1=0,λ2>0,则g1>0,g2=0
此时由于g2=p-mc=0,故最优解就是p*=mc;将其带入利润函数,便得到最优利润表达式。
当然,还需要看下想得到这个解,需要满足的条件,即:λ2>0,且g1>0。将λ1=0,p*=mc带入求导后的拉格朗日函数函数Equ,可以计算得到λ2的值,令其>0,加上g1<0的约束,便能最终该最优解适用范围。代码如下:
1 | %% 情形2:当t1=0,t2>0时,g1>0, g2=0 |
最后两行代码得到的解,就是为得到情形2下的最优解,需要满足的条件,汇总有:

情形3:若λ1>0,λ2=0,则g1=0,g2>0
此时由于g1 = S-a+bp = 0,故最优解就是p* = (a-S)/b;将其带入利润函数,便得到最优利润表达式。
再次回忆口诀:不等式验证。该情形还需要满足的条件,为:λ1>0,且g2>0。
将λ2=0,p* = (a-S)/b带入Equ,可以计算得到λ1的值,令其>0,加上g2>0的约束,便能最终该最优解适用范围。代码如下:
1 | %% 情形3:当t1>0,t2=0时,g1=0, g2>0 |
汇总代码计算结果,有:

情形4:若λ1>0,λ2>0,则g1=0,g2=0
该情形下的最优解就是求解三方程Equ=0,g1=0,g2=0下的p、λ1、λ2值。
由于两个约束都是关于p的一次函数,因此会得到矛盾的结论,故此种情形舍弃。
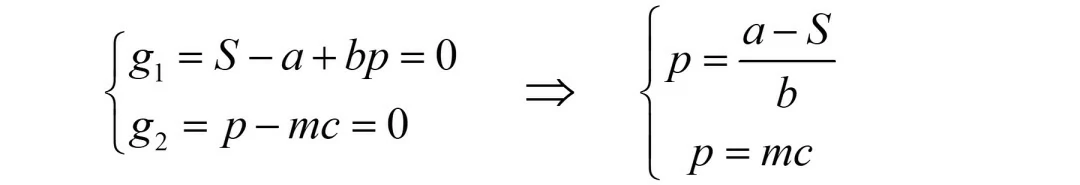
需要说明的是,科研中的很多问题会同时决策两个变量,或者有非线性的约束等,此时两个约束均取“=”是有解的。我这个算例编的简单了,造成该种情形无解。
(iii)最优值间的相互比较
上述4种情形,3种情形均有最优解。很显然,工作还没做完,我们真正想得到的是哪些参数条件下,最优定价和最大利润是多少?
如果是数值算例,很简单直观,拿着每种情形下的最大利润比较下即可。
但符号运算就不得不分类讨论,很多时候,我们甚至连某个表达式的正负号都无法确定。
但大家也不用太担心相互比较会很麻烦。因为,只看利润的话,真正需要比较的,其实只有情形2和情形3下的利润大小。聪明的你知道这是为什么吗?
答案揭晓:
情形1是无约束极值问题,相当于全域搜索最优解,其利润一定是最大的;情形2和3下的最优解,均受到了一个约束g=0的硬性限制,利润一定会小一点;而情形4限制更强,要求两个约束均为0,这样再去求利润,一定是最小的。
因此,在情形1的参数范围内,它就是老大,没必要跟它比了。所以,重点还是落在情形2和情形3的参数范围内,到底谁利润更大。
为方便阅读,避免前后翻看,情形2和情形3的结论汇总如下。

上述一通分析下来,其实也很简单嘛,将两利润做差,即Pi2 - Pi3,再看看正负号呗。
1 | % 比较情形2和情形3下的利润 |
这里用到了collect()函数,真的非常好用,大家一定要记住这个函数。
官方说collect是合并同类项函数,但我建议大家这样记忆:collect(f, x)就是将f函数以x的从高到低次项依次展开。如上述代码最后一行,就是以S的二次项,S的一次项,S的常数项依次展开。
这样有什么好处?那可太有用了,我们做科研时,一旦发现表达式是关于某参数的,3次甚至4次项后,建议换个参数或者换条思路求解吧。
因为求解三次函数的卡丹公式非常长,不适用于论文。而求解二次函数,韦达定理大家都是会的。
回到正文,观察差值del_Pi函数,是关于S的二次函数,开头向上,截距、对称轴均为正,且有两个解,分别为:
1 | solve(del_Pi, S); % 求解方程del=0的两个解 |
紧接着,这两个解谁大呢?再做差呗。看看和m的关系。
1 | del_S = S1 - S2; |
而 m > (a+b*c)/(2*b*c),恰好就是情形2下m的取值范围,故 S1 > S2。那基于此,我们可以画出del_Pi = Pi2 - Pi3的图像如下。
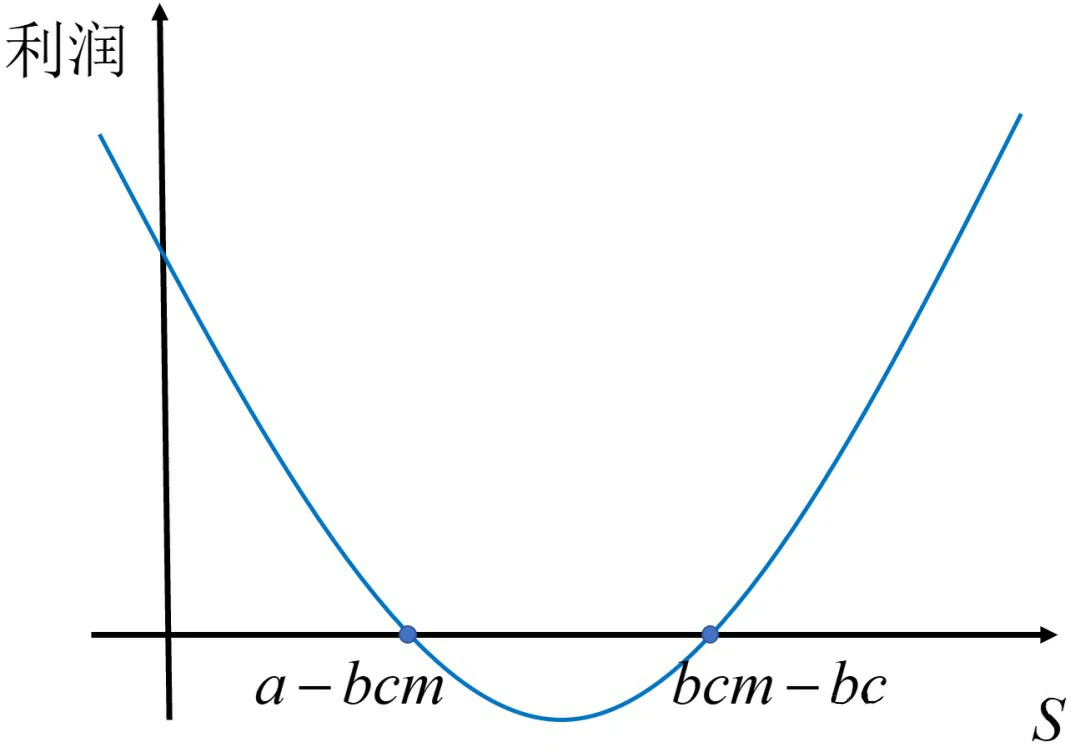
当0 < S < bcm-bc时,Pi2 < Pi3;
当bcm-bc < S < (a-bc)/2时,Pi2 > Pi3;
当(a-bc)/2 < S时,不用算了,Pi1最大。
细心的小伙伴也许会说,上面的第一个范围有问题。当 0 < S < a - bcm 时,不应该是 Pi2 > Pi3 吗?从图像上看,确实是的,但是别忘了,情形2中的 S 取值,是要“> a - bcm”的。所以当 0 < S < a - bcm 时,Pi2压根就没有图像。
至此,所有的问题就都分析完了。如果上述有错误,望大家批评指正。核心思想是会用KKT条件分类讨论,并会比较不同情形间的最优利润。
结语
总结下本文的核心:
- KKT条件是拉格朗日乘数法的推广,理解引入λi的原因及作用;
- 理解λg(X*)=0,就理解了KKT条件的精髓;
- 掌握采用图示法分析f(X)和g(X)的梯度关系。
- 数值算例中,在运用KKT条件时,很容易发现矛盾(不满足条件)的解,也很容易比较多个解的大小;
- 符号运算时,若不考虑参数范围,四种情形下的利润大小关系一定有:情形1 > 情形2、3 > 情形4;
- 比较利润大小时,最好寻求其关于某个参数的一次或二次函数关系,切忌使用高次项参数。
为了方便大家记忆KKT条件的求解步骤,编了个口诀,希望能对大家有所帮助:
大大小小
等式求最优,不等式验证
“大大小小”含义:在建立拉格朗日函数前,需要整理成标准形式。对于最大化问题,约束整理成“≥0”形式;对于最小化问题,约束整理成“≤0”形式。
别看写了不少,其实就记住这两行口诀就行。怎么样,是不是感觉KKT条件也不难嘛。
其实,还有拉格朗日乘子的敏感性分析没讲,这和对偶理论有关,篇幅有限,也较难,不再展开。