aoi学院

Aisaka's Blog, School of Aoi, Aisaka University

深度学习-CS231n Lecture 4 [2017版]

发表于 分类于 ， 阅读次数： Valine：
本文字数： 1.3k 阅读时长 ≈ 3 分钟
  • CS231n - Introduction to Neural Net

反向传播

计算图实例

  1. SVM
  2. AlexNet卷积神经网络
  3. 神经网络图灵机

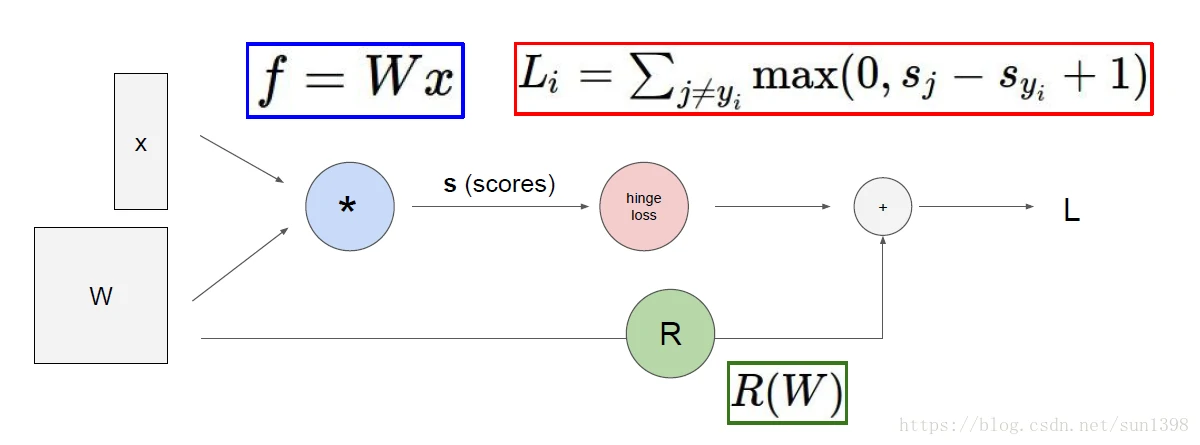
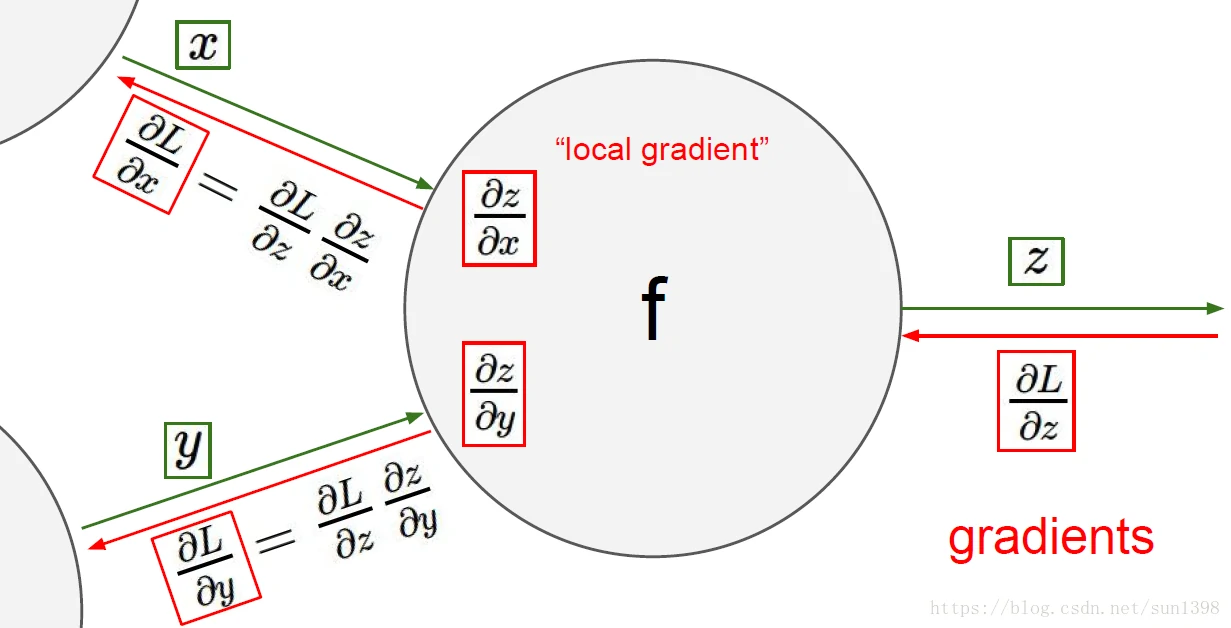
反向传播–链式求导法则（核心）

  1. 实例1：一个简单的计算
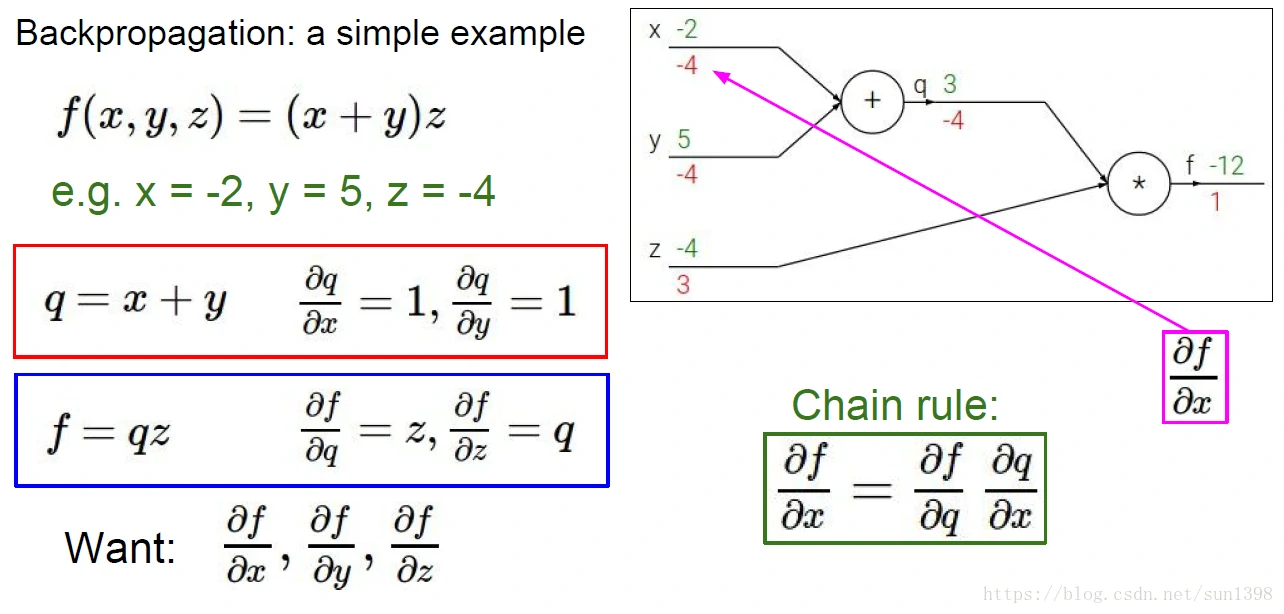
  1. 实例2：一个相对复杂的计算

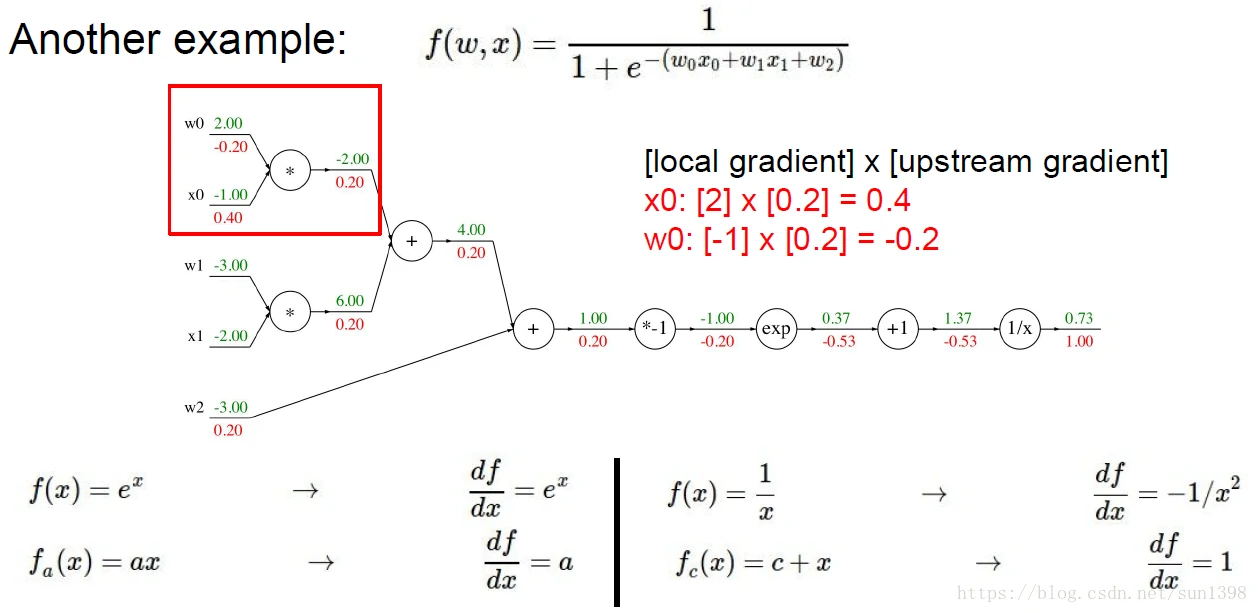
如果知道sigmoid函数的求导公式，那么可以极大地简化该过程

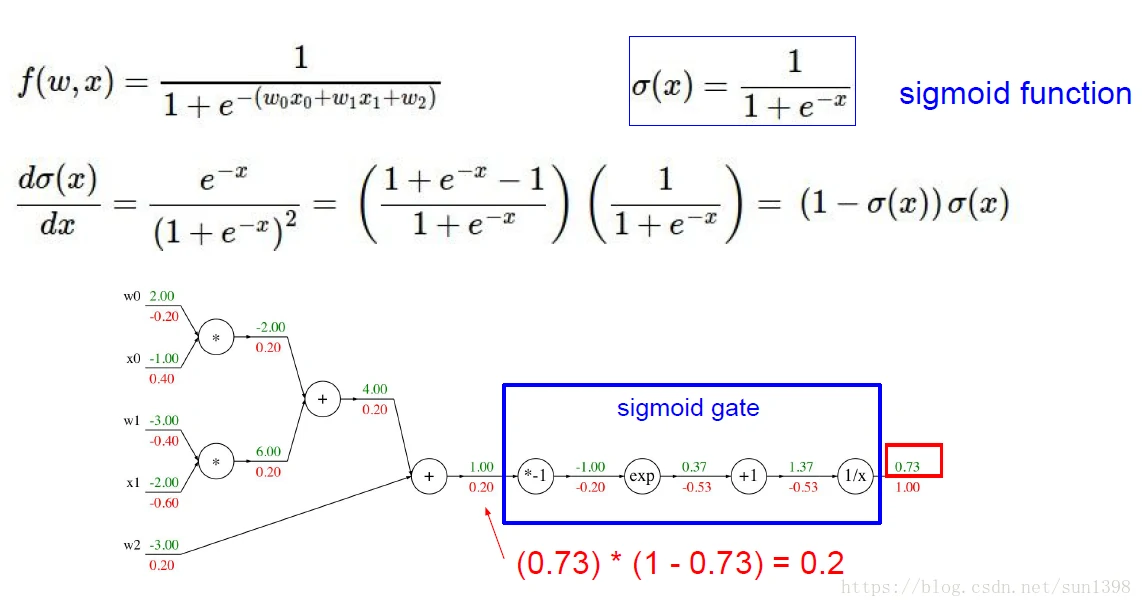
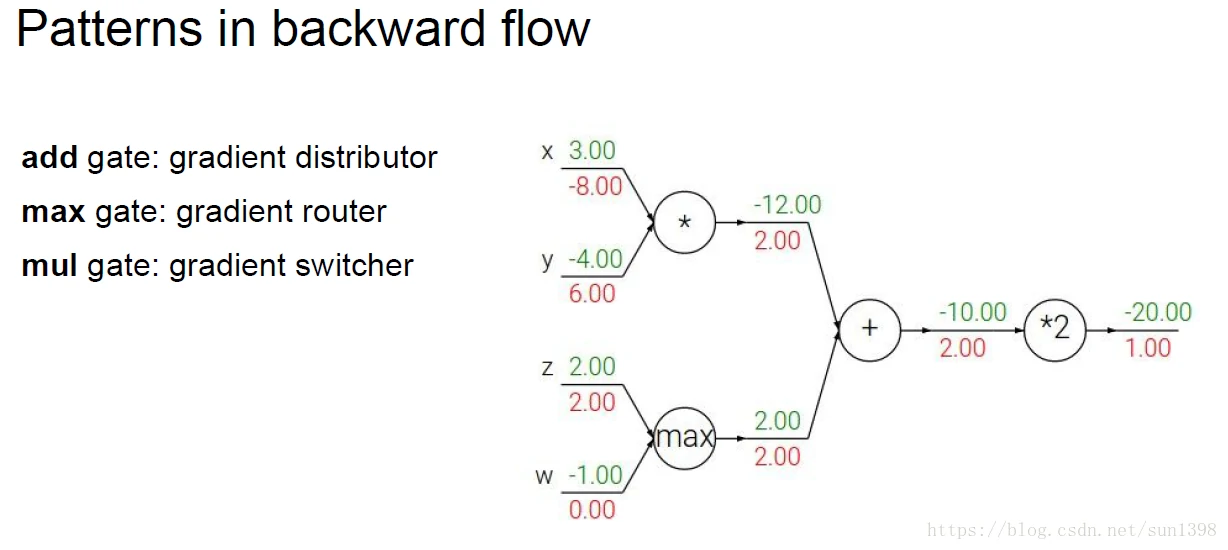
  1. 神经网络中的反向传播在分支处通过一级级的链式法则求导，使用当前已有的前后值替代。
  1. 反向传播在每一个分支点的操作：加法，分发下去；Max，路由选择，选中的相同，未选中的0；乘法，梯度转换。
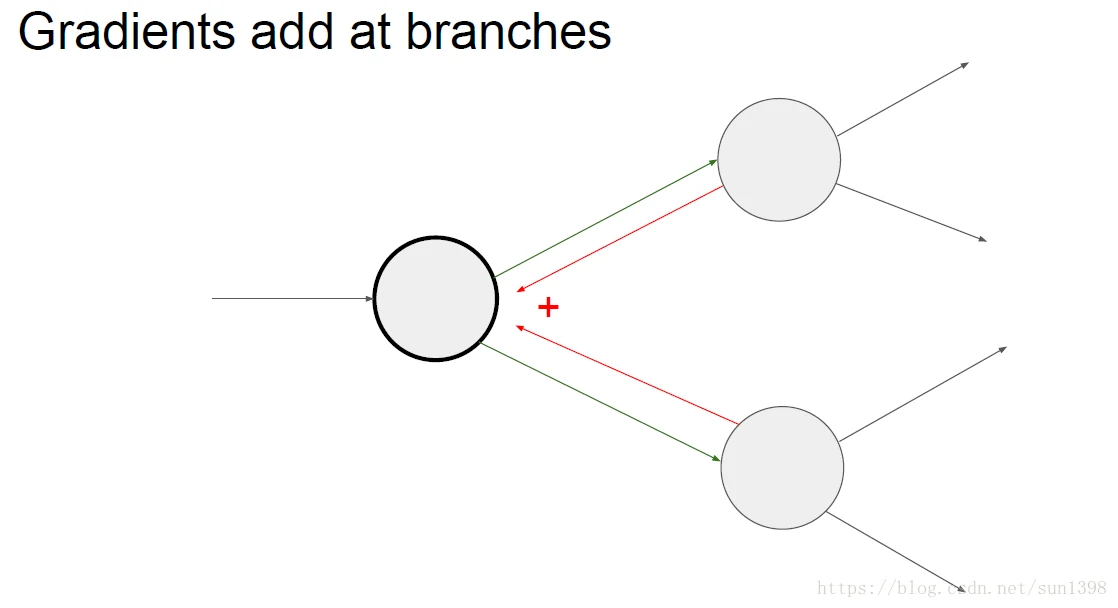
  1. 计算图向后分支的反向传播为相加

  1. 向量的梯度计算–雅克比矩阵逆推

    • 以max函数为例 实际上max函数的矩阵是一个单位矩阵上，在对角线上max取值正确的为1，错误的为0，反向求导赋予就很方便；因此不需要求雅克比矩阵的所有维度，实际上1个mini-batch的大小为100，矩阵可能为 409600 * 409600，这样一个维度较大，超出内存。实际上并不需要去求一个矩阵，见下面这个例子。
    • 以二次平方项为例 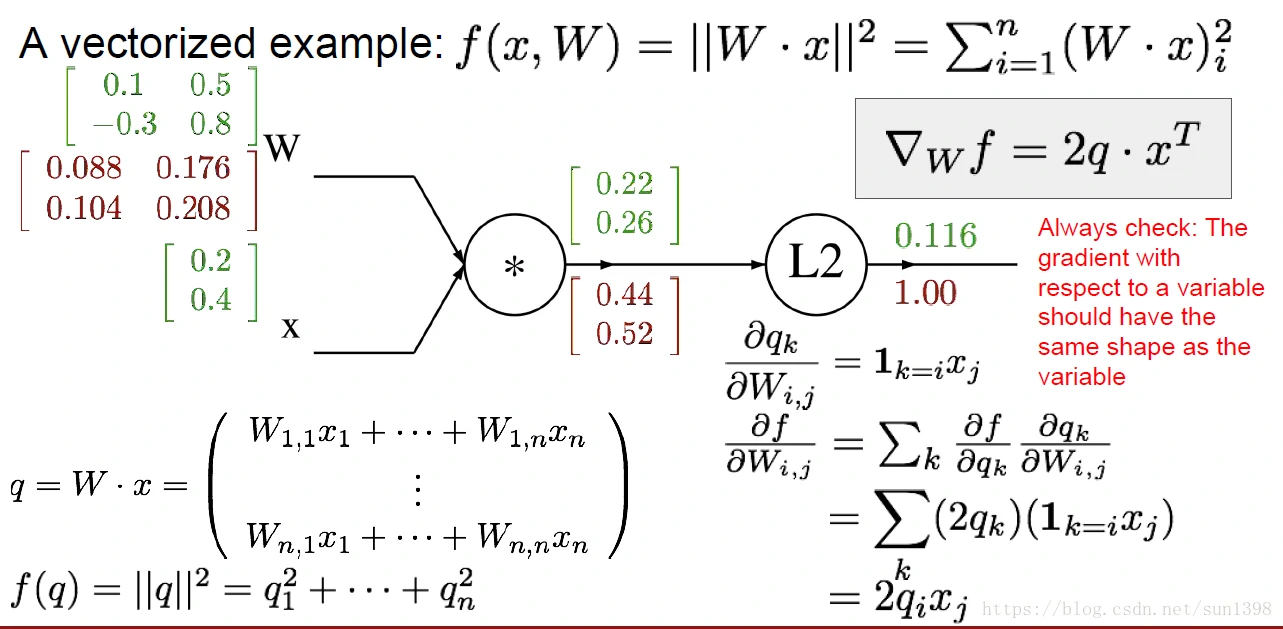如上图可见，实际上在反向传播过程，大部分使用的前向函数参数的转置就ok。

  2. 公式法+一步步逆推讲解矩阵乘法运算

实际上对于一个包含scores和loss函数的公式及求响应的∂L/∂W如下：

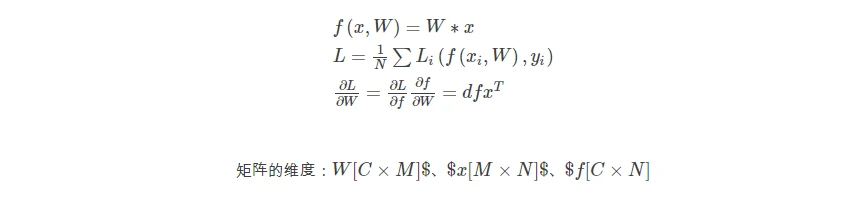
那么只对于单纯的一个f值而言，那么满足如下公式：

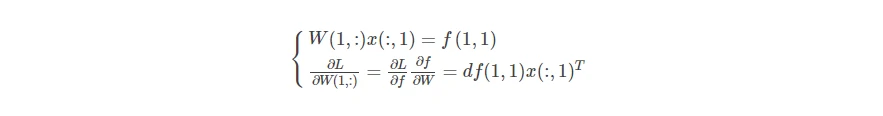
那么只对W(1,1)求导而言，f的所有1行都包含对W(1,1)与x一行的乘积，而f中的每个值都是W的一行和x的一列的乘积，无法单纯的表示w(1,1)，但是如果求df/dw(1,1)，由于线性其他项消失，只剩下x(1,:)，因此满足一下公式：

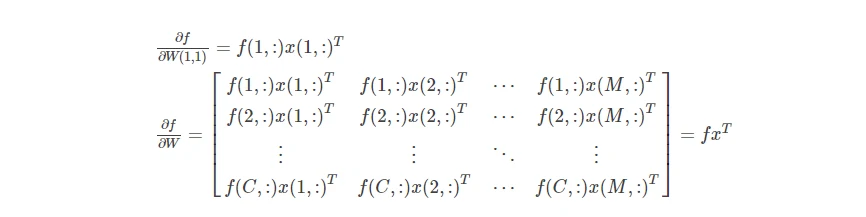
  1. SVM梯度函数推导过程

  2. Softmax梯度函数推导过程

  3. 系统结构与框架平台介绍

1
2
3
4
5
##SVM梯度矩阵表示
margin[margin>0] = 1 # 大于0返回真值
counter_r = np.sum(margin, axis=1)
margin[list(range(num_train)),y] = -counter_r
dW += np.dot(X.T,margin)/num_train +reg*W

2层神经网络

2层神经网络

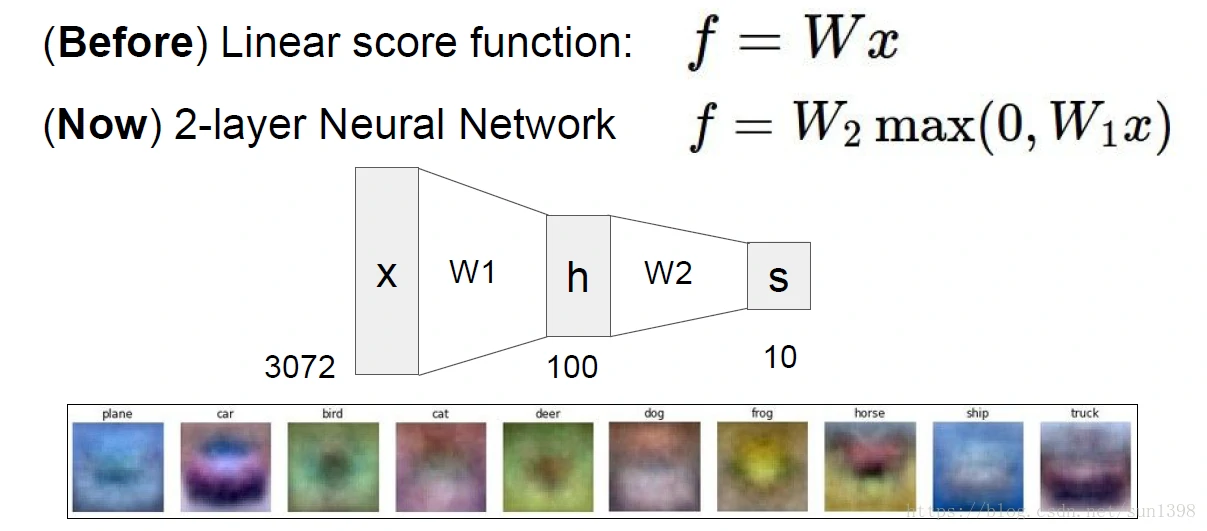
传统的1层神经网络能够对前面的图片进行h层的特征处理，第2层可以对经过h层的特征处理

一个2层神经网络的训练代码可能仅仅需要20行，具体的代码训练在assignment1中

一个神经网络与实际神经网络的关系，树突相当于每层的汇聚，轴突相当于激活后的传输：

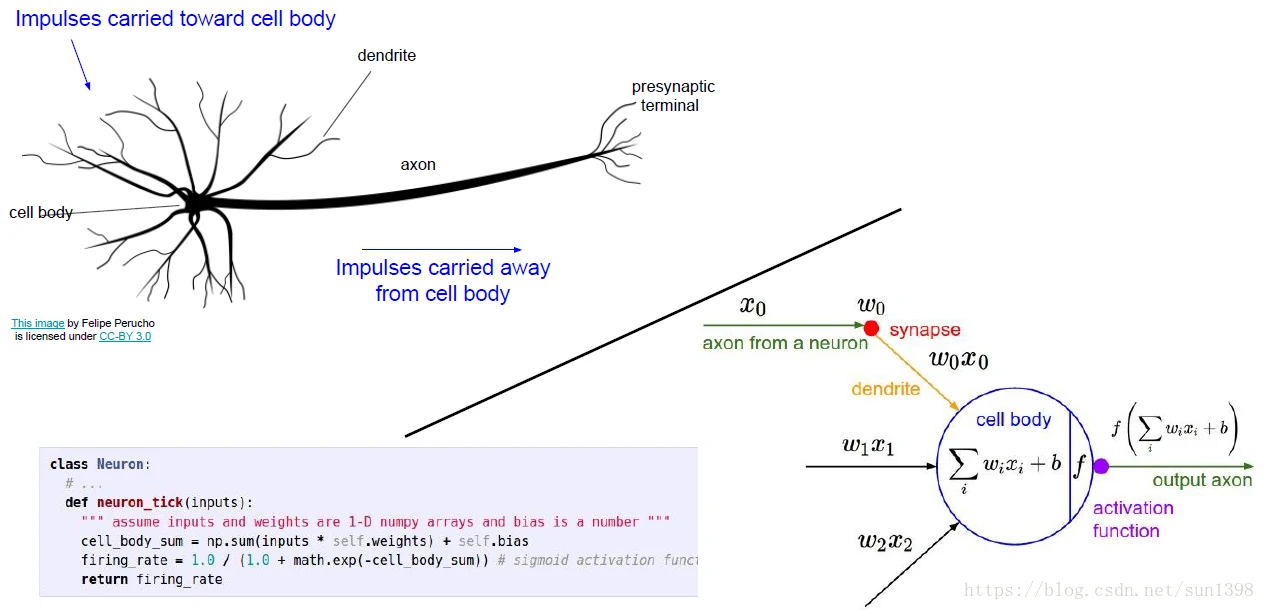
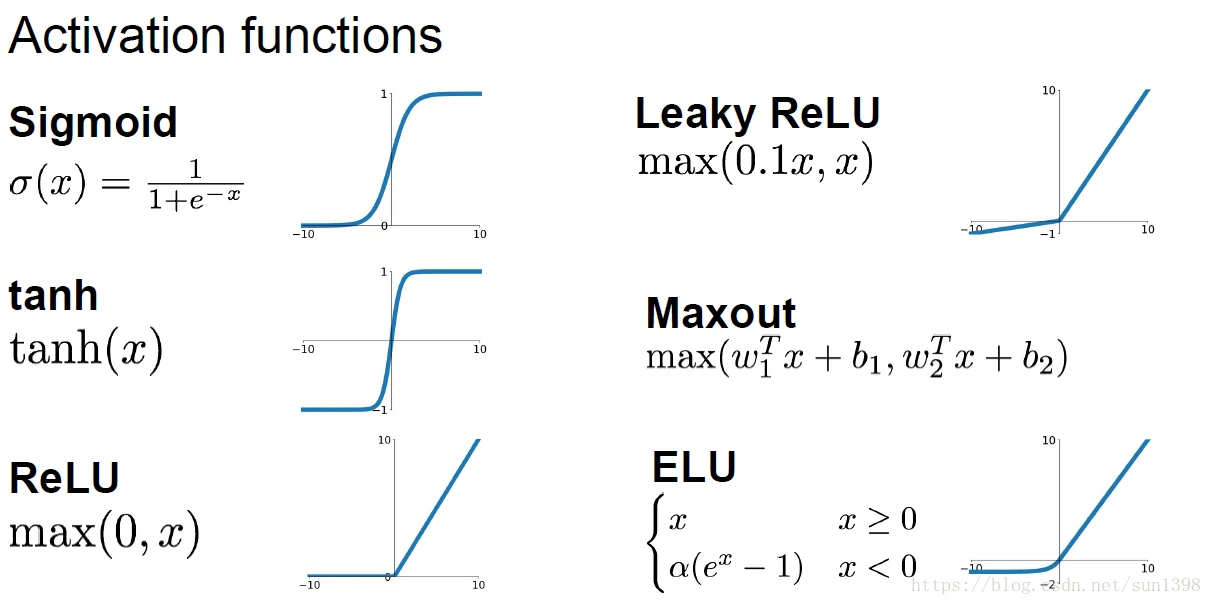
对于每一个神经元会使用激活函数，将线性的结果转换为[0,1]之间，有利于压缩结果的空间，因为实际上神经元识别是有上限的。常用的激活函数有：Sigmoid、Tanh、ReLU、LeakyReLU、Maxout、ELU，各有优缺点

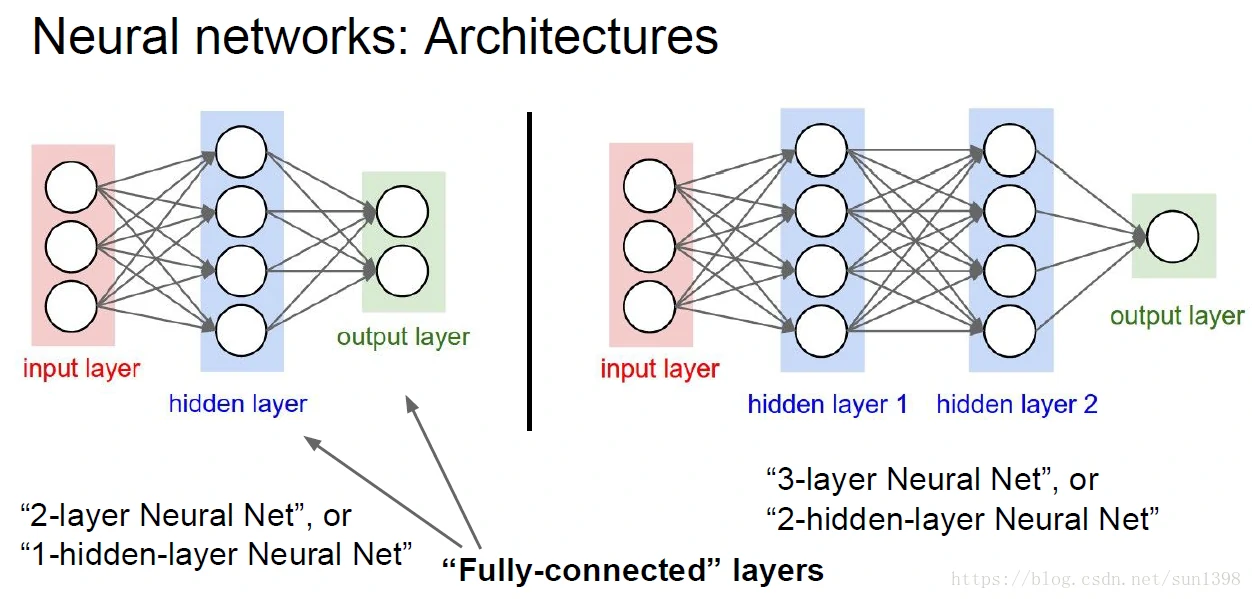
常见的2、3层神经网络结构如下：

总结

  • 神经网络不是真的神经元，是一种仿真的结果，或者说是给神经网络的结构一个合理的解释

  • 神经网络越大越好，层数越多越好，这个不完全成立，要看实际的情况。太大太深的网络容易过拟合（需要正则化），训练时间过长（无法解决）；当使用简单的数据时，深度起到的作用较少，每特征提取有限

  • 用好已有的框架结构，将会极大地减小工作量