本篇学习报告基于论文《Prototypical Networks for Few-shot Learning》,该论文的主要贡献有两点:(1)对图像领域的Few-Shot/Zero-Shot(小样本/零样本)任务,应用设计简单的原型网络方法(见第二部分),在通用数据集上达到了较好的实验效果(见第三部分);(2)对原型网络本身进行了较为深入的分析,且分析了距离度量方式的选择对任务效果的影响(见图3)。 原文链接及开源代码已置于文末。
概述
在小样本分类问题中,最需要解决的一个问题是数据的过拟合问题。由于训练数据过少,一般的分类算法会表现出过拟合的现象,从而导致分类结果与实际结果有较大的误差。为了减少因数据量过少而导致的过拟合的影响,可以使用基于度量的元学习方法,该论文所提出的原型网络便属于这种方法。
该论文为解决小样本分类问题提出了原型网络。在训练集中,对于每一种出现的类别,只给出少量样本,但分类器能够很好的泛化到其他没有出现于训练集中的新类别。原型网络会学习一个度量空间,在该空间中,可以通过计算与每个类的对应原型表示的距离来进行分类,距离哪个类的原型表示最近,则被判断为哪个类。与最近的小样本学习方法相比,该方法反映了一种更简单的归纳偏差,有利于在这种有限的数据范围内使用,并取得优异的效果。论文表明一些简单的设计决策比最近涉及复杂体系结构选择和元学习的方法可以产生较好的改进效果。
介绍两类常见的Few-Shot方法:
- 匹配网络(Matching Network):
可以理解为在embedding空间中的加权最近邻分类器。模型在训练过程中通过对类标签和样本的二次采样来模仿Few-Shot任务的测试场景,学习一个匹配网络。该网络只在训练集中的关系基础上训练,并且直接应用于测试集中的关系。原型网络也属于一种匹配网络。实验和总结中将对原型网络和匹配网络的不同之处和分类效果进行比较。- Optimization-based meta-learning:
这种方法在训练的过程中的目标是学习如何通过少量样本更好的拟合数据,因此该类方法会针对测试数据集对网络进行调整。例如,在训练过程中,利用LSTM的网络结构学习每个训练step所需要的学习率。
方法解析
在该论文所提出的原型网络方法中,需要将样本投影到一个度量空间,且在这个空间中同类样本距离较近,异类样本的距离较远。下图为这个投影空间的示意图,假如在这个投影空间中,存在三个类别的样本,且相同类别的样本间距离较近。为了给一个未标注样本x进行标注,则将样本x投影至这个空间并计算x与各个类别的原型距离,离得近的就认为x属于哪个类别。
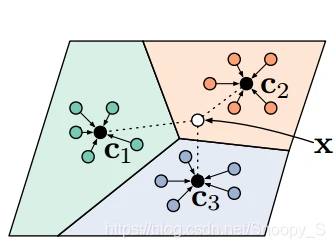
那么,现在有几个问题:
- 怎么将这些样本投影至一个空间且让同类样本间距离较近?
- 怎么说明一个类别所在的位置,从而能够让未标记的样本计算与类别的距离?
如何将样本投影至一个空间且让同类样本间距离较近?论文中使用的是一个带参数φ的嵌入函数fφ(x),这个函数可以理解为投影的过程,x表示样本的特征向量,函数值表示投影到那个空间后的值,这个嵌入函数fφ(x)是一个神经网络,参数φ是需要学习的,可以认为参数φ决定了样本间的位置,所以需要学习到一个较好的φ值,让同类别样本间距离较近。
此外,还需要考虑如何说明一个类别所在位置,论文中认为一个类的位置由这个类所有样本在投影空间里的平均值决定,类k的原型表示公式如下:
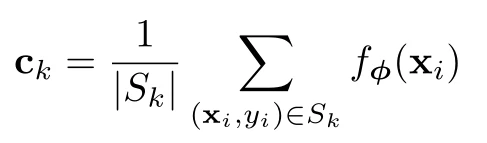
其中Sk表示类k,|Sk|表示类k中样本的数量,(xi , yi)为样本的特征向量和标记,此公式实际上为一个求平均的过程。
得到每个类的原型后,就需要根据样本与各个类的原型的距离,求一个样本属于一个类的概率。因为在训练时这个样本是已标记的,即我们已知类k的原型,已知一个属于类k的样本,求此样本属于类k的概率,因此我们的目标函数就是求这个概率的最大值。
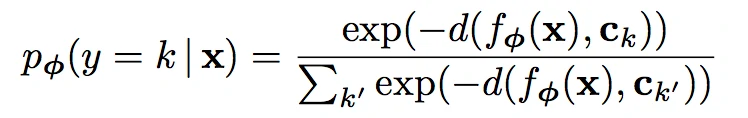
此公式所表示的意义是,对于样本x,求它到每个类的距离,然后进行归一化操作得到概率,即x属于类k的概率。其中d为距离函数,在本篇论文中使用的是欧几里得距离。在训练过程中,x的标签是已知的。论文中的目标函数为:
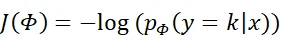
一般通过随机梯度下降方法来求它的最小值,从而收敛后学到一个好的φ值。可以认为,训练结束后此投影函数可以将同类的样本投影到一个相互距离较近的地方。
字符说明:
N:训练集中样例的数量
K:训练集中类的数量
NC:每个Episode中类别的数量
NS:每个类中支持样例的数量
NQ:每个类中查询样例的数量
以下Algorithm 1给出了计算训练集损失J(Φ)的伪代码

计算过程:为Episode选择类别 → 选择支持集 → 选择训练集 → 计算支持集的原型 → 初始化损失 → 更新损失
在测试过程中,使用与训练过程中相同的投影函数方法,求每个类的原型,根据一个未标记的样本x,求属于每个类的概率,认为概率值大的那个,即为x属于的类别。
总结原型网络的基本思想:基于集群,找到类的原型,找到合适距离度量方式进行分类。
实验
说明
实验的数据分为支持集和查询集:
支持集:即训练集,在该论文中由一些已标记的样本组成,比如有N个类,每个类中有M个样本,则为N-way–M-shot。
查询集:即测试集,在该论文中由一些已标记的样本和部分未标记的样本组成,后续实验结果表明训练集的way大于测试集的话分类结果更好(我认为这有助于提高模型的泛化性),而shot最好一致(我认为是为了保持不同类别样本的平衡性)。
Omniglot分类
Omniglot是一个1623个手写字符分类的数据集。每一个字符类别只有20个样本,不同样本由不同的人绘制。
该论文使用原形网络在Omniglot数据集上进行实验,使用欧几里得距离作为距离度量,分别在1-shot和5-shot进行实验。下图为某个子集的度量空间的可视化,其中黑色点代表每种类别的原形,红色代表被错误分类的数据,红色箭头的指向为真实的类别。
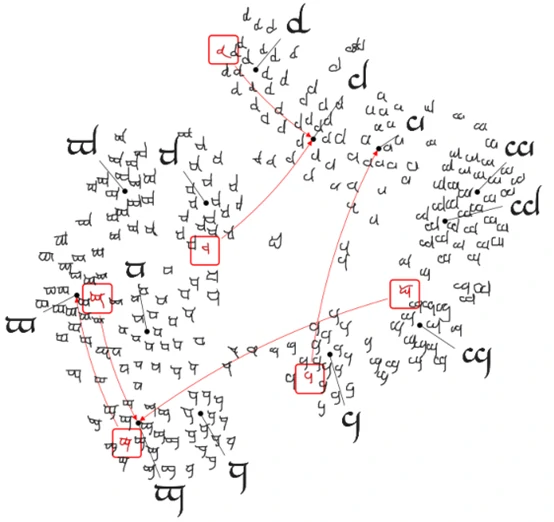
训练episode的设置为60个类别和每个类别有5个query查询点。实验结果发现在训练和测试时保持相同的样本数据量(即shot相同)和episode使用更多的类别(即way更大)会使得实验效果更好。下表展示的是该论文所提出的方法与其他方法在Omniglot数据集上的结果对比。
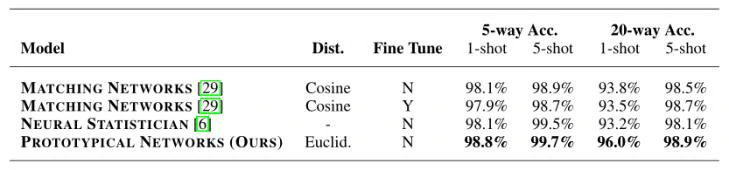
miniImageNet分类
minilmageNet数据集包含100个类别,每个类别中包含600个样本数据。其中64个类别数据作为训练集,16个类别数据作为验证集,20个类别数据作为测试集。
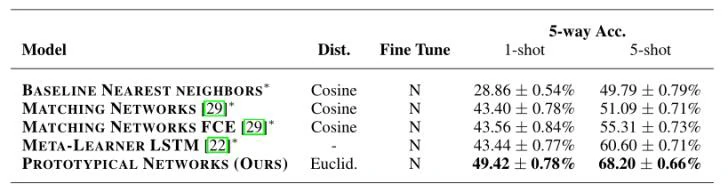
实验分别对1-shot和5-shot的设置进行训练episode为5-way和20-way的训练,实验结果表明也训练episode中设置更多的类别,对实验的结果有一定的增益效果,这是因为更大的way设置有助于网络进行更好的泛化,使得模型在度量空间做出更细粒度的决策。
还有个比较有意思的实验结果:在N-way M-shot问题中的M=1,也就是one-shot的情况下,prototype network实际上等价于matching network;此外,无论是one-shot还是M-shot(M>1),欧氏距离(Euclid.)的效果都要比余弦距离(Cosine)的效果好(如下图所示),因此本文使用的距离计算公式为欧氏距离。
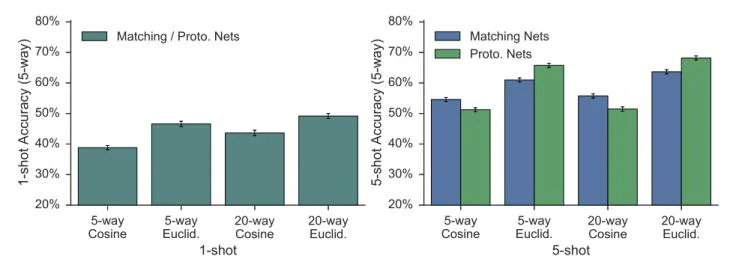
总结分析
本论文提出的Prototypical Networks(P-net)思想与Matching Networks(M-net)十分相似,两种网络主要有以下不同点:
- 使用了不同的距离度量方式,M-net中是余弦距离,P-net中使用的是属于布雷格曼散度的欧几里得距离。
- 二者在few-shot的场景下不同,在one-shot时等价(one-shot时取得的原型就是支持集中的样本,相当于不用进行平均处理)
- 网络结构上,P-net将编码层和分类层合一,参数更少,训练更加方便。
论文的实验部分中也在不同数据集上进行了两种网络的效果比较,结果显示P-net的效果要优于M-net。本论文提出的原型网络方法虽然结构设计比较简单,但是却能达到很好的效果,这为我们在解决小样本分类问题时提供了一种可行的解决思路。
参考链接
https://www.scholat.com/teamwork/showPostMessage.html?id=9855