什么是范数
我们知道距离的定义是一个宽泛的概念,只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念,它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解,我们可以把范数当作距离来理解。
在数学上,范数包括向量范数和矩阵范数,向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是,对应向量范数,向量空间中的向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小,就好比米和尺都可以来度量远近一样;对于矩阵范数,学过线性代数,我们知道,通过运算AX=B,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
向量的范数表示这个原有集合的大小。
矩阵的范数表示这个变化过程的大小的一个度量。
简单说:L0范数表示向量中非零元素的个数(即为其稀疏度),L1范数表示为绝对值之和,而L2范数则指模。
向量范数
L-P范数
x 的 n 范数:x 到零点的 n 阶闵氏距离。即向量元素绝对值的p次方和的1/p次幂
根据P的变化,范数也有着不同的变化,一个经典的有关P范数的变化图如下:
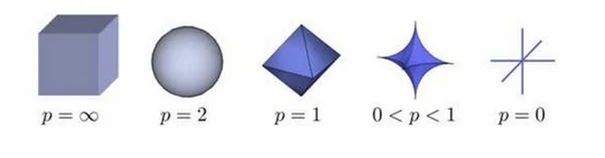
实际上,在0时,Lp并不满足三角不等式的性质,也就不是严格意义下的范数。
0-范数
x 的 0 范数:x 到零点的汉明距离。表示向量 x 中非零元素的个数。
当P = 0时,也就是L0范数,L0范数并不是一个真正的范数,它主要被用来度量向量中非零元素的个数。
对于L0范数,其优化问题为:
在实际应用中,由于L0范数本身不容易有一个好的数学表示形式,给出上面问题的形式化表示是一个很难的问题,故被人认为是一个NP难问题。所以在实际情况中,L0的最优问题会被放宽到L1或L2下的最优化。
1-范数
x 的 0 范数:x 到零点的汉明距离。表示向量 x 中非零元素的绝对值之和。
L1范数有很多的名字,例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference):

对于L1范数,它的优化问题如下:
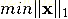
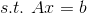
由于L1范数的天然性质,对L1优化的解是一个稀疏解,因此L1范数也被叫做稀疏规则算子。通过L1可以实现特征的稀疏,去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高体重等可能都是无用的,利用L1范数就可以过滤掉。
2-范数
x 的 2 范数:x 到零点的欧氏距离。Euclid范数(欧几里得范数,常用计算向量长度),表示向量元素的平方和再开平方。
L2范数是我们最常见最常用的范数了,像L1范数一样,L2也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference):
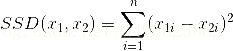
对于L2范数,它的优化问题如下:
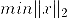
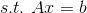
L2范数通常会被用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂造成过拟合的情况,从而提高模型的泛化能力。
∞-范数
x 的无穷范数:x 到零点的切比雪夫距离。即所有向量元素绝对值中的最大值/最小值
矩阵范数
1-范数
列和范数,即所有矩阵列向量绝对值之和的最大值
2-范数
谱范数,即AᵀA矩阵的最大特征值的开平方(λ为AᵀA的最大特征值)
∞-范数
行和范数,即所有矩阵行向量绝对值之和的最大值
F-范数
Frobenius范数,即矩阵元素绝对值的平方和再开平方
核范数
即奇异值之和(λᵢ是A的奇异值)
机器学习中的范数
在很多机器学习相关的著作和教材中,我们经常看到各式各样的距离及范数,如:∥𝓍∥、∥𝑿∥,其中,𝓍 和 𝑿 分别表示向量和矩阵。
与L0范数相关
在诸多机器学习模型中,比如压缩感知(compressive sensing),我们很多时候希望最小化向量的L0范数。然而,由于L0范数仅仅表示向量中非0元素的个数,因此这个优化模型在数学上被认为是一个NP-hard问题,即直接求解它很复杂、也不可能找到解。需要注意的是,正是由于该类优化问题难以求解,因此压缩感知模型是将L0范数最小化问题转换成L1范数最小化问题。
与L1范数相关
L1范数优化问题比L0范数优化问题更容易求解,借助现有凸优化算法(线性规划或是非线性规划),就能够找到我们想要的可行解。鉴于此,依赖于L1范数优化问题的机器学习模型如压缩感知就能够进行求解了。
正则项与稀疏解
在机器学习的诸多方法中,假设给定了一个比较小的数据集让我们来做训练,我们常常遇到的问题可能就是过拟合 (over-fitting) 了,即训练出来的模型可能将数据中隐含的噪声和毫无关系的特征也表征出来。
为了避免类似的过拟合问题,一种解决方法是在 (机器学习模型的) 损失函数中加入正则项,比如用L1范数表示的正则项,只要使得L1范数的数值尽可能变小,就能够让我们期望的解变成一个稀疏解 (即解的很多元素为0)。
如果我们想解决的优化问题是损失函数 f(𝓍) 最小化,那么,考虑由L1范数构成的正则项后,优化目标就变成:
尽管类似的优化模型看起来很“简练”,在很多著作和教材中也会加上这样一句说明:
1 | 只要优化模型的解 𝓍 的 L1范数比较小,那么这个解就是稀疏解,并且稀疏解可以避免过拟合。其中,“稀疏”一词可以理解为 𝓍 中的大多数元素都是0,只有少量的元素是非0的。 |
可能比较难理解,接下来做简要说明,为了理解L1范数的正则项和稀疏性之间的关系,我们可以想想下面三个问题:
- 为什么L1范数就能使得我们得到一个稀疏解呢?
- 为什么稀疏解能够避免过拟合?
- 正则项在模型中扮演者何种角色?
什么是过拟合问题?
假设我们现在买了一个机器人,想让它学会区分汉字,例如:

认定前5个字属于第一类,后5个字属于第二类。在这里,10个字是所有的训练“数据”。如果机器人很聪明,它能够把所有的字都“记住”,看过这10个字以后,机器人学会了一种分类的方式:它把前5个字的一笔一划都准确地记在心里。只要我们给任何一个字,如“揪”(不在10个字里面),它就会很自信地告诉你,非此即彼,这个字属于第二类。机器人没见过这个字,它将这个字归为第二类,这可能就错了。
因为我们可以明显看到,前5个字都带提手旁。所以,“揪”属于第一类。机器人的失败在于它太聪明,而训练数据又太少,不允许它那么聪明,这就是过拟合问题。
正则项是什么?为什么稀疏可以避免过拟合?
其实可以让机器人变笨一点,希望它不要记那么多东西。
还是给它前面测试过的那10个字,但现在机器人已经没办法记住前5个字的一笔一划了(存储有限),它此时只能记住一些简单的模式,于是,第一类字都带有提手旁就被它成功地发现了。
实际上,这就是L1范数正则项的作用。L1范数会让你的模型变傻一点,相比于记住事物本身,此时机器人更倾向于从数据中找到一些简单的模式。
机器人原来的解:[把, 打, 扒, 捕, 拉]
机器人变傻以后的解:[扌, 0, 0, 0, 0]
比较正式的解释如下:
假设我们有一个待训练的机器学习模型:A𝓍 = b
其中, A 是一个训练数据构成的矩阵, b 是一个带有标签的向量,这里的 𝓍 是我们希望求解出来的解。
当训练样本很少 (training data is not enough)、向量 𝓍 长度很长时,这个模型的解就很多了。
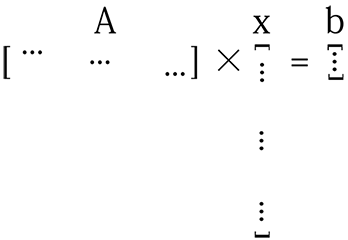
如图,矩阵 A 的行数远少于向量 𝓍 的长度。
我们希望的是找到一个比较合理的解,即向量 𝓍 能够发现有用的特征 (useful features)。使用L1范数作为正则项,向量 𝓍 会变得稀疏,非零元素就是有用的特征了。
当然这里也有一个比较生动的例子:
1 | Suppose you are the king of a kingdom that has a large population and an OK overall GDP, but the per capita is very low. Each one of your citizens is lazy and unproductive and you are mad. Therefore you command “be productive, strong and hard working, or you die!” And you enforce the same GDP as before. As a result, many people died due to your harshness, those who survived your tyranny became really capable and productive. [example] |
如果把总人口总量视作向量 𝓍 的长度,那么优胜劣汰其实相当于增加了一个正则项。在稀疏的结果中,我们能够保证向量 𝓍 的每个元素都是有用的!
到这里,我们知道了为什么稀疏可以避免过拟合。
为什么增加L1范数能够保证稀疏?
根据L1范数的定义,向量的L1范数是所有元素的绝对值之和,以向量 [x, y]ᵀ 为例,其L1范数为 |x| + |y|
选取两个向量:x1 = [0.1, 0.1]ᵀ 、 x2 = [1000, 0]ᵀ
其中,x1很明显不是一个稀疏向量,但其L1范数∥x1∥ = |0.1| + |0.1| = 0.2 却远小于稀疏向量x2的L1范数∥x2∥ = |1000| + |0| = 1000
仅仅是看L1范数的数值大小,我们可能很难比较向量的稀疏程度,因此,需要结合损失函数。
再回到前面的问题:A𝓍 = b,在平面直角坐标系上,假设一次函数 y = ax + b 经过点(10, 5) ,则
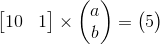
由于 b = 5 - 10a ,所以参数a, b的解有无数组 (在蓝线上的点都是解)。
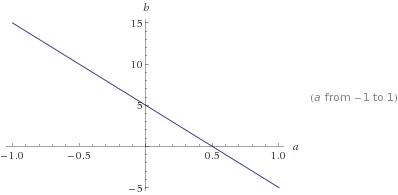
怎样通过L1范数找到一个稀疏解呢?
我们不妨先假设向量的L1范数是一个常数c ,如下图:
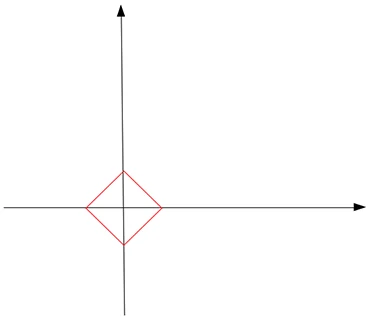
它的形状是一个正方形 (红色线),不过在这些边上只有很少的点是稀疏的,即与坐标轴相交的4个顶点。
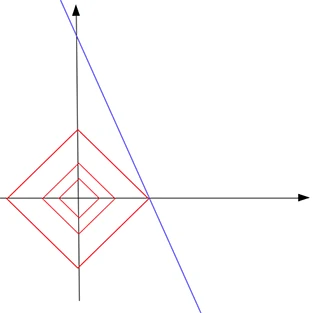
把红色的正方形(L1范数为常数)与蓝色的线 (解) 放在同一个坐标系,于是,我们发现蓝线与横轴的交点恰好是满足稀疏性要求的解。同时,这个交点使得L1范数取得最小值。
最简单的最小二乘线性模型
最开始,最小二乘的loss(需优化的目标函数)如下:
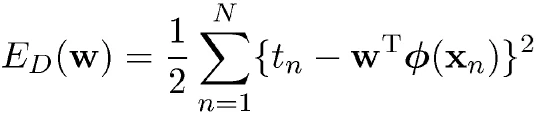
式中,tn是目标变量,xn是观测量(自变量),Φ是基函数(后期推导与核化相关),是w是参数。此式有闭式解,解为:
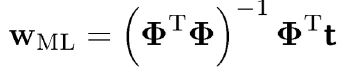
但是我们都知道,矩阵求逆是一个病态问题,即矩阵并不是在所有情况下都有逆矩阵。所以上述式子在实际使用时会遇到问题。为了解决这个问题,可以求其近似解。可以用SGD(梯度下降法)求一个近似解,或者加入正则项(L2范数)。加入正则项是我们这里要说的。加入L2范数的正则项可以解决这个病态问题,并且也可以得到闭式解,在实际使用时要比用SGD快,并且加入正则化后的好处并不仅仅是这些。加入正则项(L2范数)的loss如下:
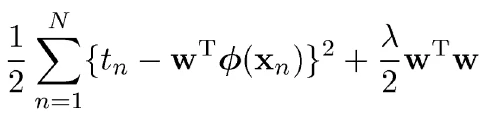
其闭式解为:
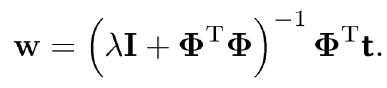
此式在 λ 不为零时,总是有解的,所以是一个非病态的问题,这在实际使用时很好。除了这一点,2范数的正则项还有其他好处,比如控制方差和偏差的关系,得到一个好的拟合,这里就不赘述了,毕竟这里讲的是范数,有兴趣可以参阅相关资料。
加入正则项后一般情况下的loss为:
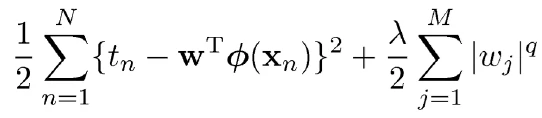
好了,我们终于可以专注于范数了。不同范数对应的曲线如下图:
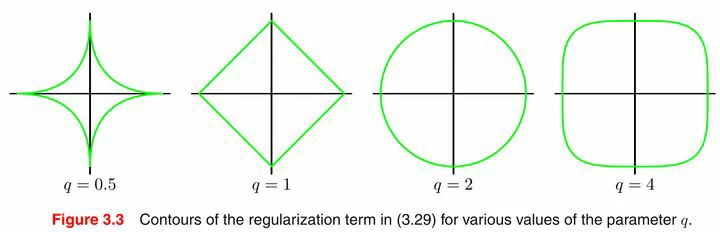
上图中,可以明显看到一个趋势,即q越小,曲线越贴近坐标轴,q越大,曲线越远离坐标轴,并且棱角越明显。q = 0 和 q = ∞ 时极限情况如下:
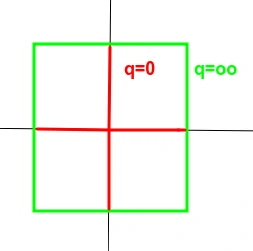
除了图形上的直观形象,在数学公式的推导中,q = 0 和 q = ∞ 时两种极限的行为可以简记为非零元的个数和最大项。即L0范数对应向量或矩阵中非零元的个数,无穷范数对应向量或矩阵中最大的元素。
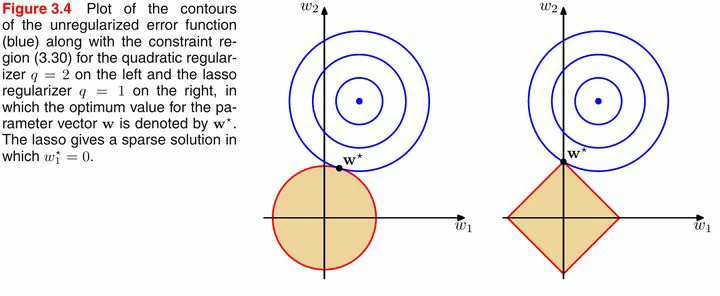
上图中,蓝色的圆圈表示原问题可能的解范围,橘色的表示正则项可能的解范围。而整个目标函数(原问题+正则项)有解当且仅当两个解范围相切。从上图可以很容易地看出,由于L2范数解范围是圆,所以相切的点有很大可能不在坐标轴上,而由于L1范数是菱形(顶点是凸出来的),其相切的点更可能在坐标轴上,而坐标轴上的点有一个特点,其只有一个坐标分量不为零,其他坐标分量为零,即是稀疏的。
所以有如下结论,L1范数可以导致稀疏解,L2范数导致稠密解。那么为什么不用L0范数呢,理论上它是求稀疏解最好的规范项了。然而在机器学习中,特征的维度往往很大,解L0范数又是NP-hard问题,所以在实际中不可行。但是用L1范数解是可行的,并且也可以得到稀疏解,所以实际稀疏模型中用L1范数约束。
至此,我们总结一下,在机器学习中,以L0范数和L1范数作为正则项,可以求得稀疏解,但是L0范数的求解是NP-hard问题; 以L2范数作为正则项可以得到稠密解,并且由于其良好的性质,其解的定义很好,往往可以得到闭式解,所以用的很多。
另外,从距离的角度说一下范数。1范数对应街区距离,2范数对应大家熟知的欧式距离,无穷范数对应棋盘距离(切比雪夫距离)。


参考资料
https://blog.csdn.net/a493823882/article/details/80569888
https://www.zhihu.com/question/20473040
https://zhuanlan.zhihu.com/p/26884695
https://blog.csdn.net/susanzhang1231/article/details/52127011