SphereFace(超球面)是佐治亚理工学院Weiyang Liu等在CVPR2017.04发表,提出了将Softmax loss从欧几里得距离转换到角度间隔,增加决策余量m,限制||W||=1和b=0,SphereFace: Deep Hypersphere Embedding for Face Recognition
主要思想
- 开集人脸识别:测试图像没有在训练集中出现过,是度量学习问题,学习有判别力的大间隔特征。
- A-Softmax loss(Angular Softmax loss):使CNN能够学习角度识别特征,引人了角度间隔m,以使人脸特征的最大类内距离要小于最小类间距离,使学习的特征将更具有判别力。
- L-Softmax loss、A-Softmax loss、CosFace、ArcFace、COCO loss、Angular Triplet Loss等都是angular margin learning系列
- 预处理(人脸对齐):人脸关键点由MTCNN检测,再通过相似变换得到了被裁剪的对齐人脸。
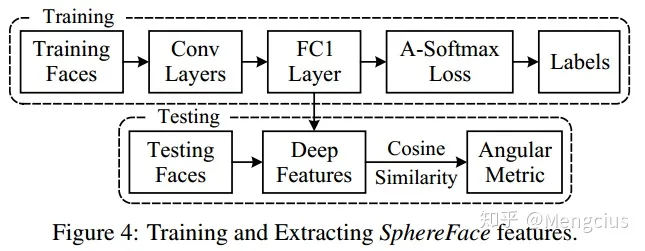
- 训练(人脸分类器):CNN + A-Softmax Loss,CNN使用使用ResNet中的残差单元
- 测试:从人脸分类器FC1层的输出中提取表示特征SphereFace,拼接了原始人脸特征和其水平翻转特征获得测试人脸的最终表示;对输入的两个特征计算余弦距离,得到角度度量。
- 人脸验证:用阈值判断余弦距离。
- 人脸识别:最近邻分类器。
- LFW上99.42%,YTF上95.0%,训练集使用CASIA-WebFace。2017年在MegaFace上识别率在排名第一。
SphereFace学习和推理
- 预处理(人脸对齐):人脸关键点由MTCNN检测,再通过相似变换得到了被裁剪的面。RGB图像中的每个像素([0,255])通过减去127.5然后除以128进行标准化。
- 训练:CNN + A-Softmax Loss
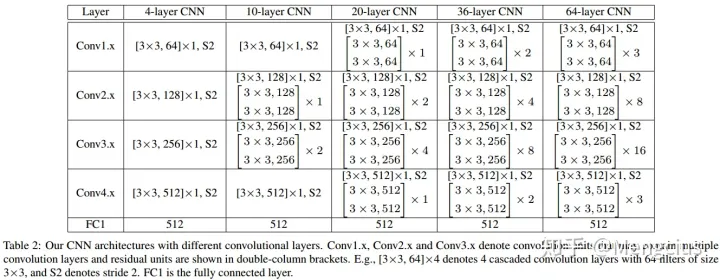
- CNN框架与传统的方法相同,因此它可与任何先进的网络架构兼容(如VGG/ GoogLeNet/ResNet等),这里使用ResNet中的残差单元,如表2用不同深度(4、10、20、36、64)的CNN来评估
- 使用了Angular Softmax loss,使学习的特征将更具有判别力,使m=4。
- 测试:
- 从FC1层的输出中提取深层特征人脸表示(SphereFace)。在所有实验中,测试人脸图像的最终表示是通过连接其原始脸部特征和水平翻转特征来获得的。
- 对两个特征计算余弦距离(Cosine Similarity),得到角度度量(Angular Metric)。
- 人脸验证:用阈值判断上面算的余弦距离。
- 人脸识别:最近邻分类器。
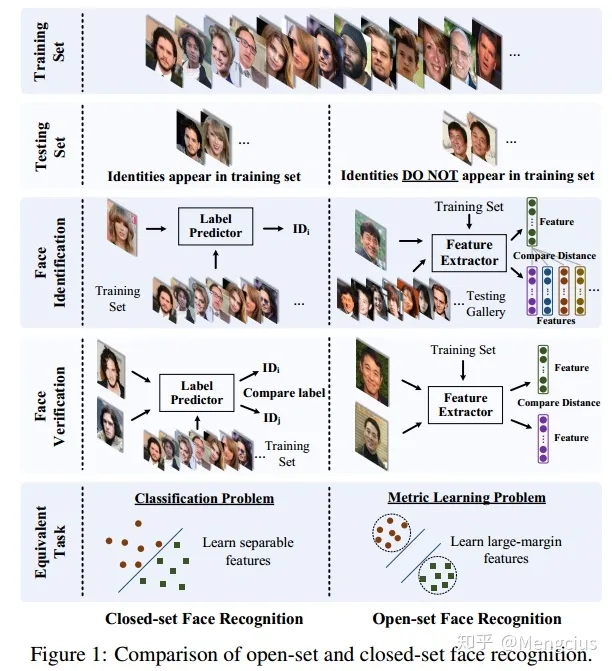
开集人脸识别(Open-set face recognition)
- 通常,人脸识别可分为人脸识别和人脸验证。前者将一个人脸分类为一个特定的标识,而后者确定一对图片是否属于同一人。
- 闭集(open-set)是测试图像在训练集中可能出现过;开集(close-set)是测试图像没有在训练集中出现过。开集人脸识别比闭集人脸识别需要更强的泛化能力。过拟合会降低性能。
- 闭集的人脸识别:相当于分类问题,学习可分离的特征就可以了,人脸验证或识别时提取出标签。所有测试标识都在训练集中预先定义。很自然地将测试人脸图像分类为给定的身份。在这种情况下,人脸验证相当于分别对一对人脸图像进行识别。
- 开集的人脸识别:测试集通常与训练集分离,因为不可能将所有人脸图像归纳在一个训练集中,我们需要将人脸映射到一个可辨别的本地特征空间。在这种情况下,人脸识别被视为在输入人脸图片和数据库中的每个身份之间执行人脸验证。它是度量学习问题,关键是学习有判别力的大间隔特征(discriminative large-margin features),人脸验证或识别时都要比较特征间的距离。
- Open-set FR对特征要求的准则:在特定的度量空间内, 需要类内的最大距离小于类间的最小距离。
度量学习
- 度量学习(metric learning):旨在学习一个相似的(距离)函数。传统的度量学习常常会学习一个距离度量矩阵A ,在给定的特征x1,x2上距离度量为:
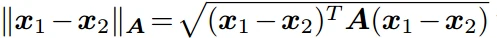
- 最近流行的深度度量学习通常使用神经网络自动学习具有可区分性的特征x1,x2,然后是简单的进行距离度量,如欧几里得距离。用于深度度量学习的最广泛的损失函数是对比损失和三元组损失,两者都对特征施加了欧几里得距离。
分析其他算法的度量学习
- DeepFace、DeepID:通过SoftMax Loss学习面部特征,但只具有可分离性而不具有明显的可判别性。
- DeepID2:结合了softmax loss和contrastive loss以增强特征的判别能力。但它们产生不同的特征分布,softmax损失会产生一个角度的特征分布,对比损失是在欧几里得空间学习到的特征分布,所以特征结合时可能不是一个自然的选择。
- FaceNet:使用Triplet loss来监督嵌入学习。但它需要非常大量数据(2亿张人脸图像),计算成本很高。对比损失和三元组损失都不能限制在单个样本上,因此需要精心设计的双/三重挖掘过程,这既耗时又对性能敏感。
- VGGFace:先训练CNN+Softmax loss,再用Triplet loss度量学习。
- A discriminative feature learning approach for deep face recognition. In ECCV2016:将Softmax loss与Center loss结合以增强特征的判别能力,但中心损失只起到缩小类间距离的作用,不具有增大类间距离的效果。
- L-Softmax loss(作者和A-softmax loss是同一批人)也隐含了角度的概念。利用改进的softmax loss进行具有角度距离的度量学习。作为一种正则化方法,它在闭集分类问题上显示了很大的进步。A-softmax loss简单讲就是在Large-Margin Softmax Loss的基础上添加了两个限制条件||W||=1归一化和b=0,使得预测仅取决于W和x之间的角度。
人脸识别的DCNNs有两个主要的研究方向:分类学习(softmax loss)、度量学习(triplet loss等)。contrastive loss、triplet loss等都将开集人脸识别问题视为度量学习问题,对比损失和三元组损失都是基于欧几里得距离的度量学习。
Softmax损失学习按角度分布的特征
- Softmax损失可以自然地学习按角度分布的特征,如在训练集和测试集不同类别的特征只在角度上分离开,因此不会自然地促使包含任何欧几里德损失。
- 从某种意义上说,基于欧几里德距离的损失与softmax损失是不相容的,因此将这两种类型的损失结合起来并不是很好。
- 学习特征时增大欧几里得距离,似乎是广泛认可的选择,但问题出现了:欧几里得距离是否总是适合于学习具有可判别性的面部特征?不适合,本文建议用角度距离代替。
- 为什么用角度间隔?
- 首先角度间隔直接与流形上的区别性联系在一起,流形上的区别性本质上与前面的一致,面也位于流形上。其次,由原始Softmax loss获得的特征具有固有的角分布,将角度间隔与Softmax loss结合起来实际上是更自然的选择。
- 首先,它们只将欧几里得距离强加于学习到的特征,而我们的则直接考虑角度间隔。第二,contrastive loss、 triplet loss 在训练集中构成成对/三重集时都会受到数据扩展的影响,而我们的则不需要样本挖掘,并且对整个小批量都施加了可判别性约束(相比之下,对比损失和三重损失只会影响几个具有代表性的成对/三重集)。
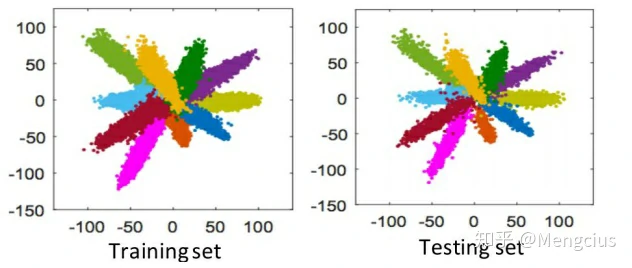
Softmax Loss的进化(二元分类举例)
原版的Softmax Loss
- Softmax计算两个类的概率为:
- x为学习到的特征向量,Wi和bi是最后一个全连接层对应类i的权值和偏置。
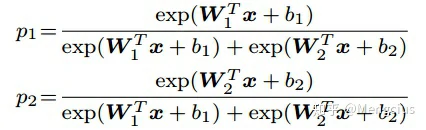
- Softmax损失的决策边界(decision boundary)是(就是刚让两类分开的边界,如p1=p2):
- 需要p1>p2来正确分类x
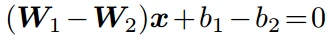
- Softmax loss,重写成w和x的内积形式,就有了cos夹角:
- θji是向量Wj和xi之间的夹角
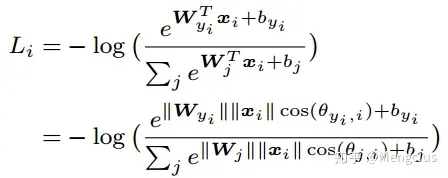
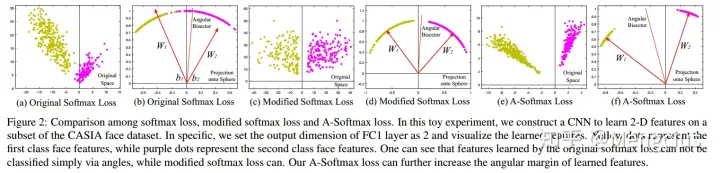
- 学习到的特征分布投射到一个球体上,就可以看到两类别间不能简单地通过角度分类。两类别是可以分离开的,但还是有一些误差,Softmax只学习到了可分离的特征,但内聚性不好,判别性不够。如a b
Modified Softmax Loss
- Modified softmax loss能够直接优化角度,使CNN能够学习角度分布特征。
- 为了实现角度决策边界,最终FC层的权重实际上是无用的。因此,首先对权重进行归一化并将偏置项归零(||W_i||=1,b_i=0),后验概率为p_1=||x||cos(θ_1),p_2=||x||cos(θ_2),则决策边界变为:
- 结果仅取决于θ_1和 θ_2,需要cos(θ_1)>cos(θ_2)来正确分类x
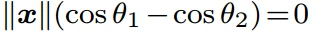
- 虽然我们可以用这个改进的softmax loss来学习带有角边界的特征,加强了角度可分性,但是这些特征还是没有判别性(discriminative)。如图c d
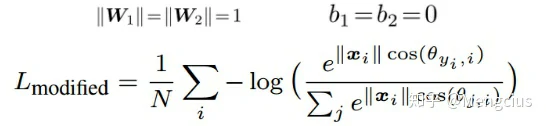
A-Softmax Loss
- 进一步引入角度间隔(angular margin),让分类更加困难从而学习判别性。角度间隔更加大了,但分布的弧长变短了。如e f
- A-Softmax loss(Angular Softmax loss)针对不同的类别采用不同的决策边界(每个边界都比原边界更严格),从而产生角间隔。
- 引入一个整数m来定量控制决策边界,二分类的类1和类2的决策边界分别变为:
- 从类别1正确分类,需要cos(mθ_1)>cos(θ_2),决策边界就是cos(mθ_1)=cos(θ_2)。从类别2的则相反。从角度的观点来考虑,从标识1正确分类x需要mθ_1<θ_2,而从标识2正确分类x需要mθ_2<θ_1。
- 因为m是正整数,cos函数在0到π范围又是单调递减的,所以mθ_1要小于θ_2,m值越大,θ_1应越聚合,则学习的难度也越大,因此通过这种方式定义损失会逼得模型学到类间距离更大的,类内距离更小的特征。
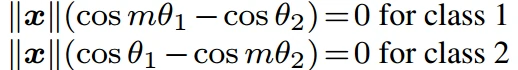
- A-Softmax loss公式是将改进的Softmax Loss中θ乘以系数m整数间隔值。即以乘法的方式惩罚深度特征与其相应权重之间的角度。
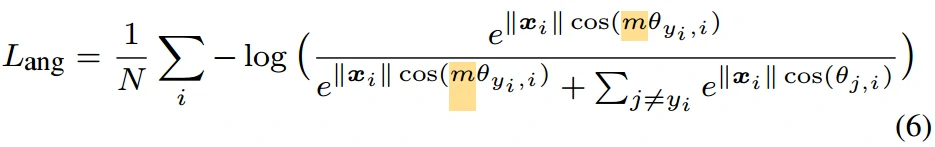
- A-Softmax Loss最终公式:上式中θ的范围是[0, π/m],为了摆脱这一限制,我们将cos(mθ, i)推广到一个单调递减的角函数ψ(θ,i)。m≥1是控制角度间隔大小的整数,当m=1时它就是Modified Softmax Loss。请注意,在每次迭代中权重归一化为1。
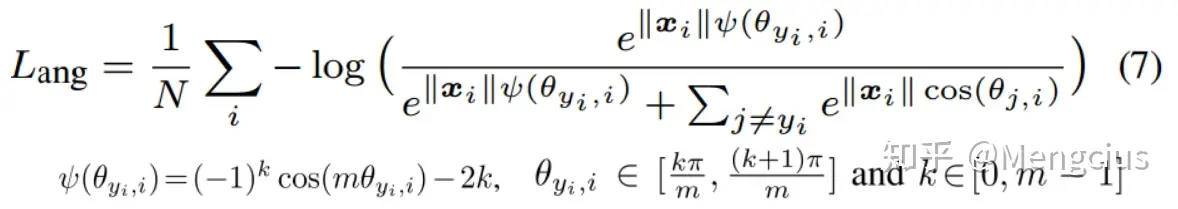
- 它们的决策边界:
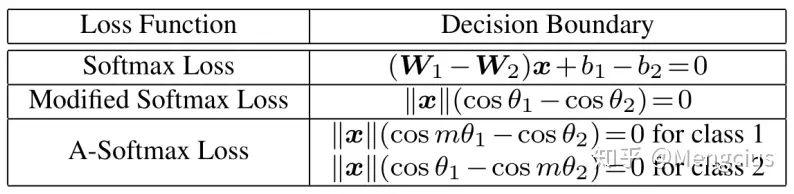
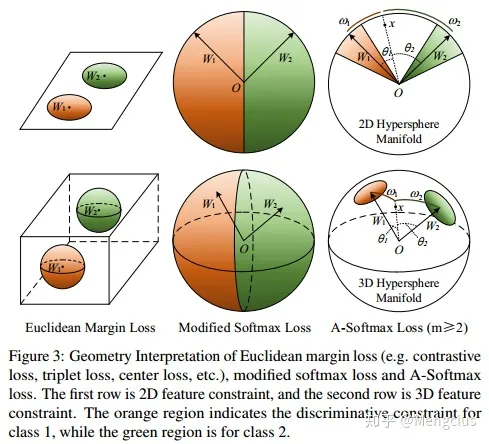
几何上观察
几何上, A-Softmax损失可被视为对超球面流形施加判别约束:
- 欧几里德间隔损失 Euclidean Margin Loss (如对比损失、三重损失、中心损失等)对类别的约束,在2D下是两个有距离间隔的圆,在3D下是两个有间隔的球。
- Modified Softmax Loss的两类之间并没有间隔,分布弧长很大
- A-Softmax损失在2D情况下对单位圆施加弧长约束,两类间有角度间隔,在3D情况下对单位球上的圆状区域约束,就有了类间距离间隔(m-1)*θ/(m+1)。
- 颜色阴影代表了密密麻麻的样本特征点,最近的一对不同类特征点应该满足m*θ_1<θ_2。图中标的θ可能是个均值
A-Softmax Loss的性质
- 属性1:A-Softmax损失定义了一个可调节难度的大角度间隔(large angular margin)学习任务。随着m越大, 角度间隔变大,流形上的约束区域θ1变小,相应的学习任务也变得更加困难,学习到的特征判别性越好。
- 定义1:特征分布的最小m_min是最小值,当m>m_min时A-SoftMax loss 定义了一个学习任务,其中最大类内角度特征距离被限制为小于最小类间角度特征距离。
- 属性2:二元分类情况下m_min的下界是m_min≥2+√3 。推导公式如下:
二分类中,设W1、W2分别是类别1与类别2的权重,W1与W2之间的夹角是θ12,输入的特征为x,那么权重W与输入特征x之间的夹角θ就决定了输入的特征属于那个类别,因为判断概率要p1>p2,则要cos(mθ_1)>cos(θ_2),一般可以认为输入的特征输于类别1,则要满足mθ1<θ2。当没有m时,θ1夹角应该小于θ2夹角才能正确判断为类别1,乘个m倍就是要让θ1更加小时才能正确判断,即让θ1更加聚合。
1)由 m*θ1=θ2 求出这时θ1的最大值θ_max1(类内最大间隔),求出类间最小角度间隔θ_inter。
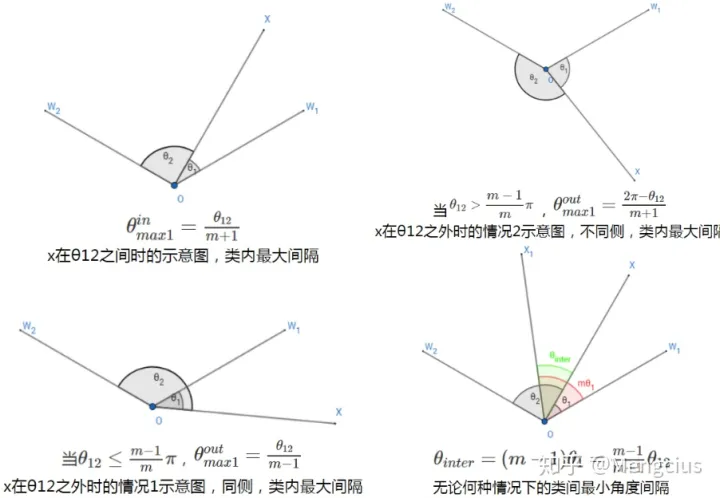
2)再根据最大类内特征角度距离小于最小类间特征角度距离,以上的分析可以总结为公式(8)(9),解两不等式可以得到m_min≥2+√3。
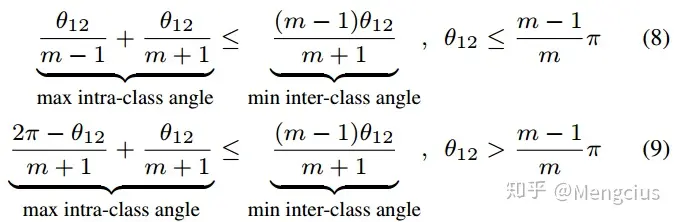
属性3:多元分类情况下,假设在欧几里德空间中均匀分布,m_min的下界是 m_min>=3。推导公式如下:

- 基于此,我们使用m=4来近似期望的特征分布准则。实验还表明,m越大越好,但m=4通常就足够了。
A-Softmax与L-Softmax的区别
A-Softmax与L-Softmax的最大区别在于A-Softmax的权重归一化了。A-Softmax权重的归一化导致特征上的点映射到单位超球面上,而L-Softmax则不没有这个限制,这个特性使得两者在几何的解释上是不一样的。
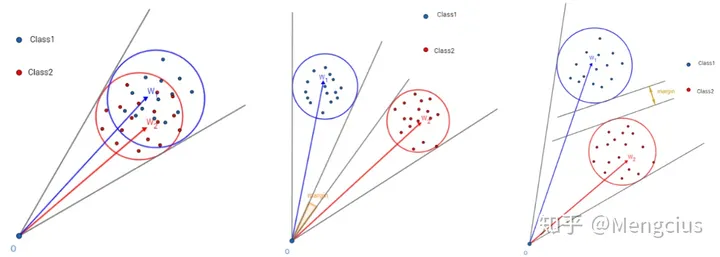
如在训练时两个类别的特征输入在同一个区域时发生了区域的重叠,如图左边。A-Softmax只能从角度上分离这两个类别,也就是说它仅从方向上去分类,分类的结果如图中间;而L-Softmax不仅可以从角度上区别两个类,还能从权重的模(长度)上区别这两个类,结果如图右边。在数据集合大小固定的条件下,L-Softmax能有两个方法分类,训练可能没有使得它在角度与长度方向都分离,导致它的精确可能不如A-Softmax。
测试结果
- 训练数据集:CASIA-WebFace,共有10575个人的494414张人脸图片。这些人脸图像水平翻转以进行数据增强。请注意,我们的训练数据(0.49m)的规模相对较小,特别是与DeepFace[30](4M)、FaceNet[22](200M)和VggFace[20](2M)中使用的其他私有数据集相比。
- 训练参数:这些模型在四个GPU上以128的批量大小进行训练。学习率从0.1开始,在16K,24K迭代中除以10。训练以28k次迭代完成。
- SphereFace特征在角空间中具有很强的可分离性,m越大,特征内聚性越强,不同类别更容易区分开,正对和负对距离越远。第一行是CASIA-WebFace里的6个类投影在单位球面上的三维特征。第二行是正对和负对的角度分布(我们从子集中选择class 1和class 2来构造正对和负对),所有的角都用弧度表示。
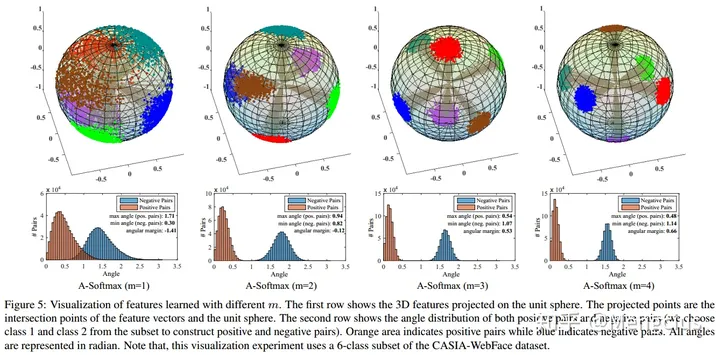
- m会影响性能:m越大,准确性越大。
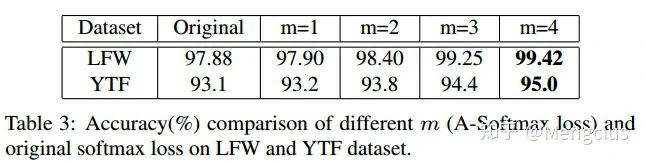
- 卷积层数影响性能:卷积层数越大性能越大,A-Softmax比Softmax性能高很多
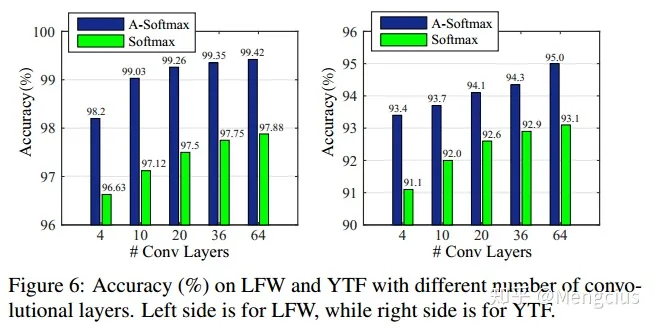
- LFW上99.42%,YTF上95.0%。不如FaceNet,和DeepID2+、DeepID3相当,但它的训练集比FaceNet的小,CASIA-WebFace有49万张图片,1万个人。SphereFace仅使用公开可用的小规模数据集实现最先进的性能, 而其它商业算法使用私有和大规模数据集
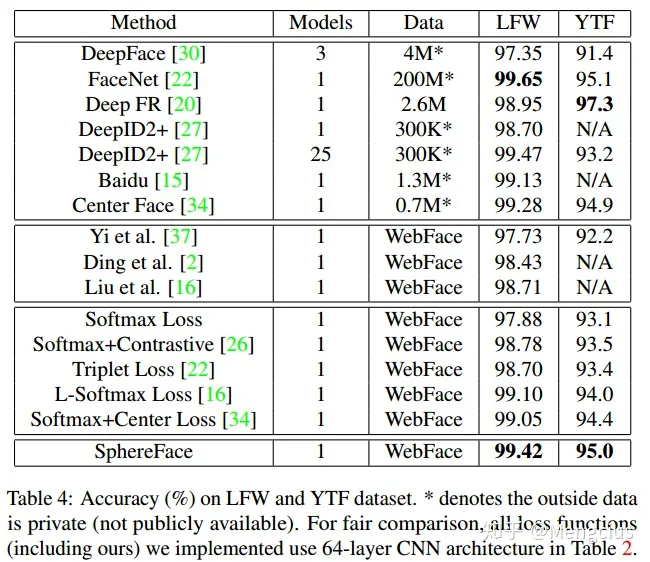
- MegaFace上Rank-1 Acc是75.766,Ver是89.142(TAR for 10^-6 FAR)。
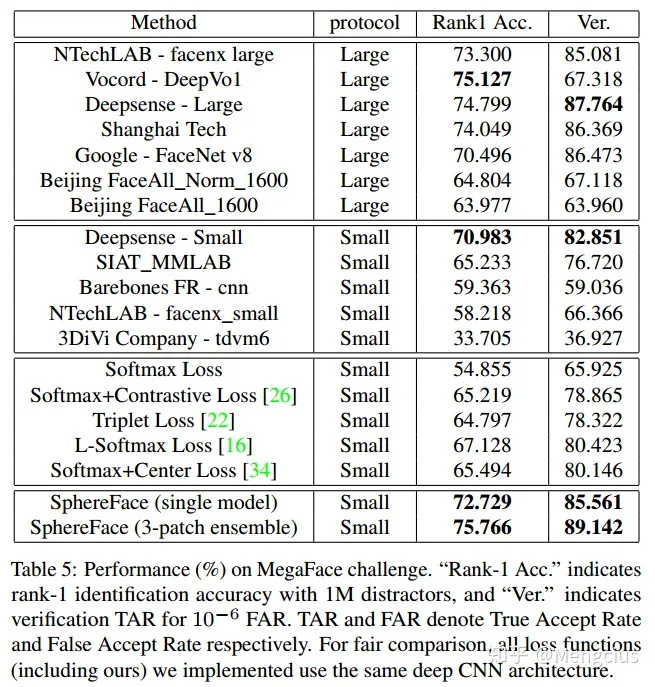
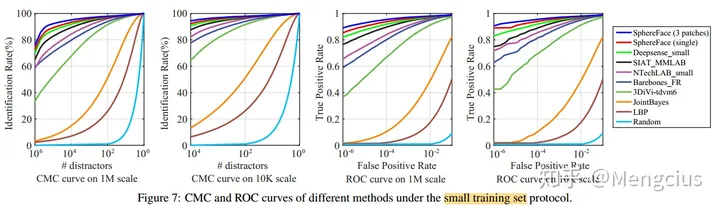
- 用小数据集训练的算法的ROC比较
附录
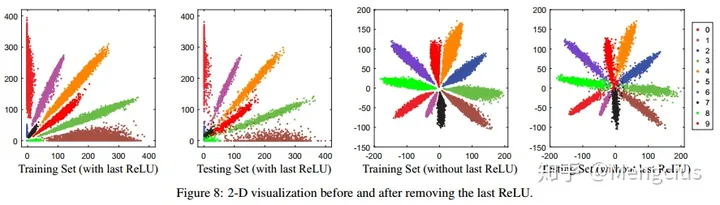
- 移除最后一个relu层:标准CNNs通常将relu连接到fc1的底部,因此所学习的特性将只分布在非负分布中,范围为[0,+∞),这限制了CNN的学习空间(角度)。为了解决这个缺点,SphereFace提出删除底部的relu非线性。直观地说,删除relu可以大大有利于特征学习,因为它提供了更大的可行学习空间(从角度度量学习角度考虑)。
- 将权重归一化可以隐式地减少训练数据不平衡问题(例如训练数据的长尾分布)带来的先验问题。
- 去除偏差:标准CNNs通常保留全连接层中的偏置项,但这些偏置项使得分析所提出的A-SoftMax loss 变得困难。这是因为SphereFace的目的是优化角度和产生角度间隔。实验得,将偏置归零对特征分布没有直接影响。有偏置和无偏置的学习特征都能充分利用学习空间。
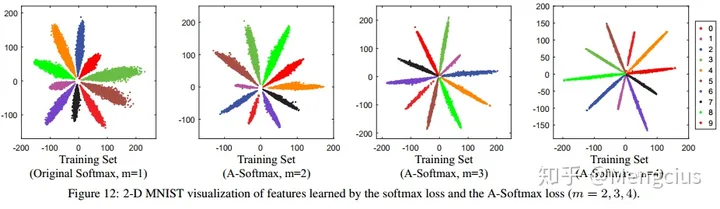
- MNIST数据集上A-Softmax loss的二维可视化:很明显,随着m的增大,学习到的特征由于较大的类间角度间隔而变得更具辨别力。
参考资料
https://zhuanlan.zhihu.com/p/76539587
https://www.cnblogs.com/heguanyou/p/7503025.html
https://blog.csdn.net/u014380165/article/details/76946380
https://blog.csdn.net/u014380165/article/details/76864572
作者源码(Matlab+caffe)
TF训练MNIST 0.9896
PyTorch训练CASIA-WebFace LFW0.9922