机器学习-KL散度与交叉熵概念辨析

KL散度

深度学习中，常用KL散度衡量两个数据分布之间的差异，KL散度越小，则表示两个数据分布之间的差异越小。一般以 P(x) 表示样本的真实分布，Q(x)作为模型预测的分布。例如，在一个三分类任务中，x1，x2，x3分别表示猫、狗和马。若一张猫的图片的真实分布P(x)=[1,0,0]，而预测分布为Q(x)=[0.7,0.2,0.1]，则对应的KL散度计算如下：

---

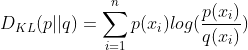
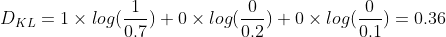
交叉熵

在介绍交叉熵之前，首先补充一下以下重要概念：

信息量

设某一事件发生的概率为P(x)，则其信息量表示为：

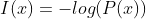
信息量是衡量一个事件发生的不确定性，大小与事件发生的概率呈反比，一个事件发生的概率越大，那么其不确定也就越小，即信息量越小。

熵

信息量的期望叫做熵。熵在化学中也是描述混乱程度(不确定性)的一个指标，在计算机领域含义依旧相似。熵的计算公式如下：

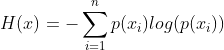
对于0-1分布，设事件发生的概率为P(x)，不发生的概率为1-P(x)，则熵的计算公式可简化为：

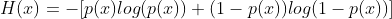
这里就引出了交叉熵的概念，交叉熵的计算公式如下：

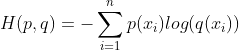
其中p(x)为真实样本的分布(或概率)，q(x)为模型输出的分布(或概率)，因为同时包含了真实数据分布信息和模型预测分布信息，故得名交叉熵。所以说了一大堆，交叉熵和KL散度到底啥关系？

简单来说：KL散度 = 交叉熵 - 信息熵(常数)

因为信息熵可以看作是个已知的常数，并且交叉熵的计算公式相对而言更简单，所以实际运用中常常用交叉熵的计算代替KL散度而实现一样的效果，即使得模型预测的分布Q(x)更接近于实际样本分布P(x)。下面请看公式推导过程(不想看公式的建议可以直接跳到代码实现部分)：

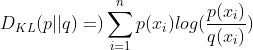
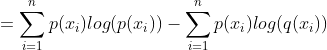
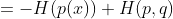
其中，H(p(x))被称为信息熵，因为真实的样本分布一般是已知的，所以p(x)可以看作是常数，故H(p(x))也为常数，因此就得出了这篇文章最核心的东西：KL散度 = 交叉熵 - 信息熵(常数)

---

代码实现

import torch
import torch.nn as nn
import numpy as np
 
loss_f = nn.CrossEntropyLoss(weight=None, size_average=True, reduce=True)
 
pred1 = torch.from_numpy(np.array([
                      [0.7, 0.2, 0.1],
                      [0.3, 0.5, 0.2],
                      [0.2, 0.2, 0.6]])
                    )
pred2 = torch.Tensor(np.array([
                      [0.2, 0.7, 0.1],
                      [0.3, 0.2, 0.5],
                      [0.6, 0.2, 0.2]])
                    )
target = torch.Tensor(np.array([0, 1, 2])).type(torch.LongTensor)
 
loss1 = loss_f(pred1, target)
loss2 = loss_f(pred2, target)
 
print("loss1:", loss1)
print("loss2:", loss2)

输出

loss1: tensor(0.8527, dtype=torch.float64)
loss2: tensor(1.2527)

值得注意的是上述代码等价于

import torch
import torch.nn as nn
import numpy as np
 
 
softmax = nn.Softmax(dim=-1)
nll_loss = nn.NLLLoss(reduce=True)
 
 
pred1 = torch.from_numpy(np.array([
                      [0.7, 0.2, 0.1],
                      [0.3, 0.5, 0.2],
                      [0.2, 0.2, 0.6]])
                    )
pred2 = torch.Tensor(np.array([
                      [0.2, 0.7, 0.1],
                      [0.3, 0.2, 0.5],
                      [0.6, 0.2, 0.2]])
                    )
target = torch.Tensor(np.array([0, 1, 2])).type(torch.LongTensor)
 
loss1 = nll_loss(torch.log(softmax(pred1)),target)
loss2 = nll_loss(torch.log(softmax(pred2)),target)
 
print("loss1:", loss1)
print("loss2:", loss2)

输出：

loss1: tensor(0.8527, dtype=torch.float64)
loss2: tensor(1.2527)

可以看出效果是一样的，这是因为在pytorch的代码实现中，交叉熵的计算公式为：

也就是先计算Softmax

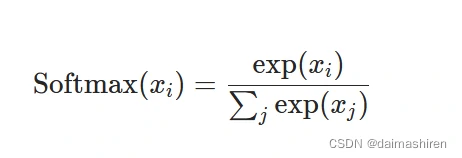
在Softmax的输出结果上取Log值之后再计算NLLLoss(直接取target（下面公式中为y）对应的模型的输出再加个负号)

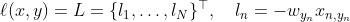
例如上述代码实现中，target=[0, 1, 2]分别表示预测的正确类别分别是0,1,2，对应到模型的输出pred1中就是0.7,0.5和0.6。对应的NLLLoss就分别是-0.7,-0.5和-0.6。因此，在pytorch的代码实现中 CrossEntropy 的作用效果等价于 Softmax 与 Log 以及 NLLLoss 作用的叠加。

注意：CrossEntropy公式中使用Softmax和Log就相当于是把原本模型直接输出的预测值变成了取了log之后的概率值，而NLLLoss的作用就是把对应于正确标签的那个概率值选出来再添个负号从而去Minimize这个值(也就是最大化这个概率值)

---

参考资料

CrossEntropyLoss — PyTorch 1.10.1 documentation
Softmax — PyTorch 1.10.1 documentation
torch.nn.modules.loss — PyTorch 1.10.1 documentation
KL散度与交叉熵概念辨析