- CS231n - Convolutional Neural Networks
卷积神经网络历史-略过
具体参照Lecture5已经总结
CNN适用于分类、恢复、探测、分割,随着GPU的兴起和互联网数据的增大,CNN现在是无处不在。以风格迁移为例。

卷积神经网络层
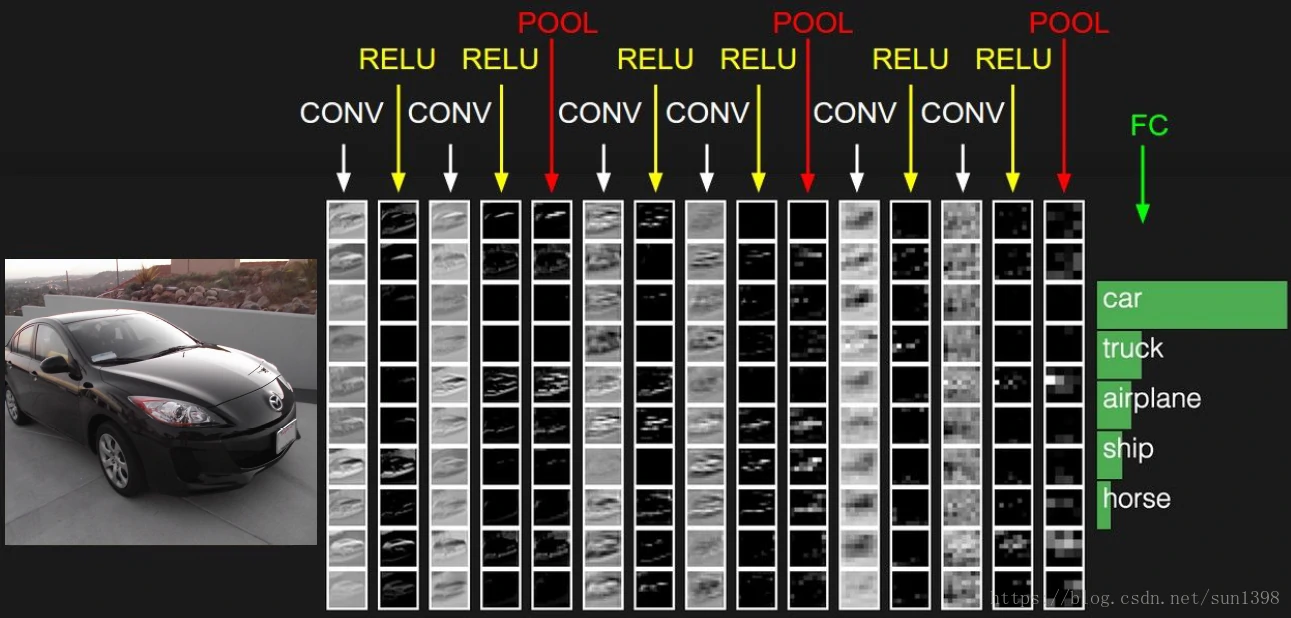
- 典型的神经网络构成:卷积层+池化层+全连接层
卷积层
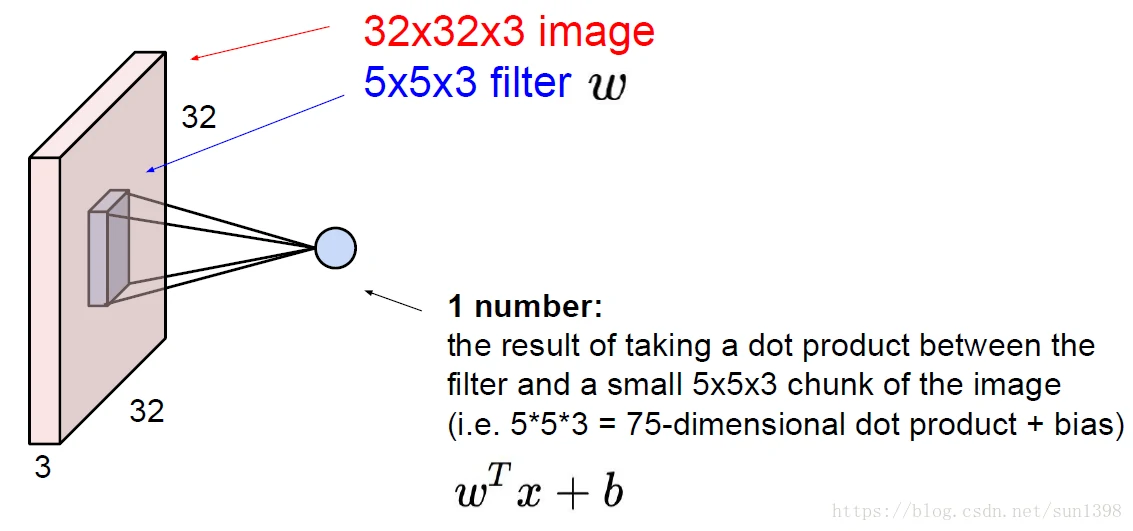
三维卷积与一维、二维的卷积意义是一样的,都是滤波器的作用,传统的都是需要人为设置各种特征提取的滤波器,而CNN的滤波器是可以训练出不同功能的,全面而又强大
这个地方关于滤波的内容吴恩达的深度学习课程中讲解的更为透彻。
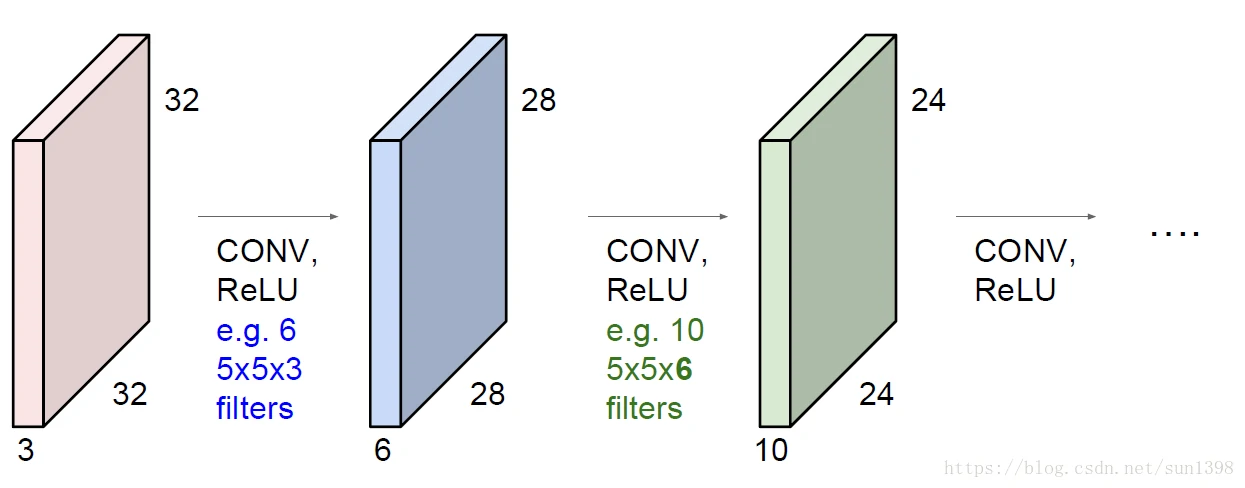
- 经过两层卷积层后的数据结构变化,维度从3232–2828–24*24,宽和高是在缩小,深维度由每层滤波器个数决定。
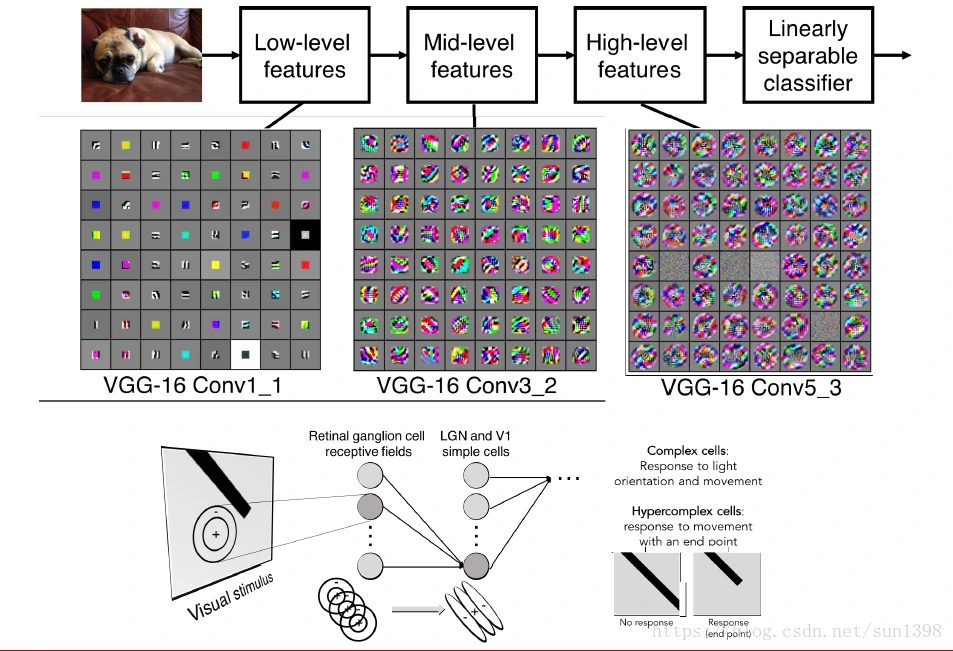
- 卷积神经网络不同层提取的特征不一样,越靠前的网络提取的特征越简单,越往后越复杂,可以通过可视化的展现来观察不同层的功能。
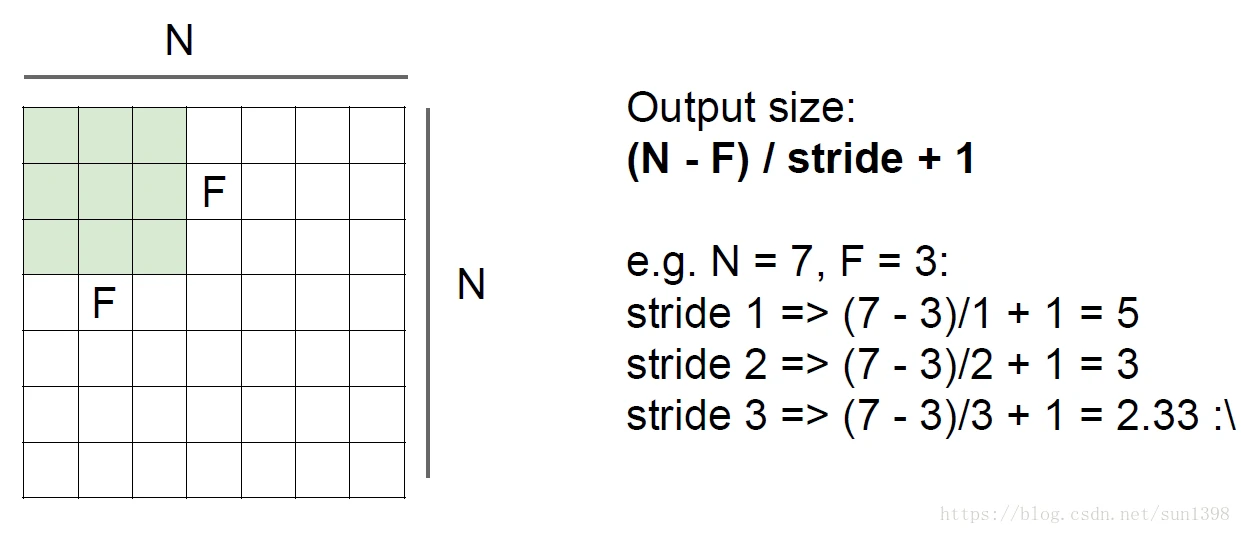
- 经过卷积层后,数据维度变化规律,必须满足输出是整数才能运行,除不尽的情况不合理。

- 实际上如果我们的层数比较多,100层,经过这样的维度下降后,宽和高无法维系,因此需要使用zero padding来保持维度不变。

- 实际上对于卷积层,参数包括;滤波器数量K、滤波器大小F、步长S和填充padding;实际上可以用偶数滤波器,但不常见,因为偶数没有中间,通常3是最常见的最小滤波器大小。
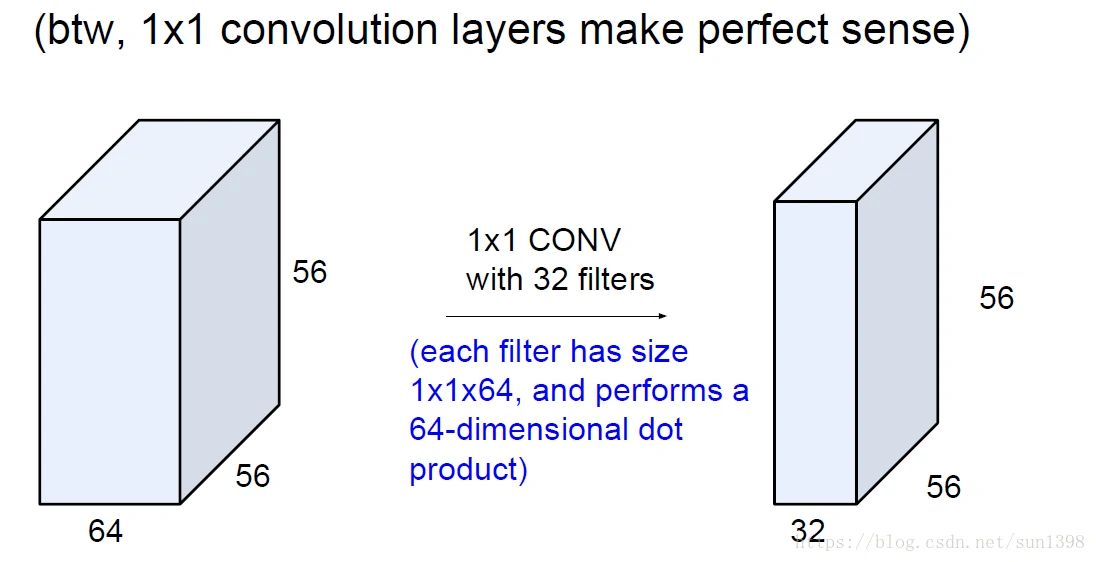
- 1维滤波器经常有特殊用法,用于对不同深度进行成比例混合压缩,重建新的深度维度,而维持长宽不变。
卷积层与人脑的解释
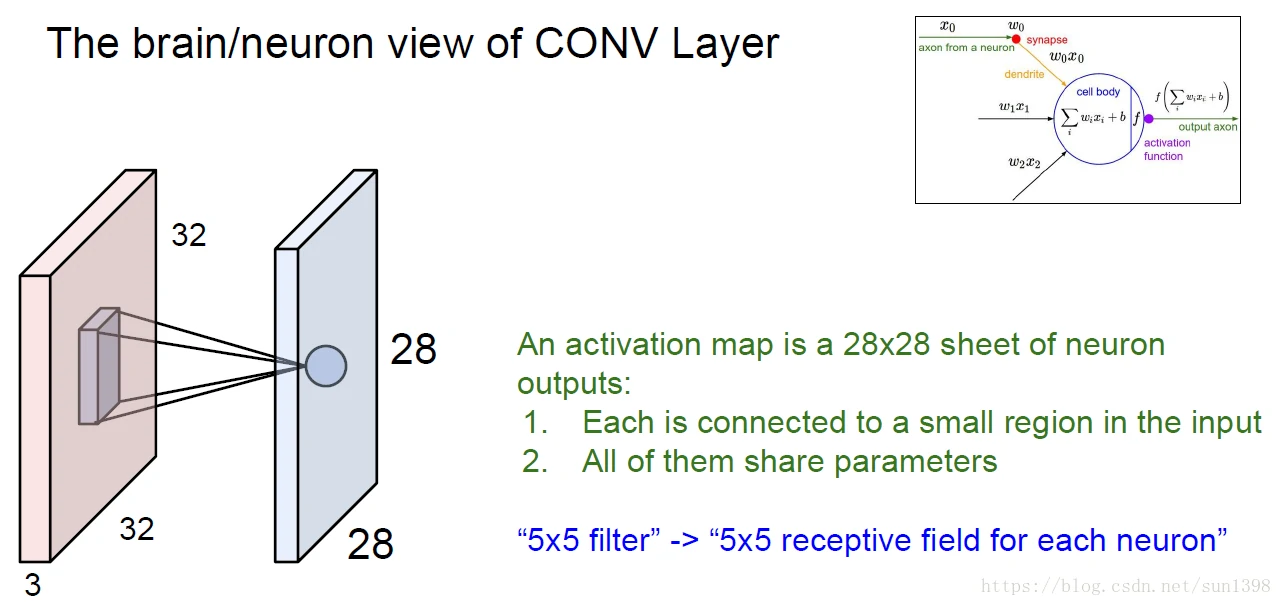
池化层
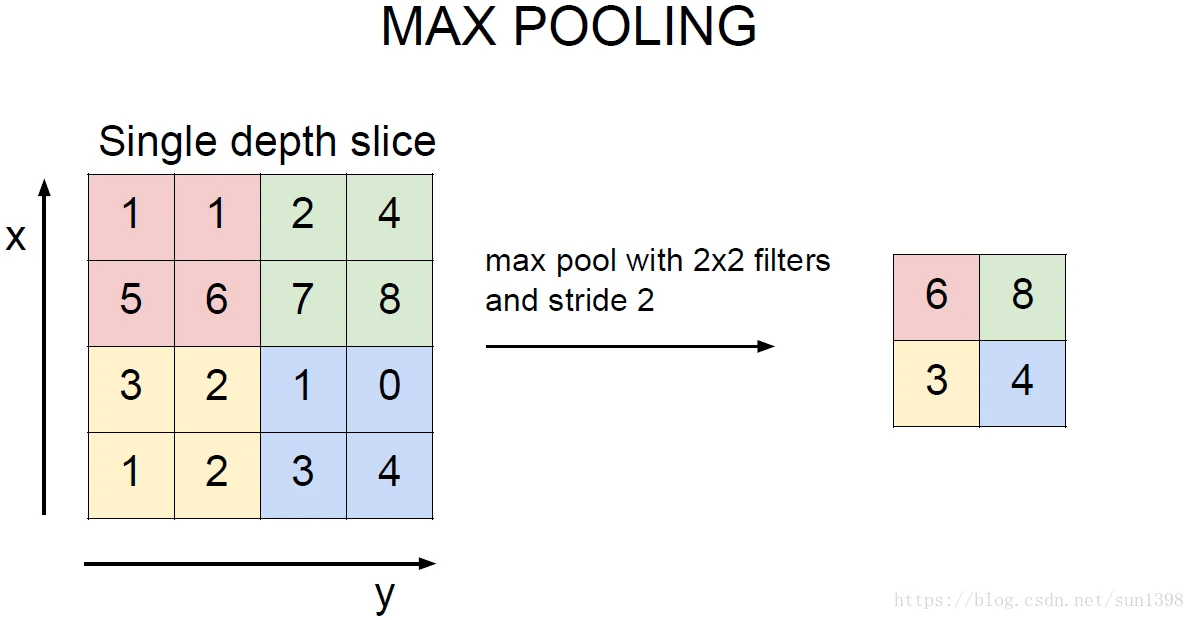
在卷积层尽量保持维度的不变行,但是滤波器数量大的时候,需要经过池化层对数据维度进行降低,与卷积层相同,通常关注池化滤波器大小K以及步长S。
池化包括最大层池化、均值池化等。
全连接层
- 全连接层与之前的神经网络层相同就是用来最后进行分类的层。
神经网络Cases
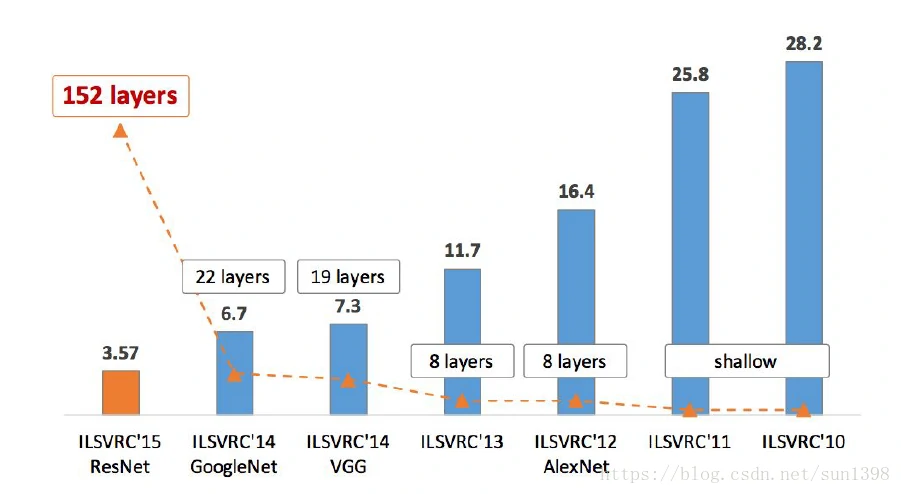
- 图片识别错误率下降过程
LeNet-5–1998
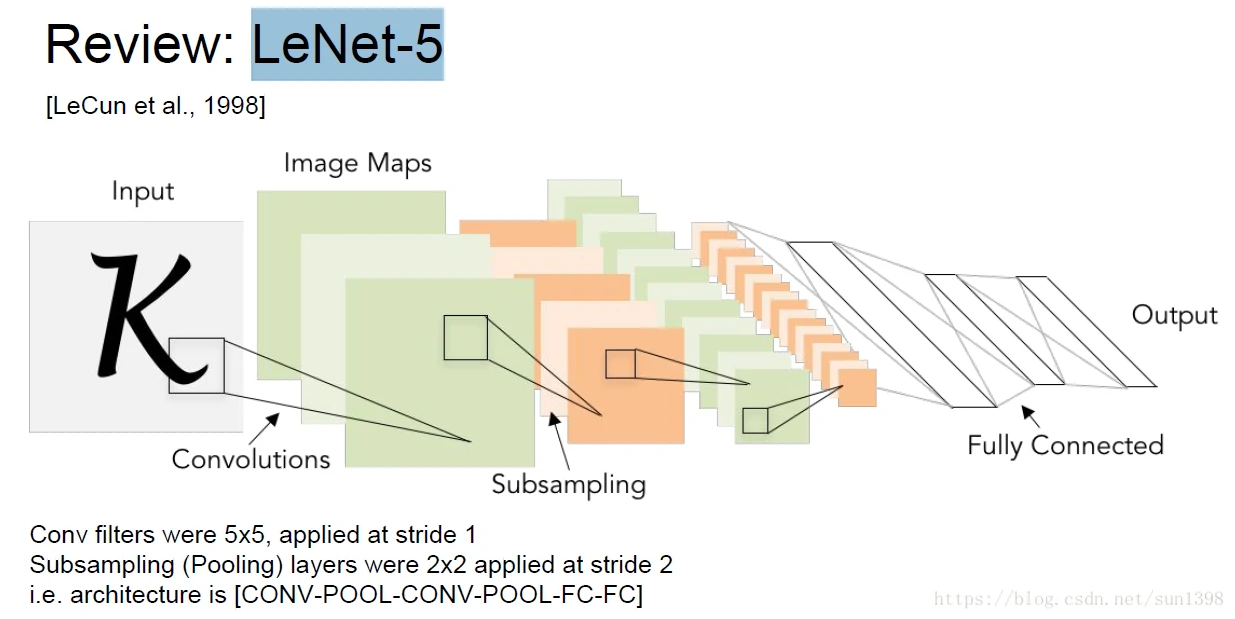
AlexNet–2012

ZFNet–2013
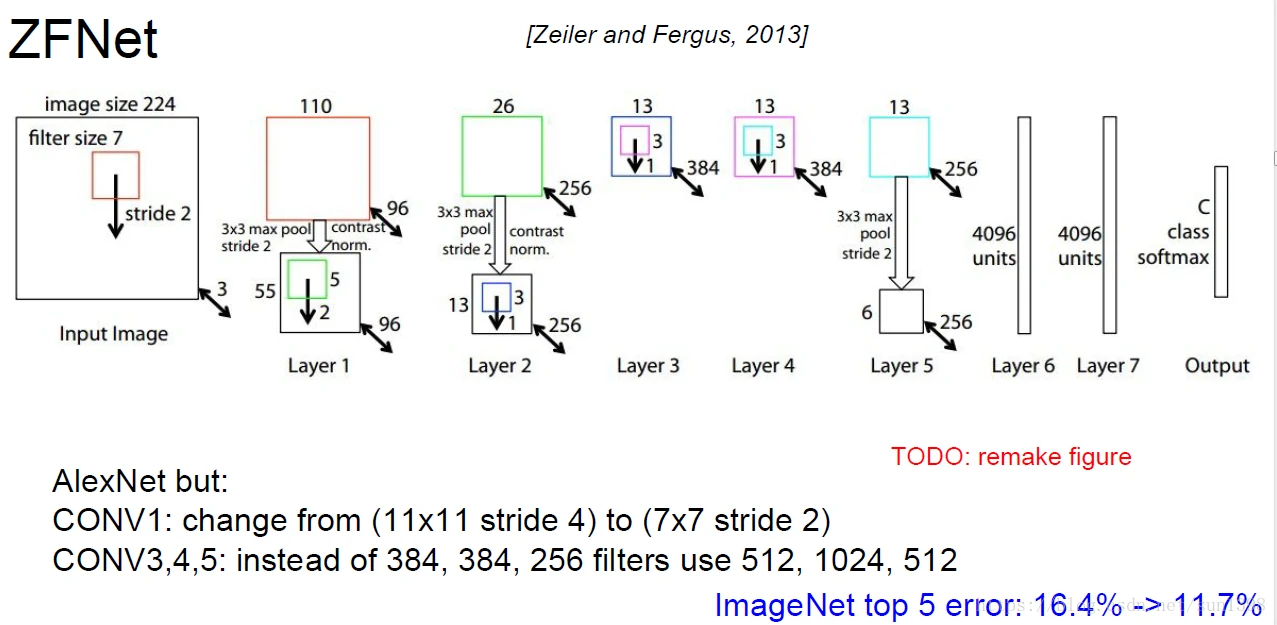
VGGNet–2014


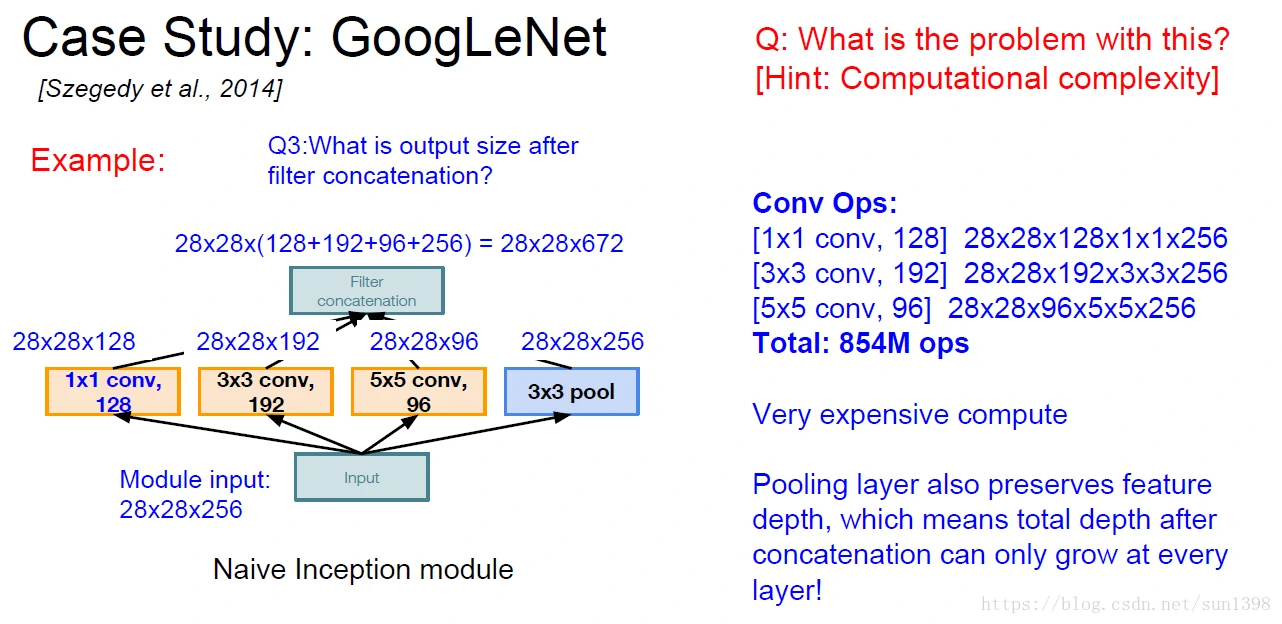
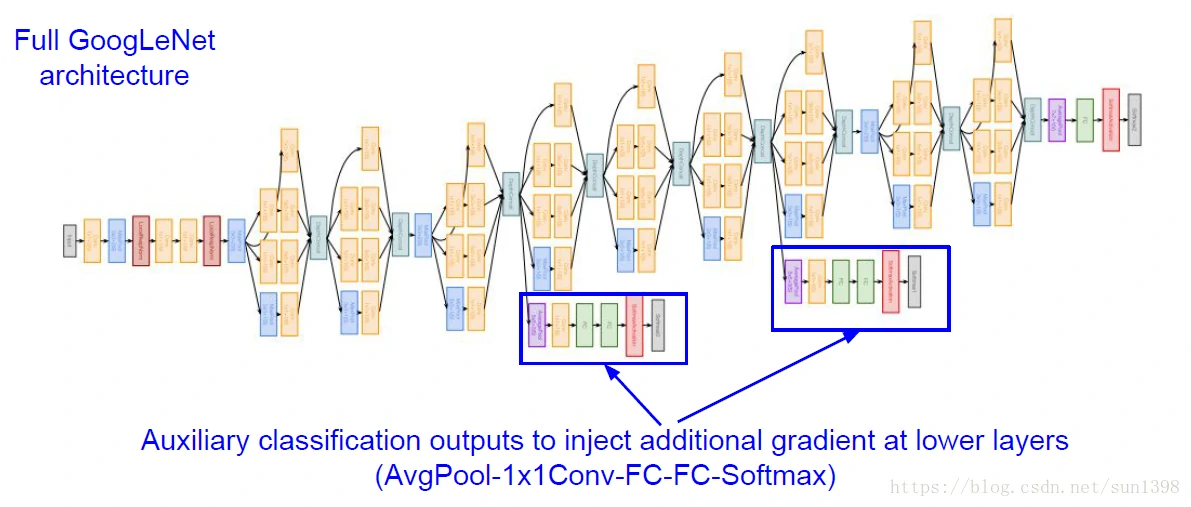
GoogLeNet–2014
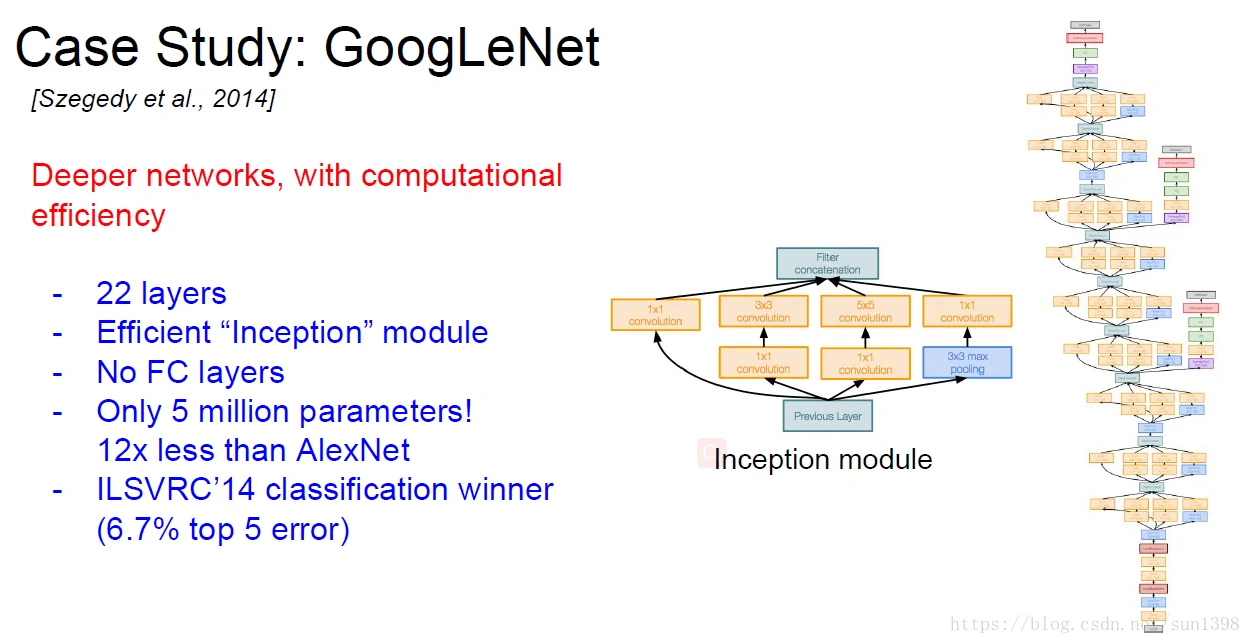
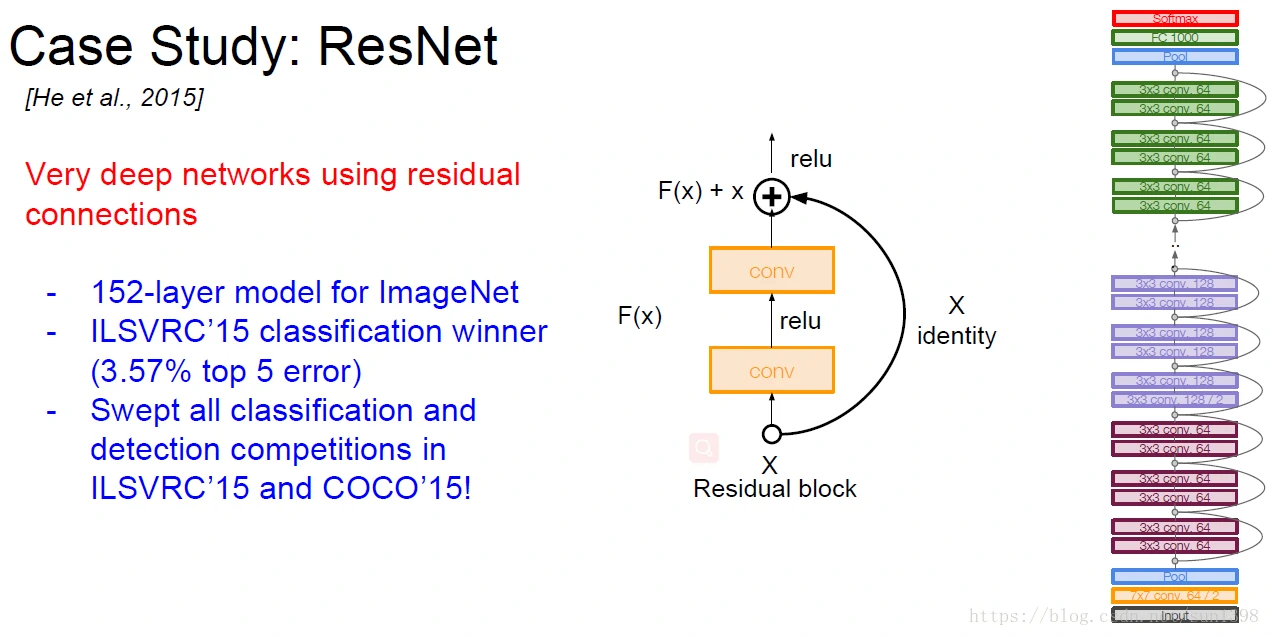
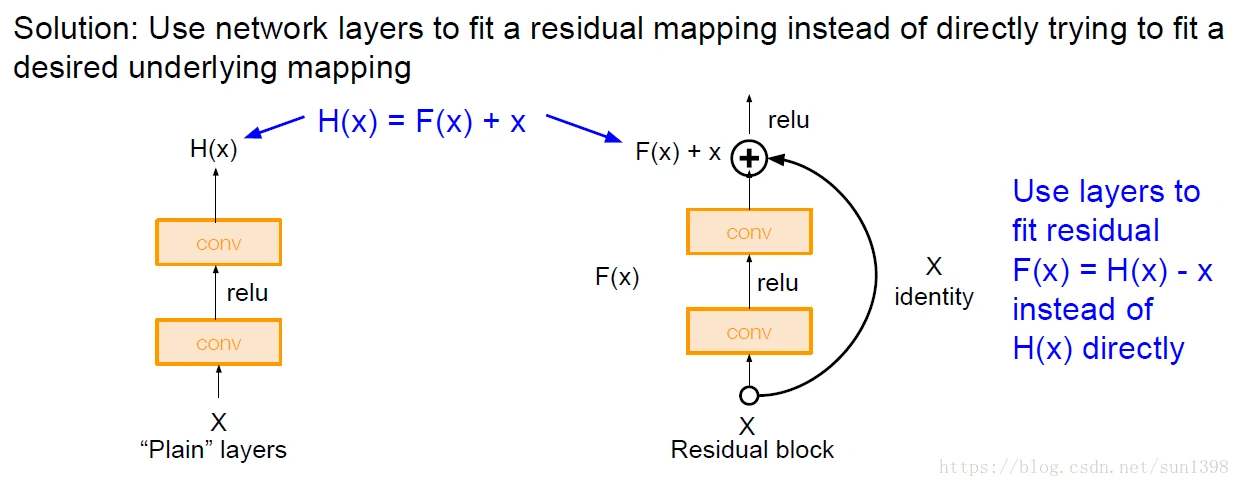
ResNet–2015

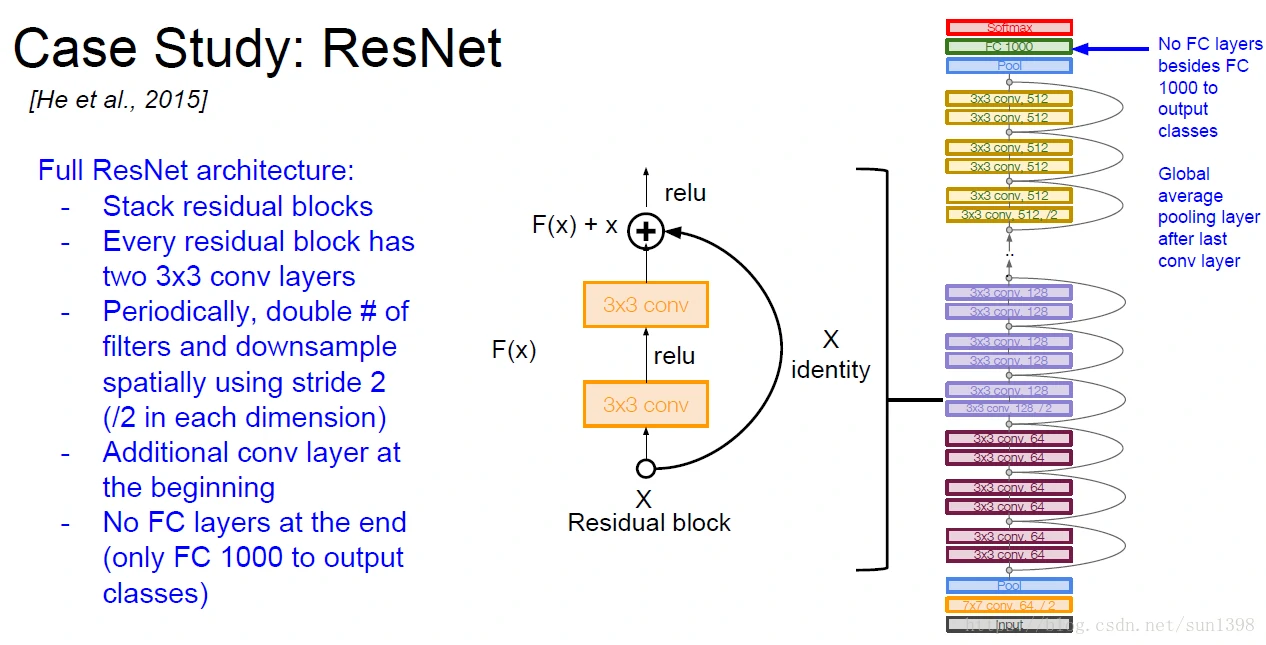
计算、时间复杂度、能量复杂度
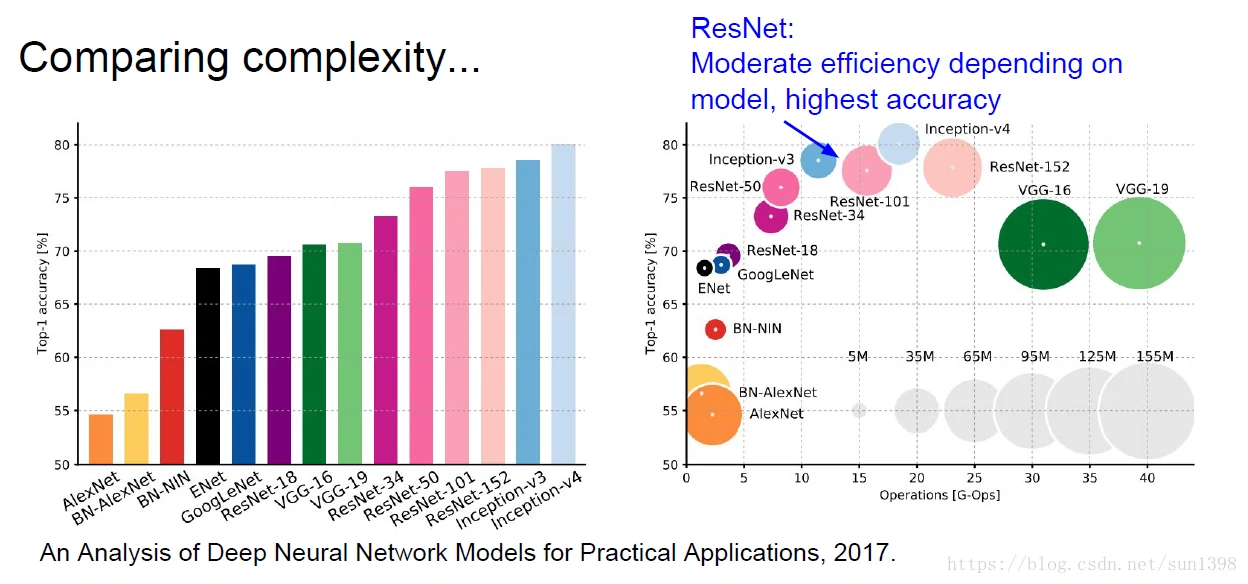
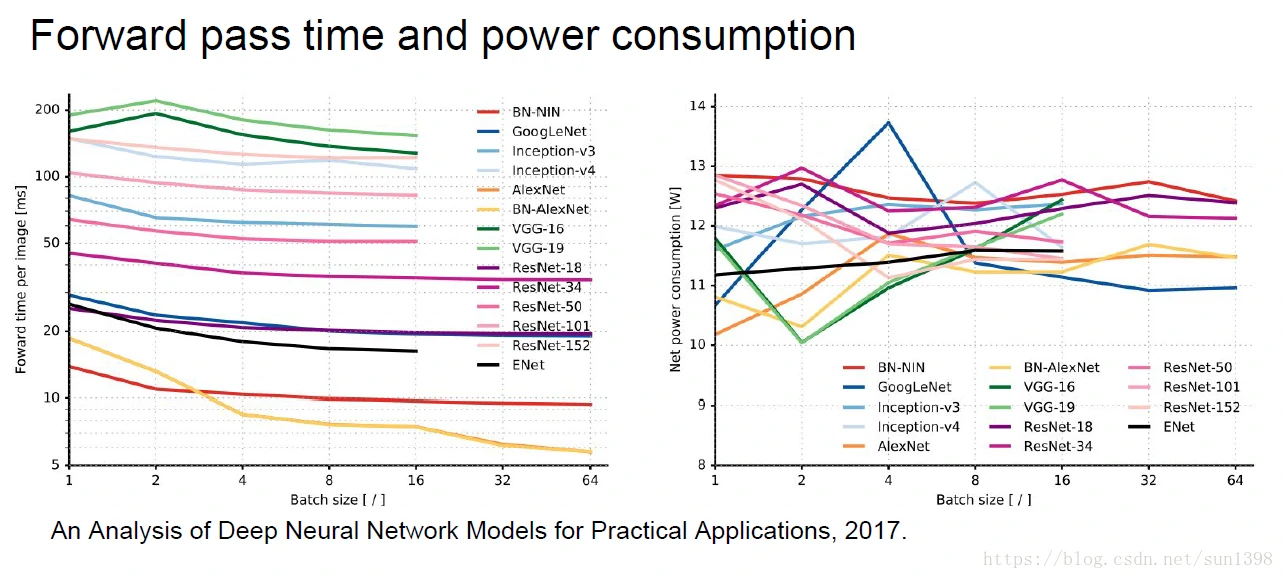
其他结构–雨后春笋般冒出来
- Network in Network (NiN)–2014
- Identity Mappings in Deep Residual Networks–2016
- Wide Residual Networks–2016
- Aggregated Residual Transformations for Deep Neural Networks (ResNeXt)–2016
- Deep Networks with Stochastic Depth–2016
- FractalNet: Ultra-Deep Neural Networks without Residuals–2017
- Densely Connected Convolutional Networks–2017
- SqueezeNet: AlexNet-level Accuracy With 50x Fewer Parameters and <0.5Mb Model Size–2017