- CS231n - Training Neural Networks II
精细优化
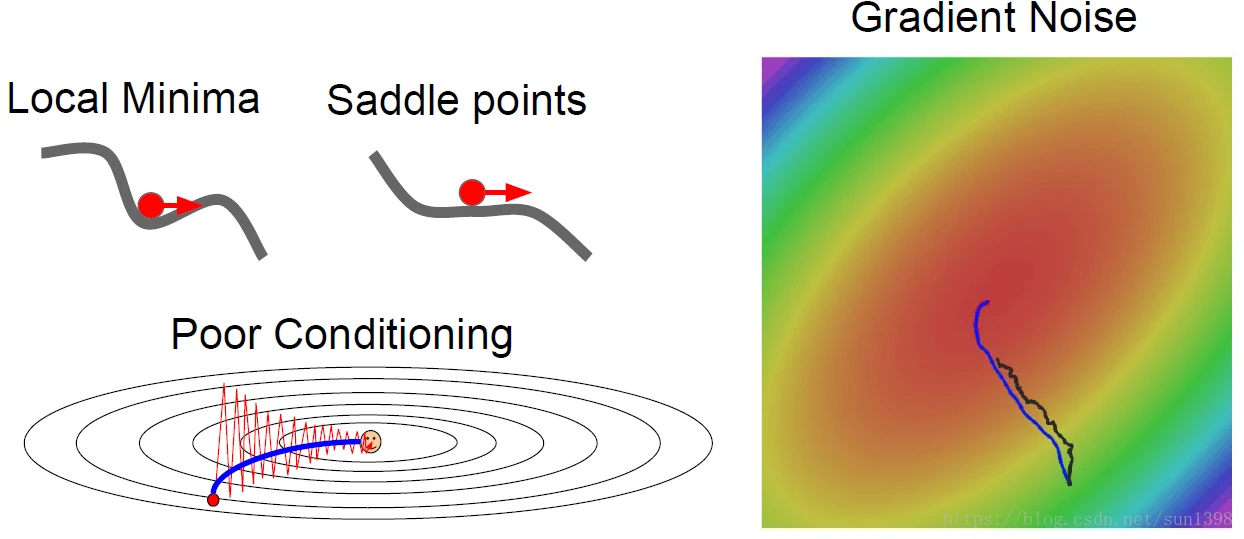
SGD的优化问题
不同维度梯度问题
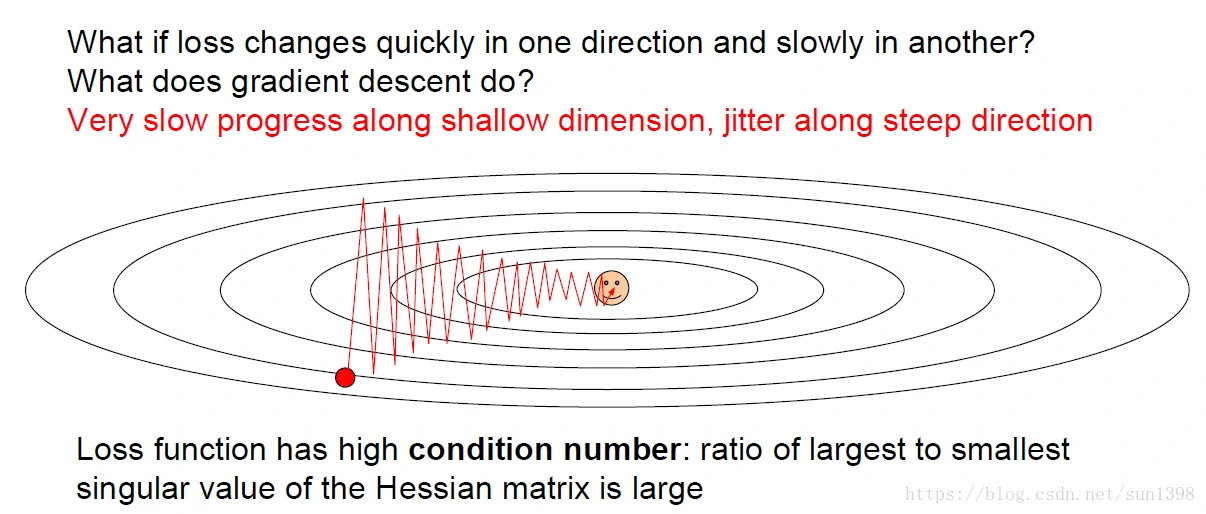
- 比如在趋近最优解的维度,梯度下降的慢,而在垂直方式梯度下降的快,梯度下降的和方向在偏离正确方向太远,这样优化过程中逼近最优解速度慢,这也是SGD速度最慢的原因
极值点问题
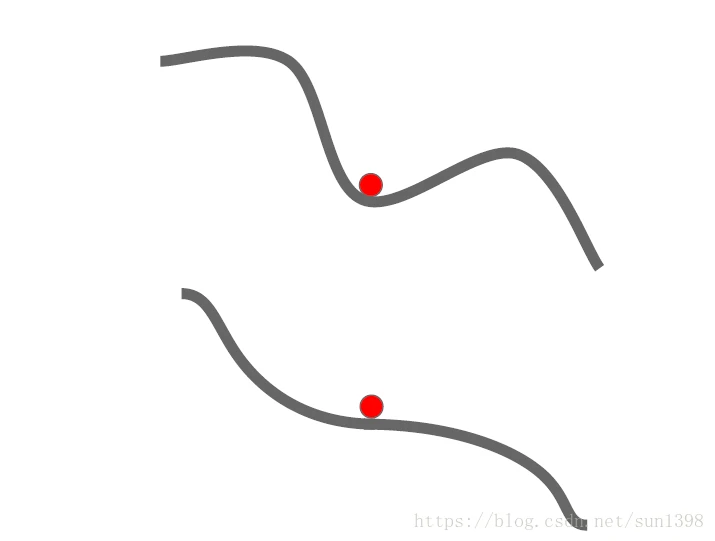
- 当遇到局部最小值点及鞍点时,SGD会陷入局部最优;由于数据维度较大,很难存在局部最小值点的情况,鞍点的存在可能性更大
- 个人认为SGD是在每个小批量上进行优化训练,那么实际上损失函数和梯度时存在波动性,这要局部最小值和鞍点不是很严重的话,应该是可以跳出的。
噪声问题
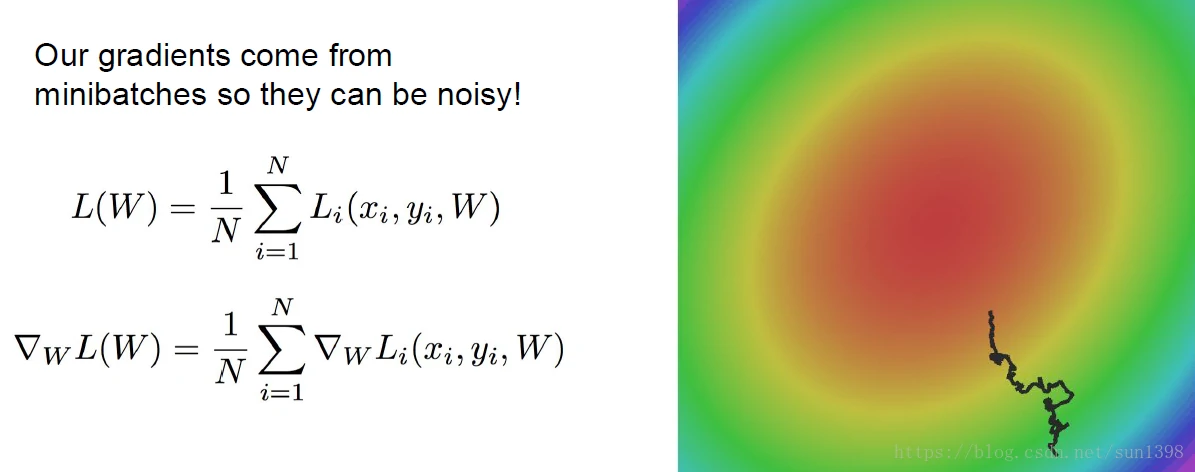
- 由于SGD是在小批量上进行测试的,那么实际上优化过程会有很多波动性,这样就会导致优化逼近存在很大噪声。
SGD + Momentum

- 引入速度V的概念,将以前的梯度考虑进去,给当前梯度更新增加一定的动量,就是梯度实际下降比当前计算的值大,这样即使在鞍点和局部最优点位置也会由于额外引入的动量冲过去,当然如果极致和鞍点区域很大,那么将会导致实际上无法冲过,这样需要增大动量的影响。
- 实际上如果考虑系数0.1以下时之前的梯度不会再产生影响,那么0.9^22=0.098,0.99^229=0.099,这样实际上动量的影响会不会比较大,实际上在后期时动量的影响增大,可能无法趋近与最佳值,但实际上后期的梯度都很小,一般不会出现这样问题。
- 实际上从信号处理的角度来讲,相当于给梯度更新增加了一个滑动滤波器,前面的梯度会被一次次以不同的系数划过,这也是能够降低噪声的原因。实际上可以设计一个模板,只取若干梯度及衰减进行更新,但实际上也没有太大意义。
- 很明显SGD + Momentum的更新方法,速度更快,噪声更小,但是在后期可能存在波动。
Nesterov Momentum(NAG)

- 与传统的Momentum的区别在于,以骑自行陈为例,M相当于在冲量的加速下骑到一个地方,然后根据当前坡度,决定车往哪走。但是NAG相当于在冲量的加速下,先用眼镜看一下前方的位置的坡度,再决定车往哪走,也就是或NAG有预判修正的作用,避免走冤枉路。因此优化过程梯度下降较为平滑
- NAG在凸优化问题中,尤其是对平滑度较高的函数有很好的效果,但实际深度学习中由于数据的复杂性,还是需要看实际结果进行参数调整。
- 变换的目的,是不需要在去算一个预判的梯度,而使用当前参数的梯度进行计算,是一种近似。
AdaGrad

- 这个算法字面的意思就是Adaptive Gradient,自适应学习率,初始使用一个较大的学习率,后期在逼近最优值的过程不断减小学习率。
- AdaGrad非常适合样本稀疏的问题,稀疏意味着样本间相似性小,样本稀疏,每次梯度下降的方向以及涉及的变量都可能有很大的差异,这样自适应学习就非常实用。
- 该算法的缺点是初始的全局学习率需要手工指定,全局学习率过大,优化同样不稳定;学习率过低,在学习过程中学习率不断下降,没到极值可能就停止了。
RMSProp
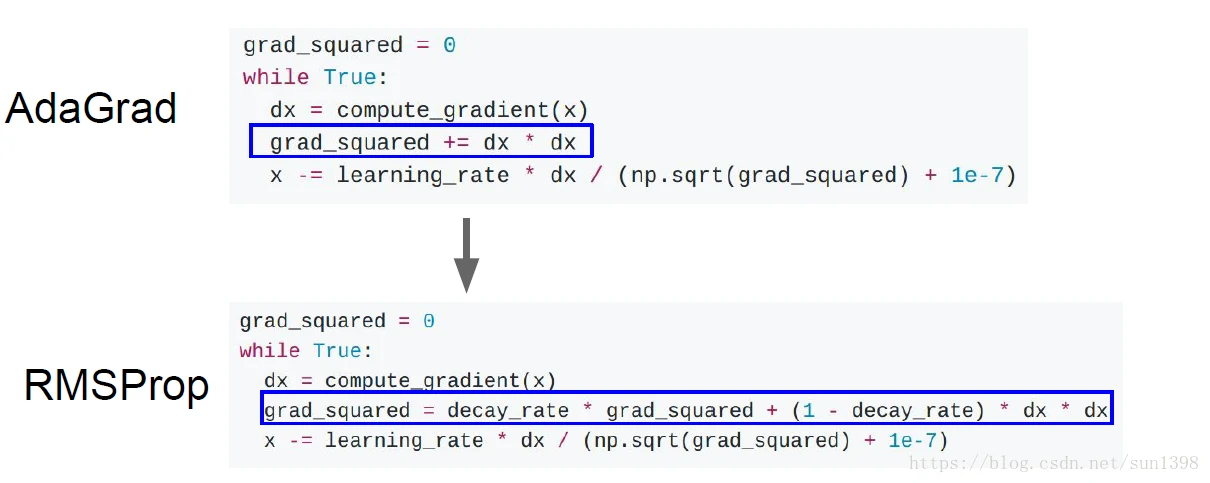
- 该算法的改进在于将累计梯度信息从全部历史梯度变为当前时间向前的一个窗口期内的积累,有些类似Momentum的速度的累加,这样解决AdaGrad持续下降的问题
- 实际上类似的还有AdaDelta,该算法还解决了手动设置学习率的问题,不需要手动设置学习率。
Adam
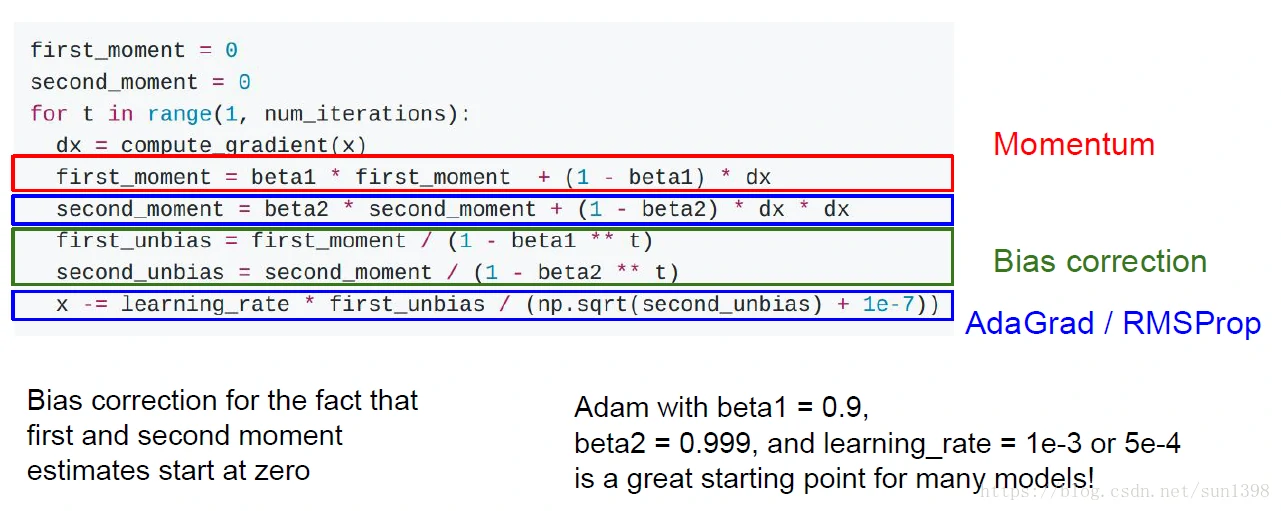
该算法将Momentum与AdaGrad/RMSProp结合起来,结合两者的优点。
学习率衰减
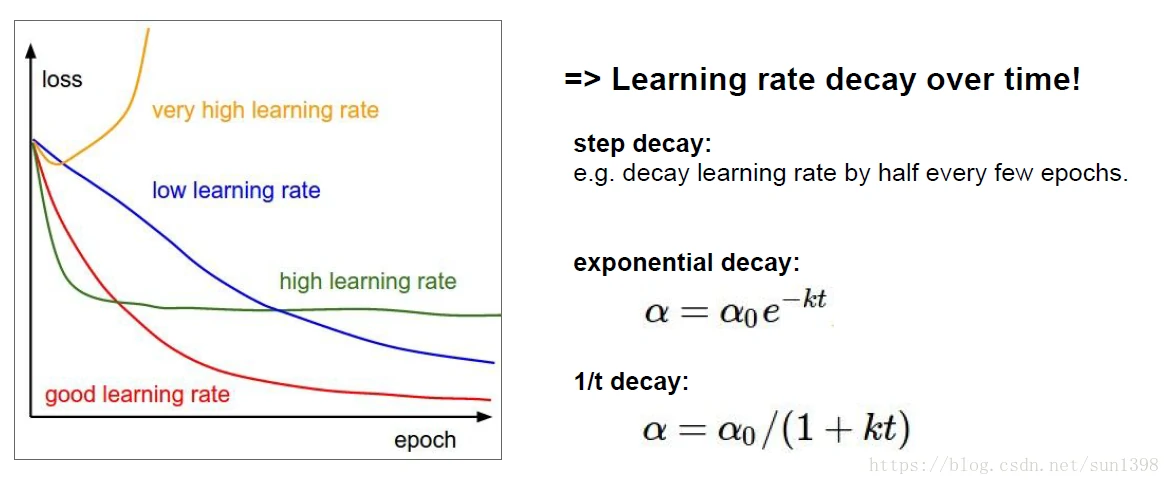
- 包括步进下降法;指数衰减法;1/t衰减法
- 实际上学习率的衰减更适用于Momentum等算法,毕竟Ada类算法都是自带学习率下降的。
二阶优化-LBFGS
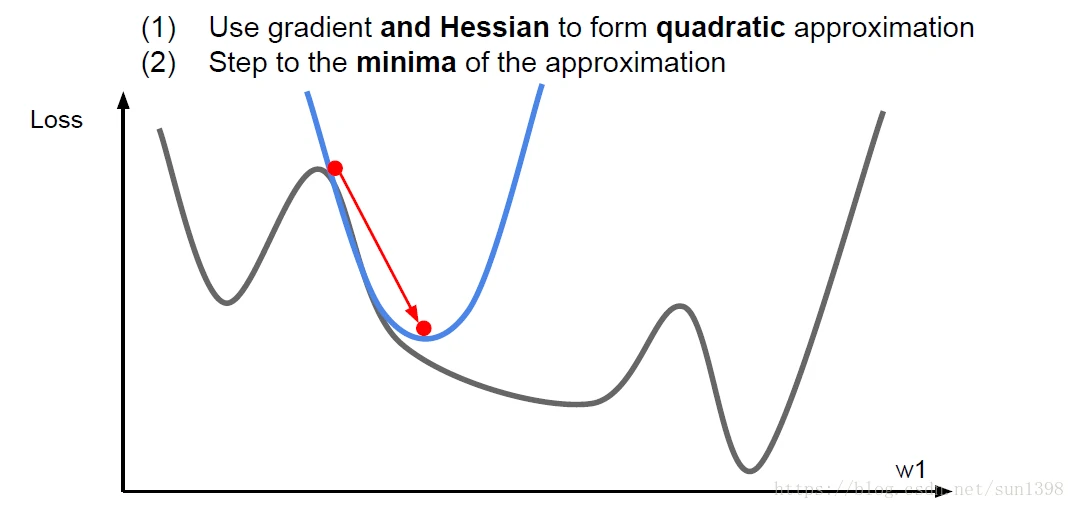
- 利用泰勒二阶展开和牛顿参数来进行参数权重更新,优点是没有超参数,没有学习率,但缺点是用到Hessian矩阵(二阶偏导矩阵)计算量复杂
- 牛顿近似法(BFGS)–参照《深度学习与计算机视觉》一书P75-P77,讲解很细致。
- L-BFGS (Limited memory BFGS):不在存储整个海森矩阵的转置,只存储部分需要使用的。
- LBFGS通常在全批量数据,f(x)确定性模式下工作得很好;不要在分割训练集mini-batch上使用它,要在大尺寸随- 机性强训练集上使用。
小结
- 在深度学习中的实际应用中,因为问题的高维度和高复杂性的特点,具体使用哪种算法那还是需要具体的尝试,一般情况下带冲量的梯度下降还是主流,但是对于收敛不好的情况下,可能使用自适应算法往往会有意想不到的效果。不过一般的情况是在优化的后期,自适应算法尤其是AdaDelta和RMSProp往往会反复震荡,反而不如带冲量的梯度下降法。
集成模型与正则化
集成模型
训练多个独立的模型;在测试时取结果的平均值——往往从统计的观点能有2%的额外优化
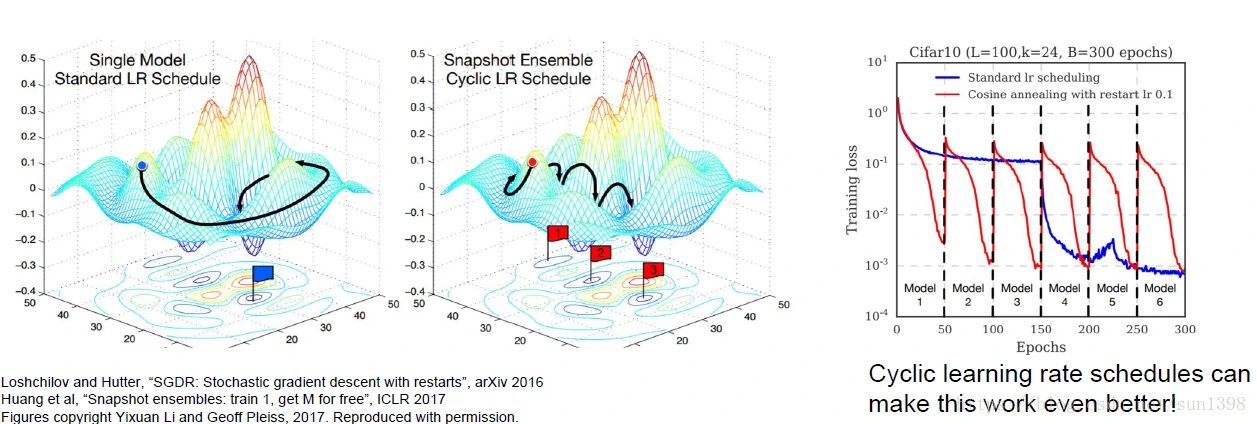
技巧1:可以使用循环的学习率来优化模型,如下图所示:
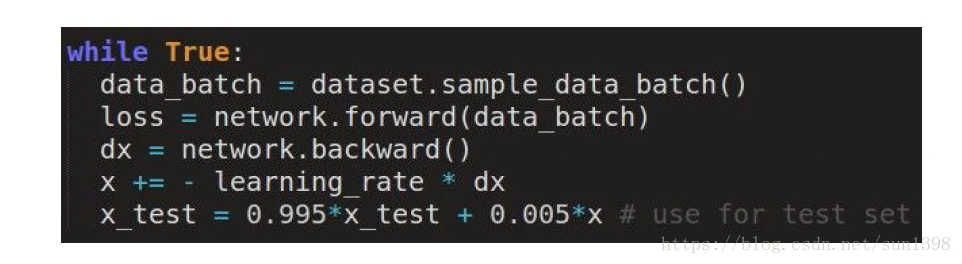
- 技巧2:对训练的权重进行滑动平均,这样在最后波动位置平均值可能更接近最优值
L2和L1正则化
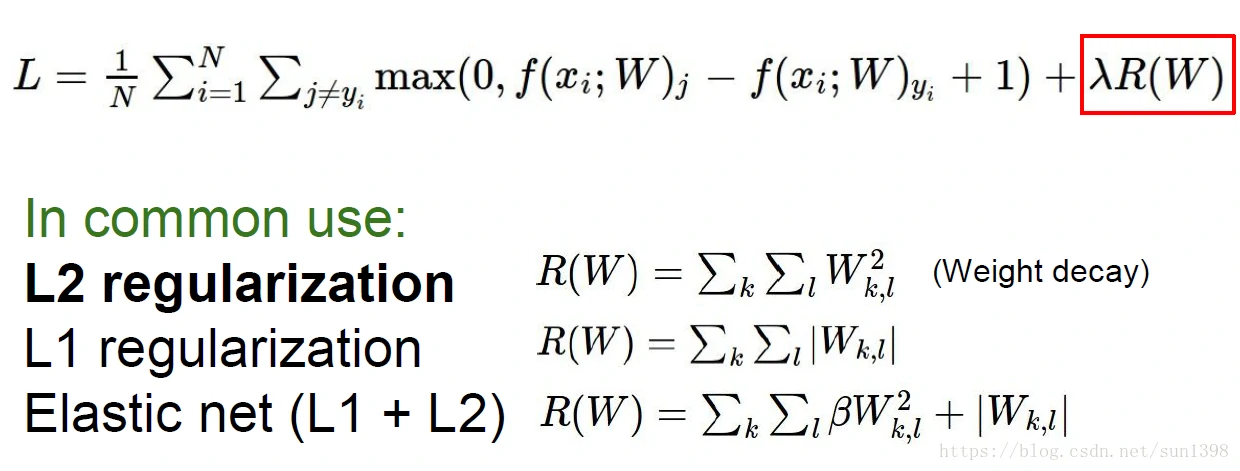
- 之前用过的L1、L2正则化,以及集成正则化
Dropout原理

- Dropout通过设定一定的概率来在每一层失活一定的神经元,这样的好处在于能够使得神经网络变得稀疏,从而减少过拟合现象,提高准确率。
- Dropout的实现是通过一个掩模矩阵与激活函数结果矩阵相乘,求梯度时采用相同的步骤乘以转置即可。
- 解释1:丢掉神经元降低网络的冗余性,同时单次训练中,随机地丢弃神经元,减少提取的特征的互相适应性,保证网络的简洁。
- 解释2:神经网络是一个大的网络,大网络是由不同小网络构成,但是小网络间参数并不能很好的训练,经过随机失活一部分网络后,在失活的神经元输出为0,反向传播经过其及以后的网络也为0,意味着每次训练都是随机地对一个小网络进行参数更新,但是最后这些小网络构成的大网络具备了随机性。
- 当然也有算法使用固定失活某些神经网络
Dropout的Test time

- 训练时随机失活一部分网络,但是测试时是一个完整的网络,这样最后的测试输出值偏大,需要进行乘以概率p修正。
- 当然更常见的做法是在掩模矩阵位置除以整个概率p,也可以修正。
- 当然实际上期望值与随机失活值是略有不同的,乘以概率p其实会有一些误差,但由于神经元数据大随机性,这点误差可以忽略。
- 增加网络训练随机性的一般的形式

梯度检查–确保模型计算的准确性
数据增加-Augmentation
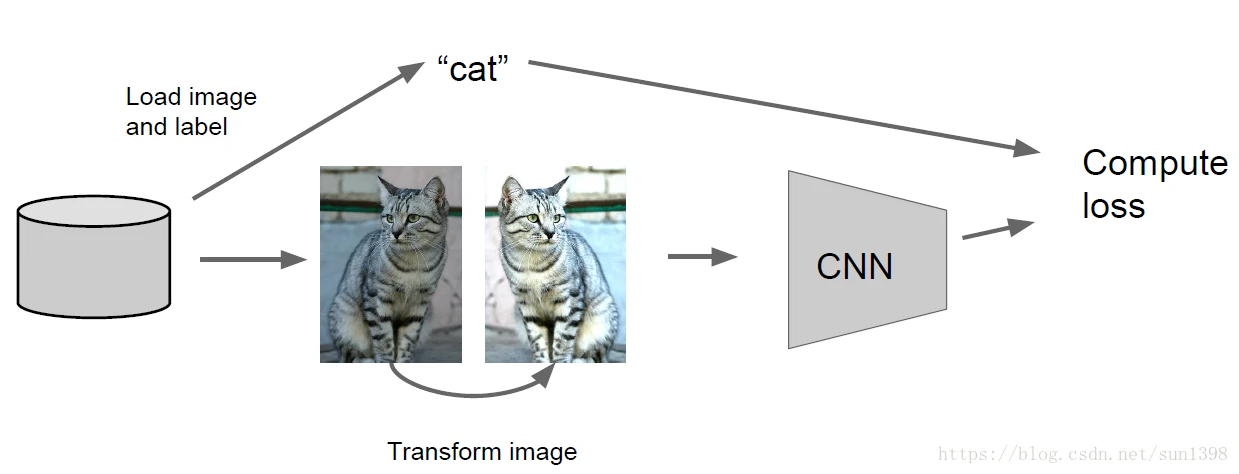
- 通过对一张图片进行一系列的操作从而增加样本数据量,增加样本多样性,减少标定时间,节约成本。
- 图像水平翻转,简单而又有效地样本数据增加。
- 残差网络,训练:随机剪裁、压缩尺度、固定大小随机剪裁;测试:按照5个尺度压缩图片,每个尺度进行4个角+中心,水平翻转。
- 颜色调整,简单:调整对比度、亮暗、饱和度;复杂,在RGB进行PCA算法、添加颜色偏移在主成分方向、添加颜色偏移到整幅图像。
- 发挥想象力,还可以有更多方法:扭曲、变形、拉伸、位移、旋转、剪裁、光学畸变等等。
其他方法
- BN;DropConnect;Fractional Max Pooling - 部分池化;随机网络深度
迁移学习
CNN上的迁移

CNN迁移例子
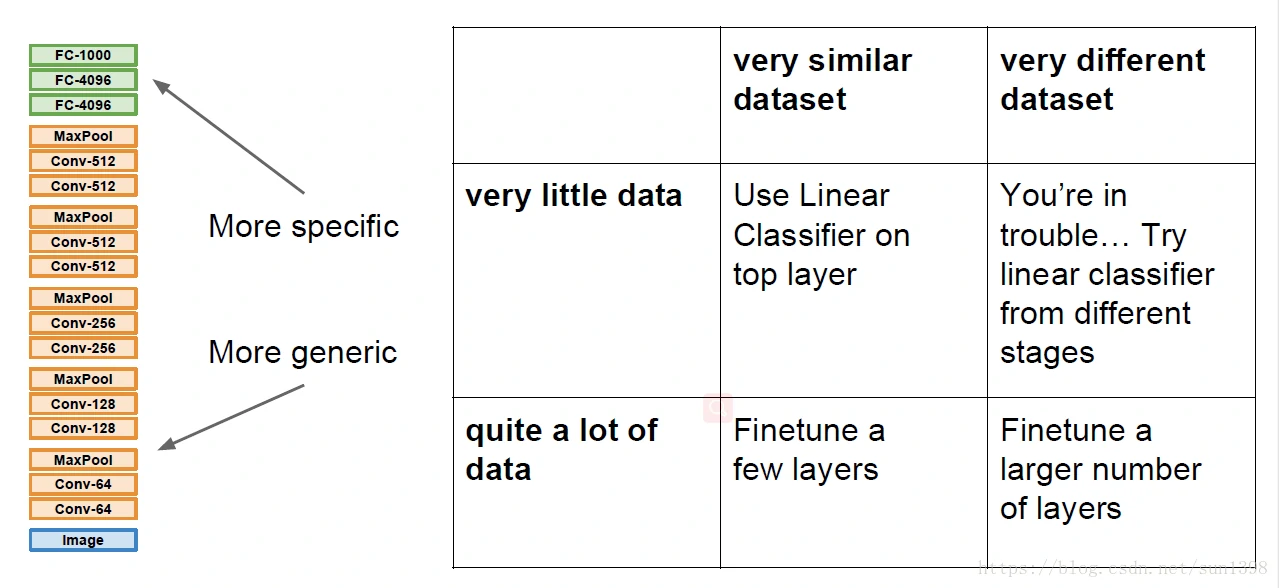
数据驱动、模型使用
