这篇文章介绍变分自编码机(Variational AutoEncoder, VAE),VAE作为可以和GAN比肩的生成模型,融合了贝叶斯方法和深度学习的优势,拥有优雅的数学基础和简单易懂的架构以及令人满意的性能,其能提取disentangled latent variable的特性也使得它比一般的生成模型具有更广泛的意义。这次会深入VAE的数学原理和实现方法,让大家对VAE有更详细的了解。
这篇文章的大部分内容都来自Tutorial on Variational AutoEncoder,有兴趣的同学可以直接看英文原版。
Latent Variable Model
生成模型一般会生成多个种类的数据,比如说在手写数字生成中,我们总共有10个类别的数字要生成,这个时候latent variable model就是一个很好的选择。
为什么呢?举例来说,我们很容易能注意到相同类别的数据在不同维度之间是有依赖存在的,比如生成数字5的时候,如果左边已经生成了数字5的左半部分,那么右半部分就几乎可以确定是5的另一半了。
因此一个好的想法是,生成模型在生成数字的时候有两个步骤,即(1)决定要生成什么数字,这个数字用一个被称为latent variable的向量z来表示,(2)然后再根据z来直接生成相应的数字。用数学表达式来表示就是:
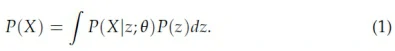
这就是所谓的latent variable model。
我们要介绍的VAE就是latent variable model的一种,我们将会看到,VAE可以利用BP算法来快速训练,且不需要对latent code的prior有任何知识,所有你需要的只是一个简单的encoder-decoder模型。也正是因为吸收了深度学习时代的众多技术优势,才使VAE变成了一个广受欢迎的生成模型。
VAE
latent variable
要解式(1),就必须决定P(z),然而latent variable z的prior是很难决定的,尤其是在深度学习背景下的生成模型,其生成的数据动辄上百维度,因此数据中就会存在大量依赖。
VAE是怎么解决这个问题的呢?它没有对z做出任何假设,而是说任何z的sample都可以从一个最简单的高斯分布来得到,即均值为0,协方差为单位矩阵的高斯分布。
你可能会觉得很奇怪,这是为什么呢?其实这里最关键的是注意到任何d维分布都可以从一个d维高斯分布+一个足够复杂的函数映射得到,比如我们可以把一个二维高斯分布映射成环型:
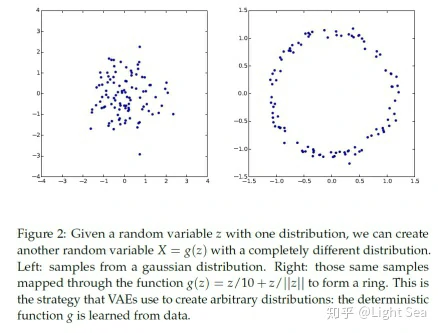
因此,只要有足够强力的函数估计器,我们就可以获得任何分布的latent variable z。很容易就可以想到用神经网络来构建这个函数估计器。
接下来的问题是,如何最大化(1)式?
The objective
有了z的prior,我们很容易想到利用多次采样的方式来最大化likelihood:
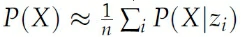
然而这种方法非常低效,特别是当z在高维空间的时候。
那么VAE是怎么解决这个问题的呢?
首先我们需要注意到,几乎所有的P(X|z)都是接近于0的,因为既然X是只有有限个类数据,那么z就应该有特定的值,因此我们要做的就是只用那些最有可能生成X的z来训练。这个时候我们就需要一个新的函数用来生成X对应的latent variable distribution:
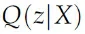
这个Q让我们可以计算
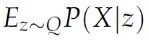
而不是z是高斯分布时候的期望,这就减少了计算量。然而,虽然这样很好,但是上式和P(X)又有什么关系呢?别忘了我们最终的目的是最大化P(X),因此这里我们就需要把这两个式子联系起来。
这里KL散度是一个比较好的选择,因为它刻画了两个分布之间的距离:
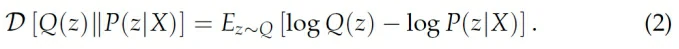
我们用贝叶斯公式来分解右边的P(z|X):
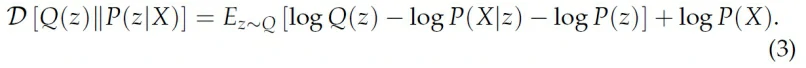
移项,两边乘-1就得到:
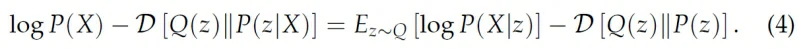
上式把Q(z)换成Q(z|X)就得到了VAE的objective:
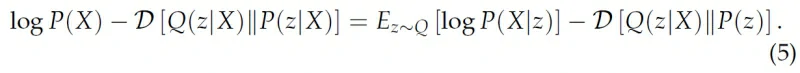
我们看到上式左边正是我们想优化的两项,即P(X)的likelihood和Q(z|X)估计P(z|X)的error。而右边也正好是我们可以计算的两项,第一项相当于一个decoder,第二项就相当于一个encoder。
上式右边一般被称为Evidence Lower Bound(ELBO),一般在讨论VAE的时候我们用ELBO来指代它的cost function。
Optimization 和 reparameterization trick
得到objective我们就需要做优化,这里我们首先需要得到Q(z|X),一般假设它满足一个高斯分布:
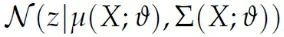
这里μ和Σ是任意的函数,一般用神经网络来拟合。
为了计算简便,我们一般假设Σ是对角矩阵,它的好处是让KL散度更好计算,两个多元高斯分布的KL散度是:
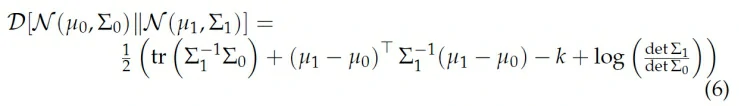
如果Σ是对角矩阵,则上式可化简为:
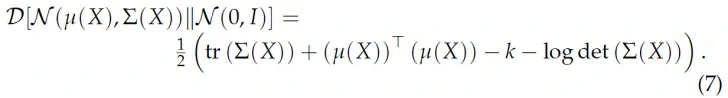
最终的cost function就是:
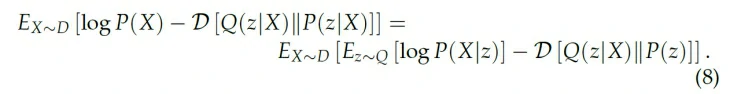
理论上来说我们需要sample多个z来估计上式,然而实际操作的时候我们用一次sample来作为估计值:
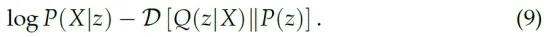
到这里你可能会觉得万事俱备只差代码了,然而等等,上式还有一个很致命的问题,即在sample z的时候,我们实际上做了一个不可导的计算,这会导致encoder和decoder之间无法传递梯度,但是在我们的假设中,z必须依赖于encoder Q,怎么解决这个问题呢?
这里解决的关键在于,我们不直接从Q编码得到的分布来sample z,而是先从一个标准正态分布采样一个值ε,然后通过Q得到的μ和Σ把这个值变换到Q得到的分布上:
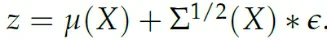
这样整个网络就是可导的,我们实际上的计算表达式是:
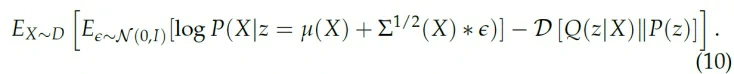
如下图所示:
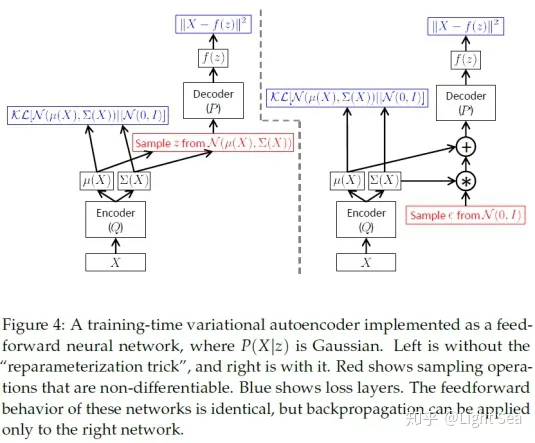
上述技巧被称为reparameterization trick,是一种非常有用的技巧。
Testing
当你训练好模型,想要生成一个新的数据的时候,你只需要保留decoder就可以,如下图所示:
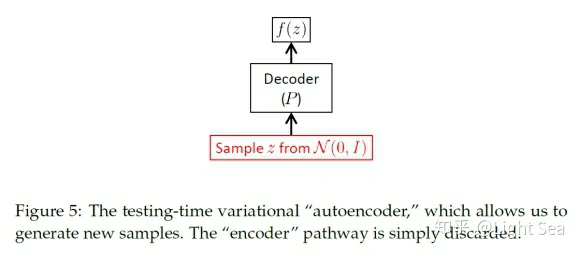
Conditional VAE
有的时候我们希望整个生成过程是基于某个条件的,这就是所谓的conditional VAE,其训练和测试图示如下图所示:
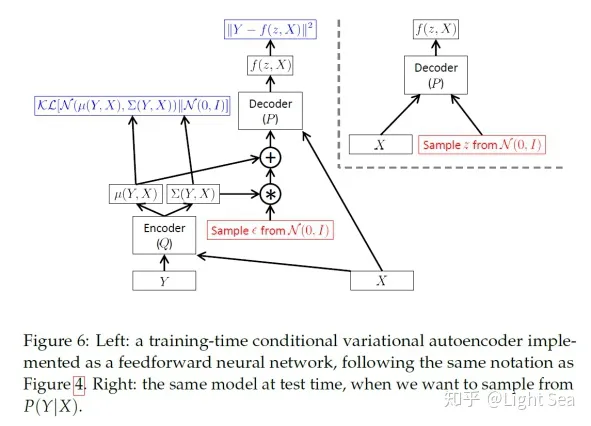
其objective的推导和VAE类似,只需要加上额外的条件即可:
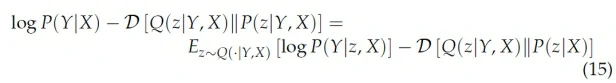
CVAE的一个典型应用是填补有缺失的图片,这时候缺失图片就是条件。
Conclusion
在这篇文章中介绍了VAE的数学原理和实现机制,研究者在之后也提出了性能更为优异的beta-VAE和beta-TCVAE等,有兴趣的同学可以了解一下。
参考资料
https://zhuanlan.zhihu.com/p/108262170
https://arxiv.org/abs/1606.05908