模型总览
AutoEncoder
在说VAE之前,先来看一下它的前身AutoEncoder(AE)。
AE是非常知名的自编码器,它通过自监督的训练方式,能够从原始特征获得一个潜在的特征编码,实现了自动化的特征工程,并且达到了降维和泛化的目的。
它的网络结构很简单,有编码和解码两个部分组成:
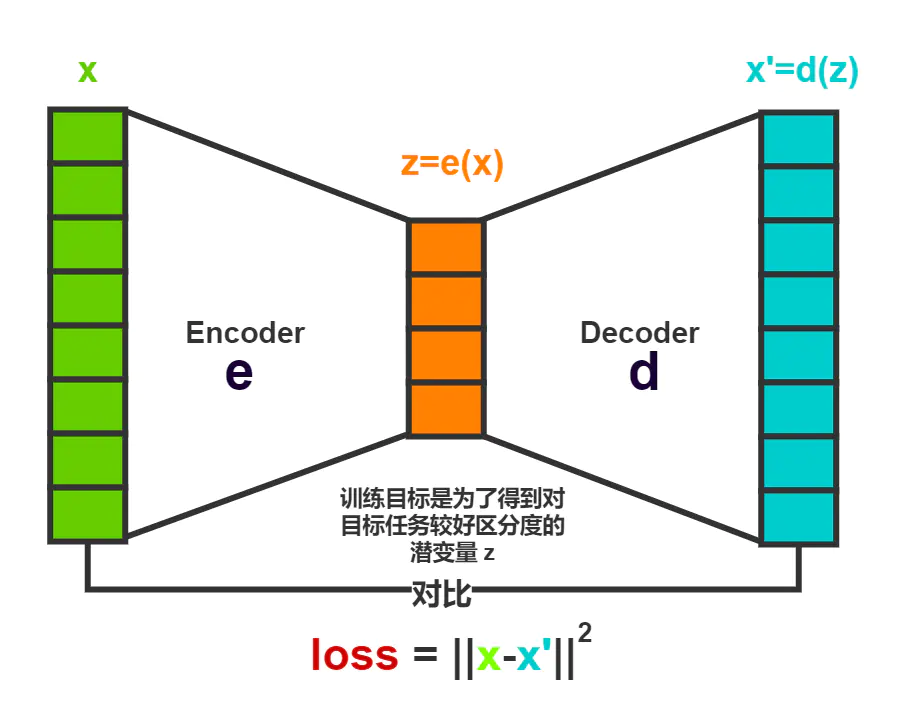
容易看出,之所以是自监督就是因为网络的target即是input本身,因此不需要额外的标签工作,虽然它由编码器和解码器两个部分组成,但是,显然从自编码器这个名字就可以看出,AE的重点在于编码,即得到这个隐藏层的向量,作为input的潜在特征,这是常见的一种embedding的一种方式。而解码的结果,基于训练目标,如果损失足够小的话,将会与input相同,从这一点上看解码的值没有任何实际意义,除了通过增加误差来补充平滑一些初始的零值或有些许用处。因为,从输入到输出的整个过程,都是基于已有的训练数据的映射,尽管隐藏层的维度通常比输入层小很多,但隐藏层的概率分布依然只取决于训练数据的分布,这就导致隐藏状态空间的分布并不是连续的,于是如果我们随机生成隐藏层的状态,那么它经过解码将很可能不再具备输入特征的特点,因此想通过解码器来生成数据就有点强模型所难了。
Variational AutoEncoder
正是因为以上的这些原因,有大佬就对AE的隐藏层做了些改动,得到了VAE。
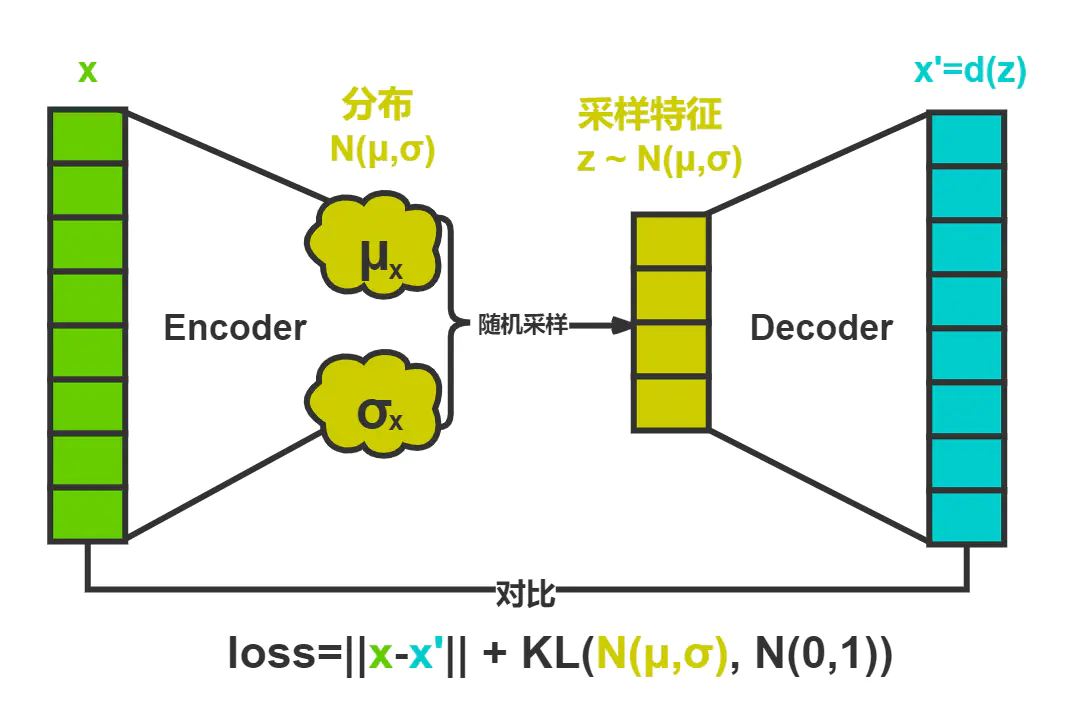
VAE将经过神经网络编码后的隐藏层假设为一个标准的高斯分布,然后再从这个分布中采样一个特征,再用这个特征进行解码,期望得到与原始输入相同的结果,损失和AE几乎一样,只是增加编码推断分布与标准高斯分布的KL散度的正则项,显然增加这个正则项的目的就是防止模型退化成普通的AE,因为网络训练时为了尽量减小重构误差,必然使得方差逐渐被降到0,这样便不再会有随机采样噪声,也就变成了普通的AE。
没错,我们先抛开变分,它就是这么简单的一个假设… 仔细想一下,就会觉得妙不可言。
它妙就妙在它为每个输入x,生成了一个潜在概率分布 p(z|x),然后再从分布中进行随机采样,从而得到了连续完整的潜在空间,解决了AE中无法用于生成的问题。
《论语》有言:“举一隅,不以三隅反,则不复也。” 给我的启发就是看事物应该不能只看表面,而应该了解其本质规律,从而可以灵活迁移到很多类似场景。聪明人学习当举一反三,那么聪明的神经网络,自然也不能只会怼训练数据。如果我们把原始输入看作是一个表面特征,而其潜在特征便是表面经过抽象之后的类特征,它将比表面特征更具备区分事物的能力,而VAE直接基于拟合了基于已知的潜在概率分布,可以说是进一步的掌握了事物的本质。
就拿一个人的某个行为来说,我们不能单纯看行为本身,因为这个行为往往代表了他的综合特性,他从出生开始,因为遗传,后天教育和环境,决定了他在面对某种情形的情况下,高概率会产生这个行为,也就是说掌握了概率分布,就掌控了一切。
这就好比..某个骚年A说他喜欢姑娘B,经过AE的编码得到的是A喜欢B类型的姑娘的特征,但是VAE编码之后就得到了更深入的特征:A馋B类型姑娘的身子。透过现象看本质,我想这便是VAE更胜一筹的原因。
变分自编码是怎么炼成的
读了上面的内容之后,你应该对VAE模型有了一个较为直观和感性的认知,但是可能会疑惑所谓的变分到底在哪里?
放心,变分并没有被作者吃掉,接下来,我们就从变分推断的角度,对VAE进行一个理性的推导。有了上面的基础,再读下面的内容时就会轻松愉快很多。
变分推断
变分自编码器(VAE)的想法和名字的由来便是变分推断了,那么什么是变分推断呢?
变分推断是 MCMC 搞不定场景的一种替代算法,它考虑一个贝叶斯推断问题,给定观测变量 x∈R^k 和潜变量 z∈R^d,其联合概率分布为 p(z, x) = p(z)p(x|z),目标是计算后验分布 p(z|x)。然后我们可以假设一个变分分布 q(z) 来自分布族 Q,通过最小化 KL 散度来近似后验分布 p(z|x):
这么一来,就成功的将一个贝叶斯推断问题转化为了一个优化问题~
变分推导过程
有了变分推断的认知,我们再回过头去看一下VAE模型的整体框架,VAE就是将AE的编码和解码过程转化为了一个贝叶斯概率模型:
我们的训练数据即为观测变量 x,假设它由不能直接观测到的潜变量 z 生成, 于是,生成观测变量过程便是似然分布:p(x|z),也就是解码器,因而编码器自然就是后验分布:p(z|x)。
根据贝叶斯公式,建立先验、后验和似然的关系:
接下来,基于上面变分推断的思想,我们假设变分分布 q_x(z),通过最小化 KL 散度来近似后验分布 p(z|x) ,于是,最佳的 q_x^* 便是:
因为训练数据 x 是确定的,因此 log~p(x) 是一个常数,于是上面的优化问题等价于:
此时,观察一下优化方程的形式…已经是我们前面所说的 VAE 的损失函数了
显然,跟我们希望解码准确的目标是一致的。要解码的准,则 p(z|x) 应该尽可能的小,编码特征 z 的分布 q_x(z) 同 p(z) 尽可能的接近,此时恰好 -log~p(x|z) 和 KL(q_x(z)||p(z)) 都尽可能的小,与损失的优化的目标也一致。
如何计算极值
正如前面所提到的AE潜变量的局限性,我们希望VAE的潜变量分布 p(z) 应该能满足海量的输入数据 x 并且相互独立,基于中心极限定理,以及为了方便采样,我们有理由直接假设 p(z) 是一个标准的高斯分布 N(0,1)。
编码部分
我们先来看一下编码部分,我们希望拟合一个分布 q_x(z) = N(μ, σ) 尽可能接近 p(z) = N(0, 1),关键就在于基于输入 x 计算 μ 和 σ,直接算有点困难,于是就使用两个神经网络 f(x) 和 g(x) 来无脑拟合 μ 和 σ。
值得一提的是,很多地方实际使用的 f(x)、g(x) 两部分神经网络并不是独立的,而是有一部分交集,即他们都先通过一个 h(x) 映射到一个中间层 h,然后分别对 h 计算 f(h) 和 g(h)。这样做的好处的话一方面是可以减少参数数量,另外这样算应该会导致拟合的效果差一些,算是防止过拟合吧。
解码部分
解码,即从潜变量 z 生成数据 x 的过程,在于最大化似然 p(x|z),那这应该是个什么分布呢?通常我们假设它是一个伯努利分布或是高斯分布。伯努利分布十分简单,熟悉的人也多,高斯分布接近大自然了,用起来又方便。
知道了分布类型,那计算 -log~p(x|z) 最小值其实只要把分布公式带进去算就可以了
高斯分布
和预期一样,演变为了均方误差。
伯努利分布
假设伯努利的二元分布是 P 和 1-P (注意这里是输出没一维组成的向量)
很对,正好就是交叉熵的损失。
然后,将编码和解码部分组合到一起,就形成了完整的VAE网络。
一点微不足道的技巧
训练的时候似乎出了点问题。从编码得到的分布 N(μ, σ) 随机采样 z 的这个过程没法求导,没法进行误差反向传播…
好在这里可以使用一个叫做重参数(reparametrisation trick)的技巧:
这样一来将采样变成了一个数值变换,整个过程便可导了
这样,训练好模型之后,我们可以直接将解码部分拿出来,通过标准高斯分布随机采样源源不断的生成数据了。
延伸的一些思考
VAE中使用神经网络来拟合高斯分布的想法独树一帜,对很多任务能带来启发。神经网络在特征化训练数据的过程无异于海量数据的管中窥豹,但是想要让模型超脱于豹,而像人一样产生对相似的猫、老虎…之类的概念,VAE的这种思想颇有一些意味。
参考资料
https://www.jianshu.com/p/ffd493e10751
Auto-Encoding Variational Bayes
Understanding Variational Autoencoders