范数
范数(Norm)是具有度量性质的函数,在机器学习中,经常用来衡量向量的大小。
范数把一个向量映射为一个非负值的函数,我们可以将一个向量x,经范数后表示点距离原点的距离,那么Lp范数定义如下:
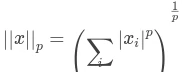
其中p属于R,p大于等于1。
经典范数
L0范数
表示统计向量中非零元素的个数(不是严格意义上的范数)
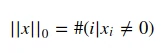
我们可以通过最小化L0范数,来寻找最少最优的稀疏特征项。但不幸的是,L0范数的最优化问题是一个NP hard问题(L0范数同样是非凸的)。因此,在实际应用中我们经常对L0进行凸松弛,理论上有证明,L1范数是L0范数的最优凸近似,因此通常使用L1范数来代替直接优化L0范数。
L1范数
表示零元素与非零元素差别非常重要时使用。例如:每当x中某个元素从0增加到m,则对应的L1范数也会增加m。也就是每个元素绝对值之和。也被称为是”稀疏规则算子”。
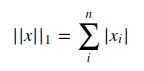
L2范数
欧几里得范数,表示从原点出发到向量x确定的点的欧几里得距离。在快接近源值时L2范数增长缓慢,对于区分恰好是零的元素和非零但值很小的元素的情况就不适用了(转为L1范数)。也就是通常说的欧氏距离。有人把它的回归叫“岭回归”(Ridge Regression),也有人叫它“权值衰减”(Weight Decay)。
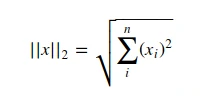
L∞范数
表示最大范数,只是统计向量中的最大值,也就是最大幅值的元素的绝对值。
Frobenius范数
类似于L2范数,用来衡量矩阵的大小。
总结
最后,两个向量的点积也可以用范数来表示:
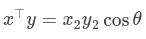
正则化
为何使用正则化?因为正则化可以避免过拟合的产生和减少网络误差。
表达式:
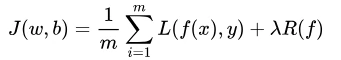
第一项表示经验风险,第二项表示正则项。
正则化与范数关系:R(f)就是相关范数表达式。
L1正则
凸函数,不是处处可微分。得到的是稀疏解(最优解常出现在顶点上,且顶点上的 w 只有很少的元素是非零的)。
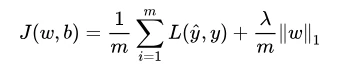
L2正则
凸函数,处处可微分,且易于优化。
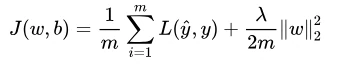
Dropout
Dropout是深度学习中经常采用的一种正则化方法。核心思想是减少神经元之间复杂的共适应性。当隐藏层神经元被随机删除之后,使得全连接网络具有了一定的稀疏化,从而有效地减轻了不同特征的协同效应。使神经网络中的某些神经元随机失活,让模型不过度依赖某一神经元,达到增强模型鲁棒性以及控制过拟合的效果。