几个基本概念
- 规范化参数:机器学习的模型拟合训练数据;
- 最小化误差:防止机器学习的模型与训练数据过度拟合;
- 范数:机器学习、深度学习等计算机领域内用的比较多的就是迭代过程中收敛性质的判断,一般迭代前后步骤的差值称为范数,用范数表示其大小。
常用的是二范数,差值越小表示越逼近实际值,可以认为达到要求的精度,收敛。范数本质是距离,存在的意义是为了实现比较。
机器学习中的范数
机器学习中为什么要使用范数
有监督的机器学习本质是 minimize your error while regularizing your parameters,也就是在规则化参数的同时最小化误差。最小化误差是为了让我们的模型拟合我们的训练数据,而规则化参数是防止我们的模型过分拟合我们的训练数据。
因为参数太多,会导致我们的模型复杂度上升,容易过拟合,也就是我们的训练误差会很小。但训练误差小并不是我们的最终目标,我们的目标是希望模型的测试误差小,也就是能准确的预测新的样本。所以,我们需要保证模型“简单”的基础上最小化训练误差,这样得到的参数才具有好的泛化性能(也就是测试误差也小)。
而模型“简单”就是通过规则函数来实现的。另外,规则项的使用还可以约束我们的模型的特性。这样就可以将人对这个模型的先验知识融入到模型的学习当中,强行地让学习到的模型具有人想要的特性,例如稀疏、低秩、平滑等等。要知道,有时候人的先验是非常重要的。前人的经验会让你少走很多弯路,这就是为什么我们平时学习最好找个大牛带带的原因。一句点拨可以为我们拨开眼前乌云,让人醍醐灌顶。对机器学习也是一样,如果被我们人为稍微点拨一下,它肯定能更快的学习相应的任务。只是由于人和机器的交流目前还没有那么直接的方法,目前这个媒介只能由规则项来担当了。
还有几种角度来看待规则化的。规则化符合奥卡姆剃刀(Occam’s razor)原理,它的思想很平易近人:在所有可能选择的模型中,我们应该选择能够很好地解释已知数据并且十分简单的模型。从贝叶斯估计的角度来看,规则化项对应于模型的先验概率。民间还有个说法就是,规则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项(regularizer)或惩罚项(penalty term)。
L0范数与L1范数
L0范数是指向量中非0的元素的个数。如果我们用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0。换句话说,让参数W是稀疏的。当下风风火火的“压缩感知”和“稀疏编码”的概念用的漫山遍野的“稀疏”就是通过这个思想来实现的。
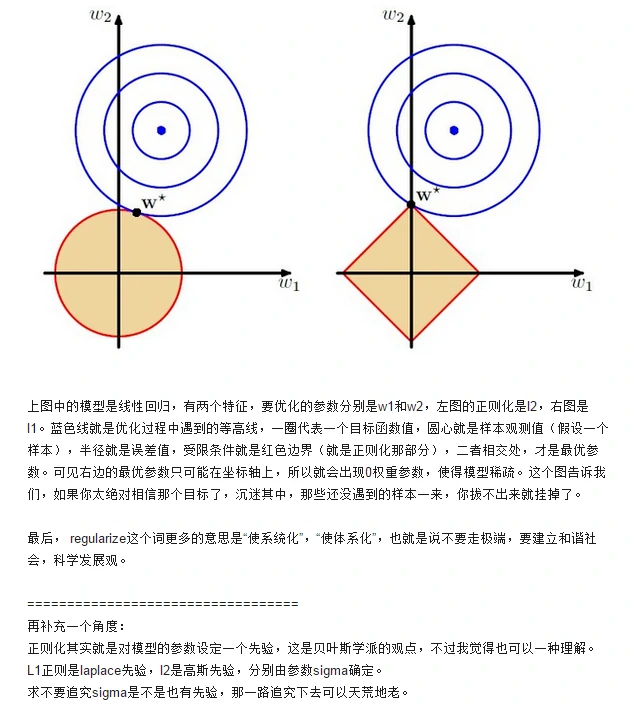
L1范数是指向量中各个元素绝对值之和,也有个美称叫“稀疏规则算子”(Lasso regularization)。为什么L1范数会使权值稀疏?有人可能会这样给你回答“它是L0范数的最优凸近似”。实际上,还存在一个更美的回答:任何的规则化算子,如果他在Wi=0的地方不可微,并且可以分解为一个“求和”的形式,那么这个规则化算子就可以实现稀疏。说是这么说,W的L1范数是绝对值,|w|在w=0处是不可微。后面会将L1和L2进行对比分析得出为什么L1可以实现稀疏。
既然L0可以实现稀疏,为什么不用L0,而要用L1呢?上面也提到了一是因为L0范数很难优化求解(NP难问题),二是L1范数是L0范数的最优凸近似,而且它比L0范数要容易优化求解。一句话总结:L1范数和L0范数可以实现稀疏,L1因具有比L0更好的优化求解特性而被广泛应用。
到这里,我们大概知道了L1可以实现稀疏,但我们会想,为什么要稀疏?让我们的参数稀疏有什么好处呢?
特征选择(Feature Selection)
大家对稀疏规则化前赴后继的一个关键原因在于它能实现特征的自动选择。一般来说,xi的大部分元素(也就是特征)都是和最终的输出yi没有关系或者不提供任何信息的,在最小化目标函数的时候考虑xi这些额外的特征,虽然可以获得更小的训练误差,但在预测新的样本时,这些没用的信息反而会被考虑,从而干扰了对正确yi的预测。
稀疏规则化算子的引入就是为了完成特征自动选择的光荣使命,它会学习地去掉这些没有信息的特征,也就是把这些特征对应的权重置为0。可解释性(Interpretability)
另一个青睐于稀疏的理由是,模型更容易解释。例如患某种病的概率是y,然后我们收集到的数据x是1000维的,也就是我们需要寻找这1000种因素到底是怎么影响患上这种病的概率的。假设我们这个是个回归模型:y=w1x1+w2x2+…+w1000x1000+b(当然了,为了让y限定在[0,1]的范围,一般还得加个Logistic函数)。通过学习,如果最后学习到的w就只有很少的非零元素,例如只有5个非零的wi,那么我们就有理由相信,这些对应的特征在患病分析上面提供的信息是巨大的,决策性的。也就是说,患不患这种病只和这5个因素有关,那医生就好分析多了。但如果1000个wi都非0,医生面对这1000种因素,累觉不爱。
L2范数
除了L1范数,还有一种更受宠幸的规则化范数是L2范数。它有两个美称,在回归里面,有人把有它的回归叫“岭回归”(Ridge Regression),有人也叫它“权值衰减”(weight decay)。它的强大功效是改善机器学习里面一个非常重要的问题:过拟合。过拟合就是模型训练时候的误差很小,但在测试的时候误差很大,也就是我们的模型复杂到可以拟合到我们的所有训练样本了,但在实际预测新的样本的时候,糟糕的一塌糊涂。通俗的讲就是擅长背诵知识,却不懂得灵活利用知识,应试能力很强,实际应用能力很差。
为什么L2范数可以防止过拟合?让L2范数的规则项最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0,这里是有很大的区别。而越小的参数说明模型越简单,越简单的模型则越不容易产生过拟合现象。
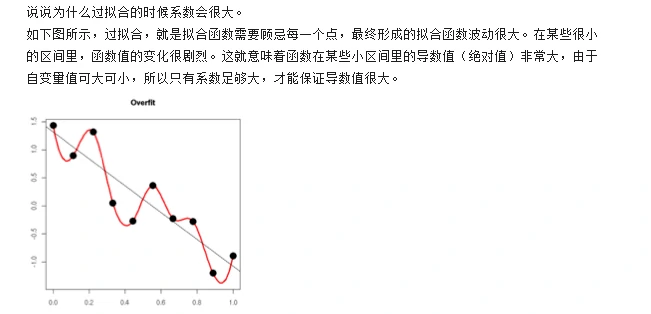
一句话总结下:通过L2范数,我们可以实现了对模型空间的限制,从而在一定程度上避免了过拟合。
L2范数的好处是什么呢?这里也扯上两点:
- 学习理论的角度:从学习理论的角度来说,L2范数可以防止过拟合,提升模型的泛化能力。
- 优化计算的角度:从优化或者数值计算的角度来说,L2范数有助于处理 condition number 不好的情况下矩阵求逆很困难的问题。
参考资料
https://blog.csdn.net/qq_26369907/article/details/89788593
https://blog.csdn.net/f156207495/article/details/82965093