第三章 无约束优化方法
本文是研究生课程《最优化方法》的复习笔记,主要是总结课件和相关博客的主要内容用作复习。
算法理论基础
- 无约束优化问题的最优性条件
先是一元函数取得极值的条件,高中就学过的

然后是拓展到多元函数后的理论

这三条和前面一元函数的三条是一一对应的,半正定对应大于等于,正定对应严格大于。
这里的最优性一直在说的都是局部最优性。
- 无约束凸规划问题的最优性条件
凸规划就有一个很好的特点,就是只要是局部最优解,那他就是全局最优解,也就是不存在鞍点了,再把前面的思路拓展就可以得到很好的结果了。

- 线搜索下降算法及其收敛性
- 算法
- 收敛性
- 收敛速度
后面的几种方法总览
参考:知乎: 最优化:线搜索中有最速下降法、牛顿法、拟牛顿法、共轭梯度法,那么他们分别时候用
Newton法利用了二阶梯度,收敛速度快,但是目标函数的Hesse矩阵不一定正定。于是出现了修正的Newton法,主要是对不同情况进行了分情况讨论。Newton法的优缺点都很突出。优点:高收敛速度(二阶收敛);缺点:对初始点、目标函数要求高,计算量、存储量大(需要计算、存储Hesse矩阵及其逆)。
共轭梯度法是介于最速下降法和牛顿法之间的一个方法,相比最速下降法收敛速度快,并且不需要像牛顿法一样计算Hesse矩阵,只需计算一阶导数(共轭梯度法是共轭方向法的一种,意思是搜索方向都互相共轭)。
拟Newton法是模拟Newton法给出的一个保优去劣的算法。
最速下降法
最速下降方向:
梯度的定义是:变化最快的方向,其实指向的就是上升最快的方向。
下降最快的方向是梯度的反方向,即−gk。
- 算法框架

- 优缺点

- 精确一维线搜索 + 最速下降法:


- 例题

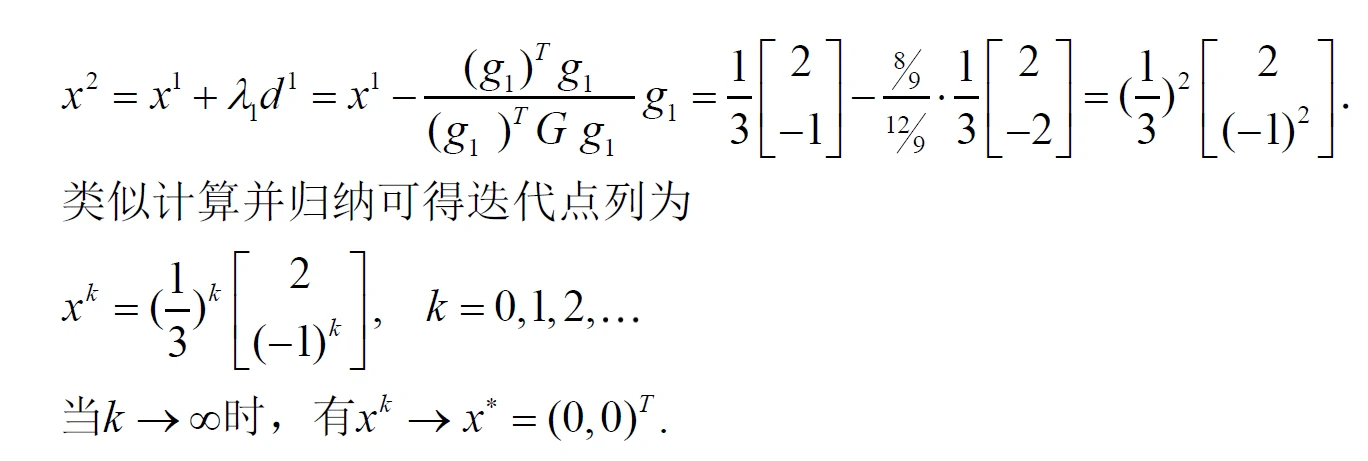
牛顿法
这里参考博客:https://blog.csdn.net/itplus/article/details/21896453
- 牛顿法与阻尼牛顿法



- 优缺点

- 例题

共轭梯度法
共轭方向法是介于最速下降法和Newton法之间的一种方法。克服了最速下降法的锯齿现象,从而提高了收敛速度;同时,共轭方向法的迭代公式比较简单,不必求目标函数的Hesse矩阵,比Newton法减少了计算量和存储量。是一种比较实用而且有效的方法。
- 共轭向量及其性质
关于共轭向量的定义:

满足上述条件后,称d0,d1,…,dk−1是G的共轭方向。
当Q=I时可以发现,d0,d1,…,dk−1相互正交。也就是说:正交是共轭的一种特殊情况,共轭是正交的推广。
- 共轭方向法的理论基础


用一句话概括那就是:
在精确一维线搜索的情况下,当前迭代点的梯度g与之前所有的搜索方向d正交。
- 共轭方向法的基本算法框架

如何构造共轭方向:Gram-Schmidt方法
二次函数极小化的共轭梯度法
前面是对共轭方向法+一维线搜索的整理,接下来对二次函数总结成共轭梯度法的理论。
- 【考】一般函数极小化的共轭梯度法
这部分可能是考试重点
例题比较简单


拟牛顿法
这里参考博客:
https://blog.csdn.net/songbinxu/article/details/79677948
https://blog.csdn.net/itplus/article/details/21896453
牛顿法中的Hesse矩阵HH在稠密时求逆计算量大,也有可能没有逆(Hesse矩阵非正定)。拟牛顿法提出,用不含二阶导数的矩阵 U_t 替代牛顿法中的 H^-1_t,然后沿搜索方向 −U_t g_t 做一维搜索。根据不同的 U_t 构造方法有不同的拟牛顿法。
注意拟牛顿法的关键词:
- 不用算二阶导数
- 不用求逆
- 拟牛顿条件


- 【重点】DFP算法与推导
DFP公式不用记


这里PPT里的结论是:


- DFP算法例题

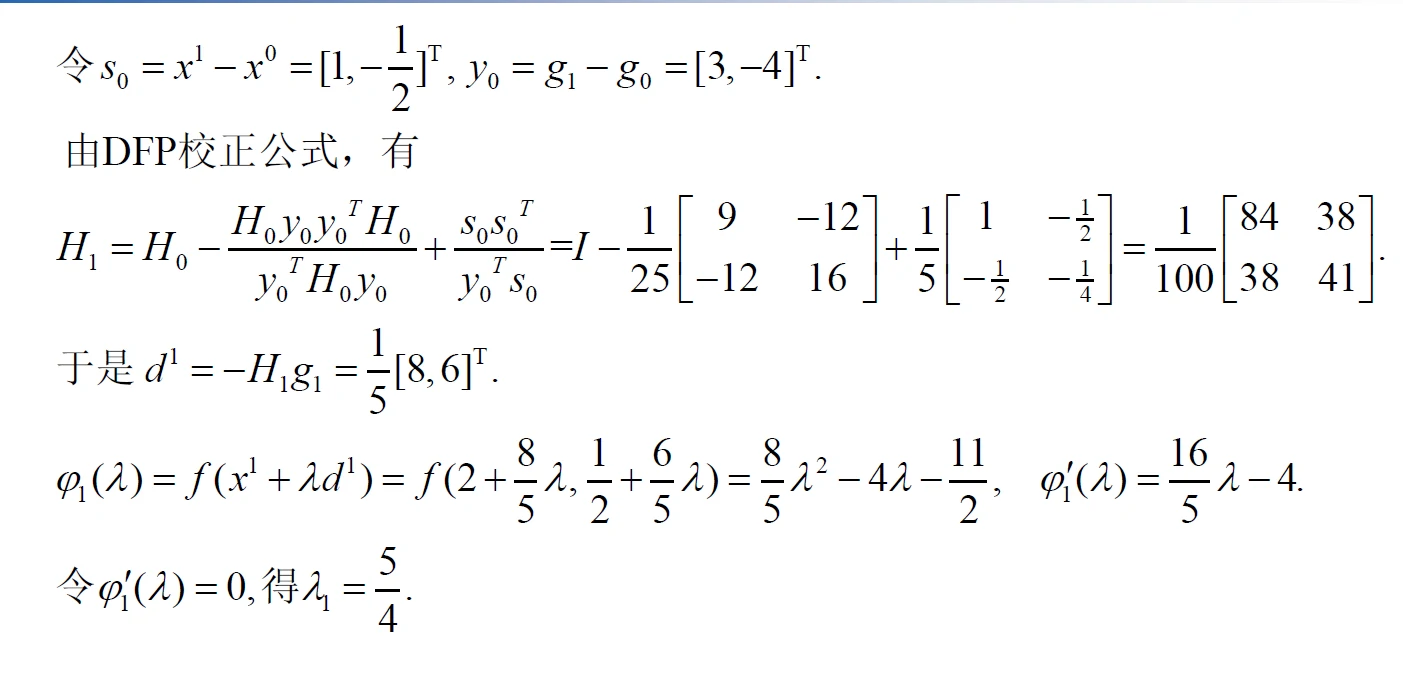

- BFGS算法


无约束优化-本章小结
- 方法总结
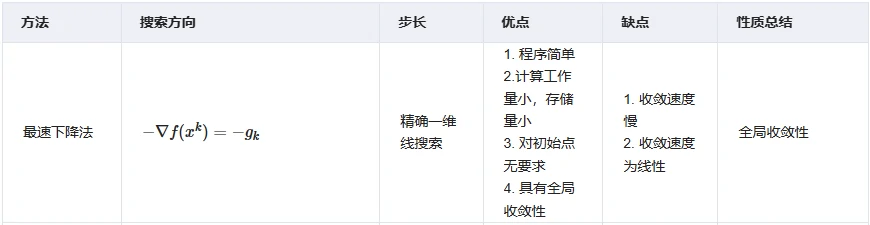




注:
关于收敛性参看第一章最后一节部分的内容
二次终止性:当一个算法用于求解严格凸二次函数极小值问题时,如果从任意初始点出发,算法经过有限步迭代后可达到函数的极小值点,则称该算法具有二次终止性。
参考资料
https://www.cnblogs.com/molinchn/p/13641437.html
https://www.zhihu.com/question/277576767
https://blog.csdn.net/itplus/article/details/21896453
https://blog.csdn.net/songbinxu/article/details/79677948
https://blog.csdn.net/itplus/article/details/21896453