第二章 线性规划
本文是研究生课程《最优化方法》的复习笔记，主要是总结课件和相关博客的主要内容用作复习。
线性规划的标准型
线性规划问题的解：
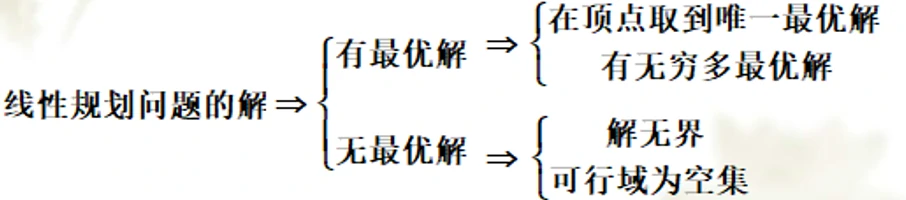
线性规划的基本概念
- （LP）是一个凸规划
- 基矩阵
- 由“基矩阵”发展而来的其他概念
- 基解
可行解是指满足条件，基本解是指基矩阵对应的解，两者同时满足为基本可行解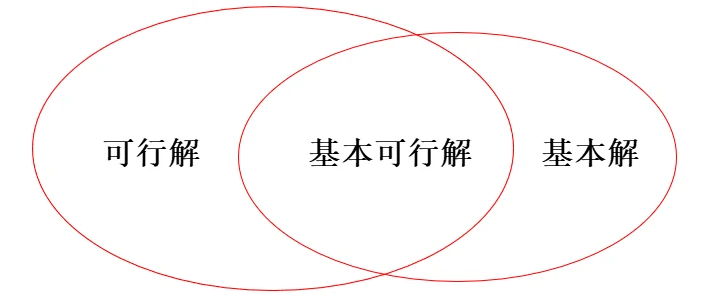
线性规划解的几何特征与规范式
定理 1：基可行解对应的A的列向量线性无关
定理 2：可行解是基可行解 <=>x是可行域的极点
定理 3：LP有可行解则必有基可行解
定理 4：LP如果有最优解，则必有某个基可行解是最优解
判别数的定义：
单纯形法的最优性判断
- 定理1：判断x0是LP的一个最优解
- 定理2：判断LP无最优解
基可行解的转换（入基，出基）
在3中转换后得到的新的目标函数值是下降的
【必考】单纯形法求解线性规划
做题
初始基可行解求法：大M法
- 构造辅助问题LP′
- LP′与LP的关系（最优解，无可行解，无最优解）
初始基可行解求法：二阶段法
- 第一阶段：求LP′′，然后判断原LP问题是否存在可行解
- 第二阶段：根据第一阶段得到的基可行解，用单纯型法求LP
【重点】线性规划的对偶理论
- 对偶规划概念与变形方法
- 对偶规划的性质
对合性
自由变量与等式约束的对等关系
- 对偶理论
- 最优性条件
