第一章 引论
本文是研究生课程《最优化方法》的复习笔记,主要是总结课件和相关博客的主要内容用作复习。
概述
预备知识
正定,半正定
本部分引自:https://zhuanlan.zhihu.com/p/44860862
正定和半正定这两个词的英文分别是positive definite和positive semi-definite,其中,definite是一个形容词,表示“明确的、确定的”等意思。

半正定与正定的主要关注点在于是否取得到等号,因此:

矩阵计算相关
矩阵梯度小结参考:https://zlearning.netlify.app/math/matrix/matrix-gradient.html
凸集,凸函数,凸规划
这里有很多定理,一个一个剖析
凸集
定义1.3.1 凸集,开凸集,闭凸集的定义
命题1.3.1 凸集的某些关系集合也为凸集
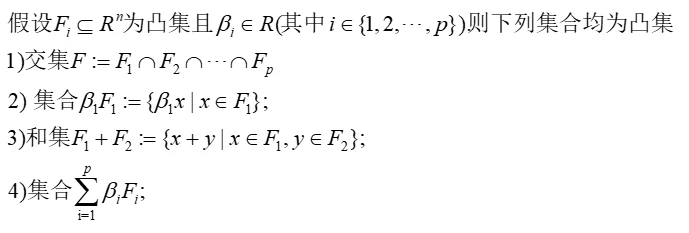
定理1.3.1 凸集中任意几点的组合仍然属于凸集
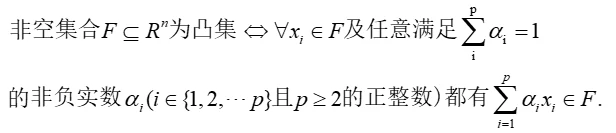
定义1.3.2 分离与严格分离的定义

定理1.3.2 不在凸集内的点可以被超平面严格分离
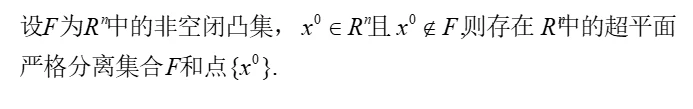
引理 1.3.1 Farkas引理
这里参考:https://zhuanlan.zhihu.com/p/29525513。对Farkas引理的几何意义理解有助于对该引理的直觉理解。
Farkas引理
设A是一个mxn阶的实矩阵,b是一个n维实向量,则下述两组方程中仅有一组有解:

其中x是n维实向量,y是m维实向量
几何解释
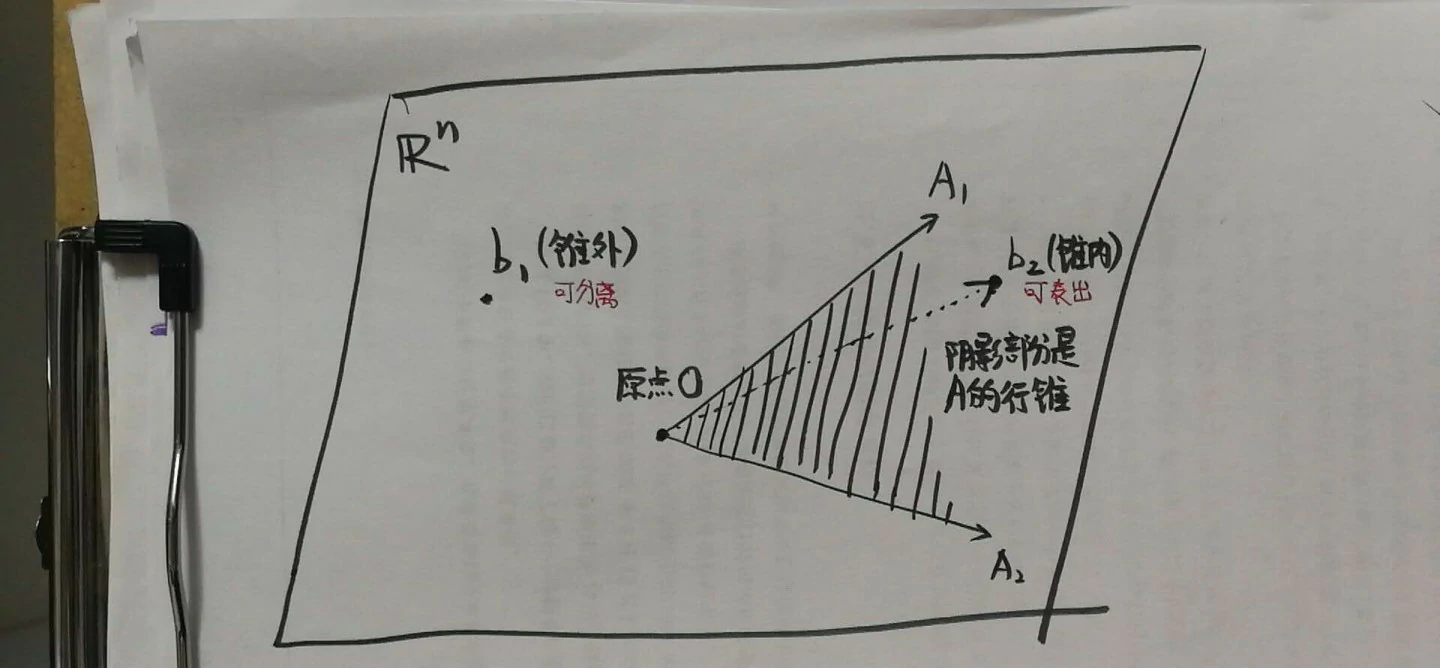
- 请见顶图,在空间Rn中,用矩阵A的行张成一个锥(张成锥与张成线性空间的区别就在于前者只能用非负的组合系数),即图中的锥OA1A2(阴影部分)
- 那么b的位置只可能有两种情形:(1)落在锥外;(2)落在锥内(含边界)
- 若b落在锥外:那么因为b点和A的行锥均为凸集,所以恰可利用凸集分离定理直接得到方程(1)
- 落b落在锥内:则b可以用A的行以非负系数线性表出,这恰是方程(2)
- 其实经典证明背后的思想就一句话:b点要么落在锥外,要么落在锥内
定理1.3.3 关于u0的组合表示

凸函数
定义 1.3.3:凸函数

定义 1.3.3:严格凸函数
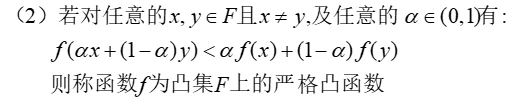
定义 1.3.3:强凸函数(一致凸函数)
强凸函数除了定义上的区别,还有哪些特性
命题 1.3.2 凸函数的性质

两个判别准则:
定理 1.3.4 一阶判别定理

定理 1.3.5 二阶判别定理

定理 1.3.6 强凸函数的判定定理
凸规划
定义1.3.4 凸规划

定理 1.3.7 凸规划的性质

1.4 线搜索迭代算法概述 及收敛性准则
- 线搜索迭代算法的一般框架

- 终止规则


- 迭代方向
- 迭代步长
精确一维线搜索
非精确一维线搜索(近似一维搜索)
- Goldstein型线搜索
- Armijo型线搜索
- Wolfe型线搜索(Wolfe-Powell型线搜索)
非单调一维线搜索
- Grippo-Lampariello-Lucidi非单调线搜索
- Zhang-Harger非单调线搜索
- Hu-Huang-Lu非单调线搜索
- 算法收敛性
收敛:如果算法是有限终止的,或所产生的迭代点列的每个聚点是优化问题的最优解,则称该算法是收敛的。
全局收敛与局部收敛:如果对于任意的初始点x0,算法是收敛的,则称该算法是全局收敛的。如果只有初始点x0充分靠近最优解时,算法是收敛的,则称该算法是局部收敛的。
收敛速率:


参考资料
https://www.cnblogs.com/molinchn/p/13641403.html
https://zhuanlan.zhihu.com/p/44860862
https://zlearning.netlify.app/math/matrix/matrix-gradient.html
https://zhuanlan.zhihu.com/p/29525513