原文
论文链接:https://www.nature.com/articles/s41586-021-04086-x.pdf
总览
2021年12月2日的 nature 封面文章,如何用机器学习帮助数学公式的证明?
标题:AI 辅助的直觉
ML 模型不难,从 ML 角度有提升空间
- 近 100 行代码 83%;AutoGulon 不到 10 行代码,97%;可解释性损失
Nature 封面文章,增大房子的面积,ML 在别的领域盖房子
- 研究新领域的重要问题 eg. ML 筛选出数学变量最重要的部分,数学家根据重要的变量 来猜想变量之间的关系
ML 模型的改进:把房子加高
Nature (周刊:新闻、观点、原创性的研究工作) 和 science 一流期刊
- 包含所有科学研究的话题,AI 领域一年发不到 10 篇
- 图很好看,质量高
本文的标题:通过 AI 来指导人类的直觉、来推进数学的发展
Open access:开源、任意下载;影响力会更大
AI 怎么在数学定理的发现中起到作用的呢?
本文的 ML 和 数学两个问题:topo 拓扑学 和 表示论
技术细节在 appendix 里
标题和作者
AI 来指导人的直觉从而推进数学的进展
审稿快 < 3月:7月10号投稿、9月30号接受
作者多:DeepMind + 数学家的单位
- 2个通讯作者:
- 一作:干活
- 最后一个作者:项目的技术负责人
- 倒数第二个作者:DeepMind 的 CEO, 21 nature 文章 based on google scholar
- Science 少一点,nature 和 DeepMind 总部都在英国
- 编辑的对可靠的研究者的稿件的处理优先级 会高一些 —> 2个多月接受 + nature 封面
- 数学家贡献排名稍后,本文的数学结论已发表
摘要
数学套路:发现一些模式、把这些模式公式化 or 证明一些猜想,最后推导定理
- 先有结论、提出猜想;再试图证明猜想
- 数学归纳法:n=1、2、3的简单例子,找规律;泛化到 n 的情况;再试图证明结论
- 数学有很多公开的、未解决的问题
AI套路:拿点数据、跑跑实验、看看实验结果;根据结果找可解释性的结论
1960 年 已经有数学家用计算机辅助来发现模式和公式化猜想
- BSD猜想,千禧年 2000年 (美国克雷数学研究所 (Clay Mathematics Institute,CMI))提出的七大问题之一
- BSD 猜想,数学家用计算机辅助计算一些简单的情况,从而抽象出一个更一般的结论
- 只有庞加莱猜想被解决
- 1900 年 希尔伯特提出了23个猜想,推动数学的发展
计算机辅助数学计算的例子
- 图论:按照某种性质的图有多少个,计算机遍历所有的组合、统计结果;根据计算得到的图个数结果,猜想数学结论
- Richard 计算机理论研究者,一个算法的复杂度的上下限,通过计算机模拟逼近曲线的形状,然后猜想数学结论 or 证明的思路是什么
摘要 1 + 2 句 == 背景
细化本文主题:2个例子显示了 ML 对数学领域的结论的证明的有用性
本文觉得应该如何用 ML 来帮助数学家发现新的猜想 or 定理?
- ML 发现潜在的猜想 or 定理模式和数学对象之间的关系
- 归因技术找到最重要的数学对象,数学家可以着重考虑这几个重要的成份
本文主旨:提供 ML 帮助数学猜想的 framework
examples:结 knot(面粉团的捏出来的各个样子都是等价的;代数结构和几何结构的关系);对称群的组合不变猜想()
本文 level:搭建了数学家和 ML 之间的桥梁,吸收优势,促进领域发展
本文有 2 个故事讲述 ML 辅助发现 拓扑结 和 表示论 的数学结论
- 数学门槛有一点高,需要理解数学名词
- ML 用到别的领域 or 任何一个领域的技术拓展应用到别的领域时,都希望有该领域的基础知识
导论
导论第一段:
数学套路:发现一些模式、提出一些猜想
- 猜想是什么呢?可能是真、or 在有些情况还没有被证实为真的一些命题
- 定理是什么?数学的美;数学定理可以覆盖所有的东西
- CS 代码写出思想 by 几行代码;可能几百行代码处理各种情况的 corner cases
数学家和数据、计算机、AI的关系是什么呢?
- 数据辅助:高斯 根据手算质数表 提出 质数定理
- 计算机辅助:bsd 猜想;or 计算机来计算 Π 的一万位
- 但 AI 没有特别帮助 数学家
本文的 motivation 是什么?常见句式
- 之前的结果 好 且 有用,但无法一般化的推广
- 结果不错 + 一般化,但是没有重要的结果被发现
- 常见句式:
- 前人工作效果好、但不够一般化;本文更加一般化
- 前人工作可以处理很一般的情况,但结果不够好;本文结果更好
- 我的工作和这两类工作都不一样
导言第二段:AI 在数学的应用
AI 在数学领域能够干什么呢?
- AI 搜索空间可以很广、为数学猜想提供反例
- 数学猜想有一个反例,猜想不成立;和 cs 不同,打一个补丁 if else 即可
- 生成一些 symbolic solutions 计算软件 mathematica
- 在一些数学物体里找 一些特别的架构
本文和已有工作的不同是什么?
AI 帮助发现定理和猜想,夸张 example:AI 帮你写数学论文
- 之前的工作,在某一块 or 方面 辅助数学家做一些事情
告诉数学家,有一个很强大的工具,可以帮你证明顶里,快来用!
有监督的学习 AI 发现了 2个 新的定理!
框架
AI 指导数学的直觉
数学的直觉 在 数学研究中很重要
- Terry tao(陶哲轩 Terence Chi-Shen Tao,澳籍华人数学家)博客中的一句话
- 复杂的数学问题 需要 严谨的公式化 + 好的直觉
- 大胆假设、仔细求证
本文描述了一个一般化的方法,数学家使用 ML 工具 来帮助定理发现
数学家的直觉:需要思考 2个 不同的数学物体之间的联系,猜 x(z) 和 y(z) 的联系
- z 是某一个特定的物体
- X(z) 表示的是在某一些方面对 z 的刻画
- Y(z) 表示的是另外一些数学概念对 z 的刻画
ML 怎么描述 x(z) 和 y(z) 的联系呢?
- 用一个函数 f, x(z) 是输入特征, y(z) 是输出标签。
- 如果 ML 可以学到一个函数 f,可以告诉数学家 x(z) 和 y(z) 是有联系的
Example ML 描述 2个 数学对象之间的联系
- Z 是一个凸的多面体;多面体 i.e., 正方体
- x(z) 是 (顶点数 int、边数 int、体积 R、表面积 R)
- y(z) 是 凸多面体 z 的 面 的数量
x(z) * (-1, 1, 0, 0) + 2 = y(z)
凸多面体的边数 - 其定点数 + 2 = 该凸面体的面数
线性回归:和一个 四维向量 做点积 + 2
ML 学习 1个 四维的常数值,得到学习的常数值后,用严格的数学推理来证明猜想
更复杂的例子,ML 要学的函数 f 更复杂、维度更高;需要更复杂的机器学习模型
一篇新闻
作者 | Ben Dickson
译者 | Sambodhi
DeepMind 研究人员最近发表了一篇题为《通过用人工智能引导人类直觉来推进数学》(Advancing mathematics by guiding human intuition with AI)的论文,认为深度学习能够帮助发现被人类科学家忽视的数学关系。很快,这篇论文在科技媒体上引起了广泛的关注。
一些数学家和计算机科学家对 DeepMind 的工作及其论文中所取得的成果表示赞赏,称其具有突破性。其他人则对此持怀疑态度,认为这篇论文和它在大众媒体上的报导,可能夸大了深度学习在数学中的应用。
一种基于机器学习的数学发现框架
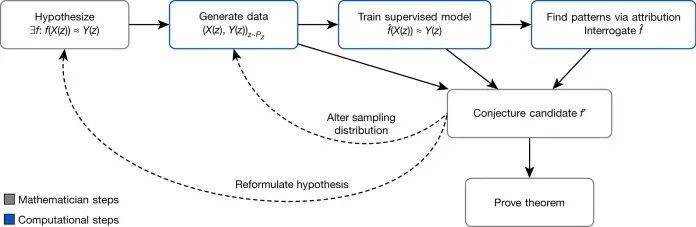
数学家们首先对两个数学对象之间的关系做出假设。为了验证这一假设,他们使用计算机程序为这两种类型的对象生成数据。接下来,一种监督式机器学习模型算法对这些数字进行计算,并尝试调整其参数,将一种类型的对象映射到另一种类型的对象。
研究人员写道:“在这个回归过程中,机器学习最重要的贡献在于,只要有足够的数据,就可以学习到一系列可能的非线性函数。”
如果训练过的模型比随机猜测的表现更好,那么它可能表明这两个数学对象之间确实存在着可发现的关系。通过使用不同的机器学习技术,研究人员能够发现与问题更相关的数据点,改进他们的假设,生成新的数据,并训练新的模型。通过重复这些步骤,他们可以缩小合理猜想的范围,并加速得到最终解决方案。
DeepMind 的科学家将该框架描述为“直觉的试验台”,它可以快速验证“关于两个量之间关系的直觉是否值得追求”,并为它们可能存在的关系提供指引。
利用这个框架,DeepMind 的研究人员通过使用深度学习得出了“两项基本的新发现,一项是拓扑学,另一项是表示论。”
这项工作的一个有趣之处在于,无需庞大的算力,而算力已经成为 DeepMind 研究的支柱。根据该论文,在这两项发现中使用的深度学习模型可以在“一台只有一个图形处理单元的机器上”在几个小时内进行训练。
纽结与表示
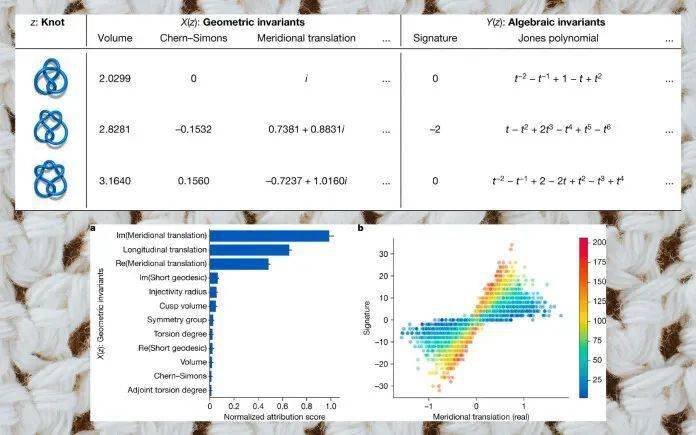
纽结是空间中的一条闭合曲线,可以用各种方式定义。随着其交叉点数量的增加,它们将会变得更复杂。研究人员想看看他们是否可以利用机器学习来发现代数不变量和双曲不变量之间的映射,这是定义纽结的两种根本不同的方式。
研究人员写道:“我们假设,在一个纽结的双曲不变量和代数不变量之间存在一种未被发现的关系。”
使用 SnapPy 软件包,研究人员可以生成“签名”、1 个代数不变量和 12 个有希望的双曲不变量,可用于 170 万个纽结,最多有 16 个交叉点。
接下来,他们创建了一个全连接的前馈神经网络,这个网络具有三个隐藏层,每个隐藏层有 300 个单元。他们训练深度学习模型,将双曲不变量的值映射到签名上。他们的初始模型能够以 78% 的准确率预测签名。通过进一步的分析研究,他们在双曲不变量中发现了一个较小的参数集,可以预测签名。研究人员完善了他们的猜想,生成了新的数据,重新训练了他们的模型,并得出了一个最终的定理。
研究人员将该定理描述为“连接纽结的代数和几何不变量的首批结果之一,它有着很多有趣的应用。”
“我们预计,在低维拓扑学中,这种新发现的自然斜率和签名之间的关系将会有许多其他应用。”研究人员写道:“如此简单而又深刻的关系,在这个早已被广泛研究的领域里却被忽视了,真是太不可思议了。”
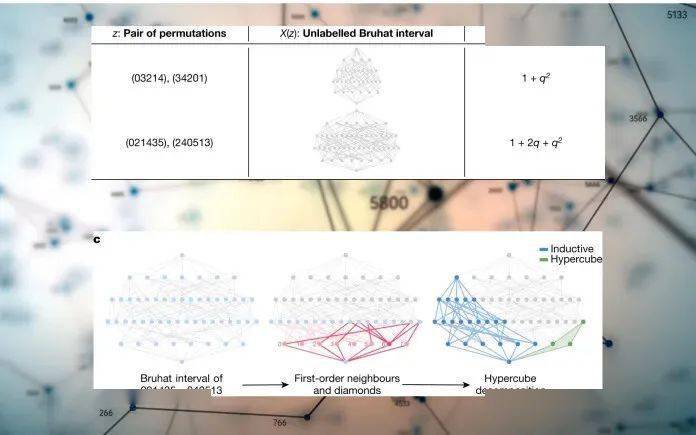
论文的第二个结果也是对称性的两种不同观点的映射,它的复杂性远远超过了纽结。
在本例中,他们使用了一种图神经网络(graph neural network,GNN),以求 Bruhat 区间图和 Kazhdan-Lusztig(KL)多项式之间的关系。图神经网络的一个好处就是能够对庞大的、单凭头脑难以处理的图进行计算和学习。深度学习将区间图作为输入,尝试预测相应的 KL 多项式。
同样,通过生成数据,训练深度学习模型,并重新调整过程,科学家们能够得出一个可证明的猜想。
大众对 DeepMind 数学人工智能的反应
谈到 DeepMind 在纽结理论方面的发现,内布拉斯加大学林肯分校的纽结理论家 Mark Brittenham,在接受《自然》(Nature)采访时说:“作者用一种很直接的方法,证实了不变量是相关的,这一事实告诉我们,在这一领域中,存在着许多我们尚未充分了解的、非常基本的事物。”Brittenham 还说,DeepMind 的这项技术在发现惊人的联系上,比起其他将机器学习应用于纽结的努力,它是很新颖的。
以色列特拉维夫大学的数学家 Adam Zsolt Wagner 也接受了《自然》杂志的采访,他说,DeepMind 提出的方法可以证明对某些类型的问题有价值。
Wagner 有将机器学习应用于数学的经验,他称:“如果没有这种工具,数学家可能就会花上好几个星期甚至几个月去证明某个公式或者定理,而这些公式和定理最后都会被证明是错误的。”但他也补充说,目前还不清楚它的影响会有多广泛。
持怀疑态度的理由
继 DeepMind 的研究成果在《自然》杂志上发表后,纽约大学计算机科学教授 Ernest Davis 发表了一篇自己的论文,就 DeepMind 关于结果的框架以及深度学习在普通数学中的应用的局限性提出了一些重要问题。
关于 DeepMind 的论文中提出的第一个结果,Davis 观察到,纽结理论并不是深度学习优于其他机器学习或统计方法的典型问题。
纽结问题只有 12 个输入特征,其中只有三个是相关的。而输入特征和目标变量之间的数学关系很简单。
Davis 写道:“很难理解为什么有 20 万个参数的神经网络会成为首选的方法;简单、传统的统计方法或支持向量机更适合。”
在第二个项目中,深度学习的作用更为重要。“与使用通用深度学习架构的纽结理论项目不同,神经网络被精心设计,以满足对这个问题更深层次的数学知识。此外,深度学习在预处理数据上比在原始数据上工作得更好,错误率大约是 1/40。”他写道。
Davis 称,一方面,这些研究结果与那些批评的观点形成了鲜明的对比,即把领域知识纳入深度学习中是非常困难的。他写道:“另一方面,深度学习的爱好者经常称赞深度学习是一种‘即插即用’的学习方法,它可以用原始数据来解决手头的任何问题;这与这种赞誉相悖。”
在这些任务中,要成功应用深度学习,可能在很大程度上依赖于训练数据的生成方式和数学结构的编码方式。这说明该框架可能适用于一小类数学问题。
“寻找生成和编码数据的最佳方式涉及理论、经验、艺术和实验的混合。这一切的重担都落在了人类专家身上,”他写道。“深度学习可以是一种强大的工具,但也不是万能的。”
Davis 提醒道,在当前关于深度学习的炒作氛围中,“存在着一种异常的动机,让人们关注深度学习在这项研究中的作用,而不只是 DeepMind 的机器学习专家,甚至是数学家。”
Davis 总结说,就像在这篇文章中所提到的,深度学习最好被视为“实验数学工具箱中的另一种分析工具,而非一种全新的数学方法。”
值得注意的是,原始论文的作者也指出了他们的框架的一些局限性,例如“它需要生成对象表示的大型数据集的能力,并且模式在可计算的示例中是可检测的。此外,在某些领域,在这个范式中可能很难学习到感兴趣的函数。”
深度学习与直觉
其中一个争议主题是,该论文宣称,深度学习是“引导直觉”。Davis 形容这一说法是“非常不准确的描述,即对数学家在使用这样的深度学习时,得到了或者期望得到什么帮助。”
直觉是人类和人工智能的重要区别之一。这是一种比随机猜测更好的决策能力,并且在大部分时间里,它可以引导你走上正确的方向。正如迄今为止人工智能的历史所显示的那样,在海量数据中,并没有预定义的规则和模式能够捕捉到直觉。
“在数学的世界中,‘直觉’一词意味着,一个概念或证明可以建立在人们对熟悉的领域(如数字、空间、时间或运动)根深蒂固的感觉上,或者以某种其他方式‘有意义’或‘似乎正确’,而不需要明确的计算或逐步推理。”Davis 写道。
Davis 认为,为了获得对数学概念的直观掌握,往往需要通过多个具体的例子来进行,但这并非统计学上的相关工作。换句话说,你不会通过运行数百万个例子和观察某些模式重复出现的百分比来获得直觉。
这意味着,并不是深度学习模型让科学家直观地理解他们所定义的概念、所证明的定理以及所提出的猜想。
Davis 写道:“深度学习所做的,是给他们提供一些建议,告诉他们问题的哪些特征看起来重要,哪些看起来不重要。这并不值得嗤之以鼻,但也不应该被夸大。”
原文链接
https://bdtechtalks.com/2021/12/13/deepminds-machine-learning-mathematics/