论文阅读-FCN全卷积网络论文阅读及代码实现

Full Convolutional Networks 即全卷积神经网络，这是 2015 年的一篇语义分割方向的文章，是一篇比较久远的开山之作。它是语义分割方向的鼻祖，后面的文章很多都借鉴了这篇文章的思想，掌握好基础我们才能飞的更高。本篇文章分为两部分: 论文解读与代码实现。

FCN 论文链接：https://arxiv.org/pdf/1411.4038.pdf

---

论文解读

语义分割介绍

语义分割（Semantic Segmentation）的目的是对图像中每一个像素点进行分类，与普通的分类任务只输出某个类别不同，语义分割任务输出是与输入图像大小相同的图像，输出图像的每个像素对应了输入图像每个像素的类别。

---

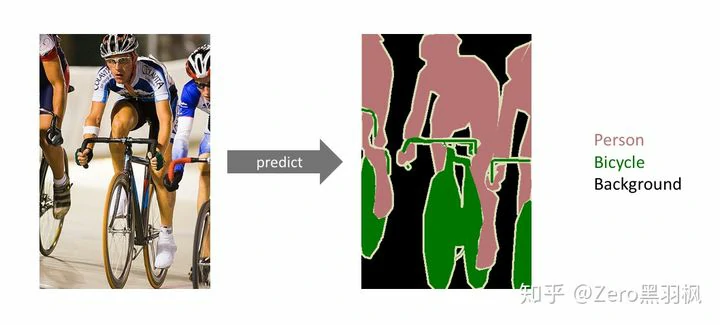
网络结构

FCN 的基本结构很简单，就是全部由卷积层组成的网络。用于图像分类的网络一般结构是卷积-池化-卷积-池化-全连接，其中卷积和全连接层是有参数的，池化则没有参数。论文作者认为全连接层让目标的位置信息消失了，只保留了语义信息，因此将全连接操作更换为卷积操作可以同时保留位置信息及语义信息，达到给每个像素分类的目的。网络的基本结构如下:

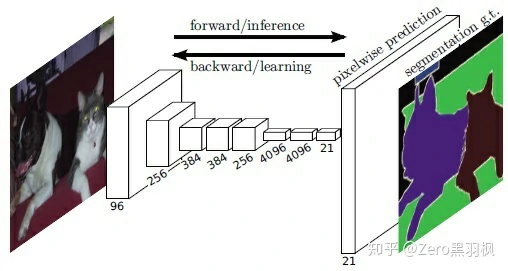
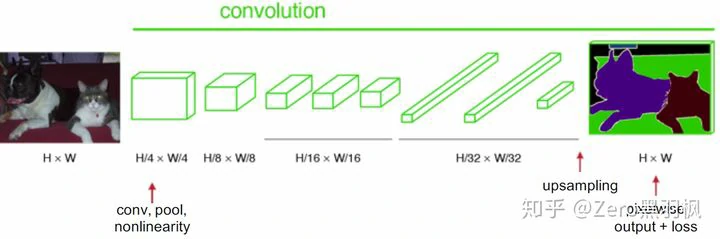
输入图像经过卷积和池化之后，得到的 feature map 宽高相对原图缩小了数倍，例如下图中，提取特征之后”特征长方体”的宽高为原图像的 1/32，为了得到与原图大小一致的输出结果，需要对其进行上采样（upsampling），下面介绍上采样的方法之一-反卷积（图中最终输出的”厚度”是 21，因为类别数是 21，每一层可以看做是原图像中的每个像素属于某类别的概率，coding 的时候需要注意一下）。

---

反卷积

反卷积是上采样（unsampling）的一种方式，论文作者在实验之后发现反卷积相较于其他上采样方式例如 bilinear upsampling 效率更高，所以采用了这种方式。

关于反卷积的解释借鉴了这一篇：https://medium.com/activating-robotic-minds/up-sampling-with-transposed-convolution-9ae4f2df52d0，英文 OK 的小伙伴推荐看原文，讲的很通透。

先看看正向卷积，我们知道卷积操作本质就是矩阵相乘再相加。现在假设我们有一个 4x4 的矩阵，卷积核大小为 3x3，步幅为 1 且不填充，那么其输出会是一个 2x2 的矩阵，这个过程实际是一个多对一的映射：

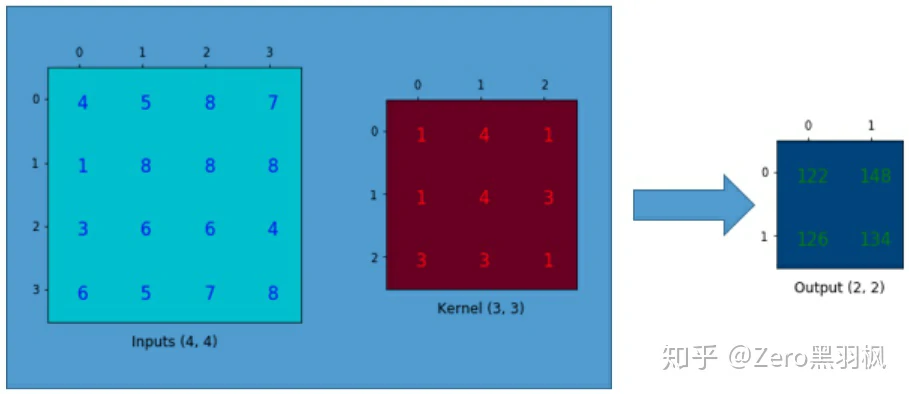
从上图也可以看出，卷积操作其实是保留了位置信息的，例如输出矩阵中左上角的数字”122”就对应了原矩阵左上方的 9 个元素。

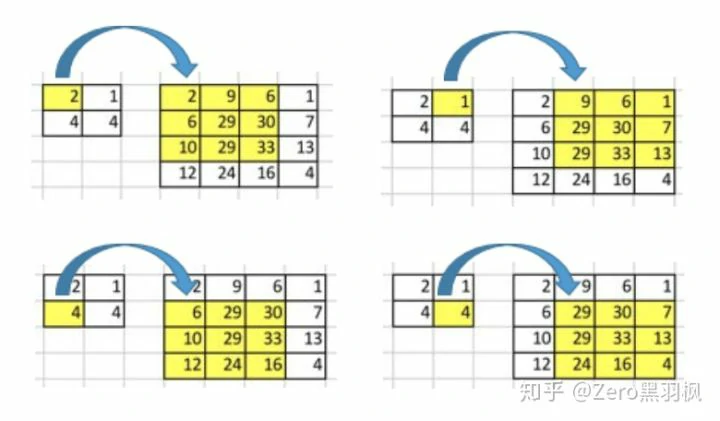
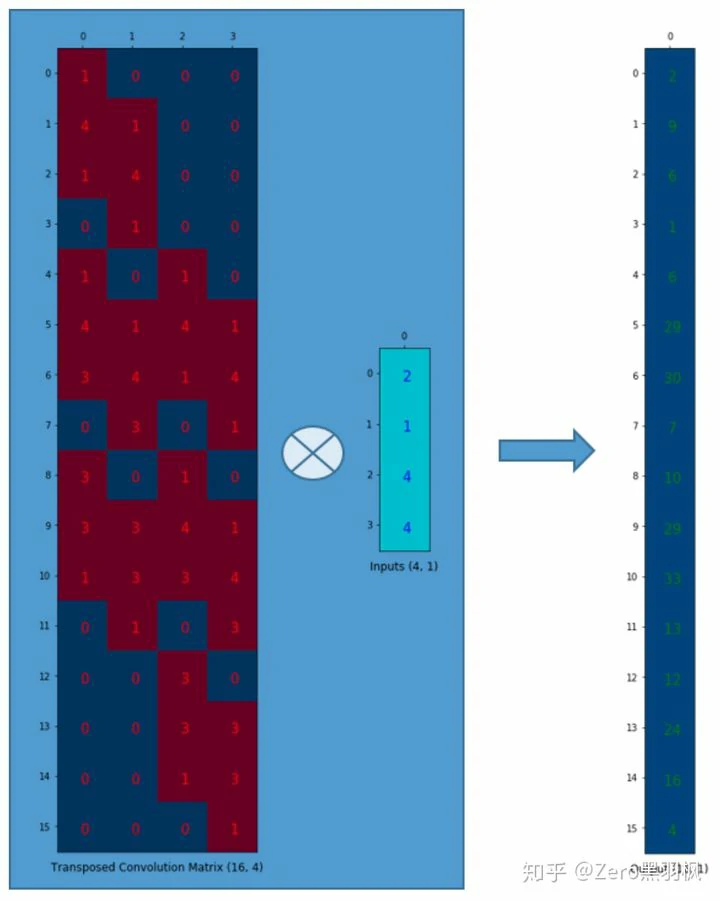
那么如何将结果的 2x2 的矩阵”扩展”为 4x4 的矩阵呢(一对多的映射)。4x16 的卷积核矩阵与 16x1 的输入矩阵相乘，得到了 4x1 的输出矩阵，达到了多对一映射的效果，那么将卷积核矩阵转置为 16x4 乘上输出矩阵 4x1 就可以达到一对多映射的效果，因此反卷积也叫做转置卷积。具体过程如下:

总结来说，全卷积网络的基本结构就是”卷积-反卷积-分类器“，通过卷积提取位置信息及语义信息，通过反卷积上采样至原图像大小，再加上深层特征与浅层特征的融合，达到了语义分割的目的。

---

代码实现

大佬实现了简单版本的 FCN，代码地址 github

VGG16 网络代码，forward 返回了卷积过程中各层的输出，以便后面与反卷积的特征做融合：

class VGG(nn.Module):
    def __init__(self, pretrained=True):
        super(VGG, self).__init__()

        # conv1 1/2
        self.conv1_1 = nn.Conv2d(3, 64, kernel_size=3, padding=1)
        self.relu1_1 = nn.ReLU(inplace=True)
        self.conv1_2 = nn.Conv2d(64, 64, kernel_size=3, padding=1)
        self.relu1_2 = nn.ReLU(inplace=True)
        self.pool1 = nn.MaxPool2d(kernel_size=2, stride=2)

        # conv2 1/4
        self.conv2_1 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
        self.relu2_1 = nn.ReLU(inplace=True)
        self.conv2_2 = nn.Conv2d(128, 128, kernel_size=3, padding=1)
        self.relu2_2 = nn.ReLU(inplace=True)
        self.pool2 = nn.MaxPool2d(kernel_size=2, stride=2)

        # conv3 1/8
        self.conv3_1 = nn.Conv2d(128, 256, kernel_size=3, padding=1)
        self.relu3_1 = nn.ReLU(inplace=True)
        self.conv3_2 = nn.Conv2d(256, 256, kernel_size=3, padding=1)
        self.relu3_2 = nn.ReLU(inplace=True)
        self.conv3_3 = nn.Conv2d(256, 256, kernel_size=3, padding=1)
        self.relu3_3 = nn.ReLU(inplace=True)
        self.pool3 = nn.MaxPool2d(kernel_size=2, stride=2)

        # conv4 1/16
        self.conv4_1 = nn.Conv2d(256, 512, kernel_size=3, padding=1)
        self.relu4_1 = nn.ReLU(inplace=True)
        self.conv4_2 = nn.Conv2d(512, 512, kernel_size=3, padding=1)
        self.relu4_2 = nn.ReLU(inplace=True)
        self.conv4_3 = nn.Conv2d(512, 512, kernel_size=3, padding=1)
        self.relu4_3 = nn.ReLU(inplace=True)
        self.pool4 = nn.MaxPool2d(kernel_size=2, stride=2)

        # conv5 1/32
        self.conv5_1 = nn.Conv2d(512, 512, kernel_size=3, padding=1)
        self.relu5_1 = nn.ReLU(inplace=True)
        self.conv5_2 = nn.Conv2d(512, 512, kernel_size=3, padding=1)
        self.relu5_2 = nn.ReLU(inplace=True)
        self.conv5_3 = nn.Conv2d(512, 512, kernel_size=3, padding=1)
        self.relu5_3 = nn.ReLU(inplace=True)
        self.pool5 = nn.MaxPool2d(kernel_size=2, stride=2)
        
        # load pretrained params from torchvision.models.vgg16(pretrained=True)
        if pretrained:
            pretrained_model = vgg16(pretrained=pretrained)
            pretrained_params = pretrained_model.state_dict()
            keys = list(pretrained_params.keys())
            new_dict = {}
            for index, key in enumerate(self.state_dict().keys()):
                new_dict[key] = pretrained_params[keys[index]]
            self.load_state_dict(new_dict)

    def forward(self, x):
        x = self.relu1_1(self.conv1_1(x))
        x = self.relu1_2(self.conv1_2(x))
        x = self.pool1(x)
        pool1 = x

        x = self.relu2_1(self.conv2_1(x))
        x = self.relu2_2(self.conv2_2(x))
        x = self.pool2(x)
        pool2 = x

        x = self.relu3_1(self.conv3_1(x))
        x = self.relu3_2(self.conv3_2(x))
        x = self.relu3_3(self.conv3_3(x))
        x = self.pool3(x)
        pool3 = x

        x = self.relu4_1(self.conv4_1(x))
        x = self.relu4_2(self.conv4_2(x))
        x = self.relu4_3(self.conv4_3(x))
        x = self.pool4(x)
        pool4 = x

        x = self.relu5_1(self.conv5_1(x))
        x = self.relu5_2(self.conv5_2(x))
        x = self.relu5_3(self.conv5_3(x))
        x = self.pool5(x)
        pool5 = x

        return pool1, pool2, pool3, pool4, pool5

FCN 网络，结构也很简单，包含了反卷积以及与浅层信息的融合：

class FCNs(nn.Module):
    def __init__(self, num_classes, backbone="vgg"):
        super(FCNs, self).__init__()
        self.num_classes = num_classes
        if backbone == "vgg":
            self.features = VGG()

        # deconv1 1/16
        self.deconv1 = nn.ConvTranspose2d(512, 512, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.bn1 = nn.BatchNorm2d(512)
        self.relu1 = nn.ReLU()

        # deconv1 1/8
        self.deconv2 = nn.ConvTranspose2d(512, 256, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.bn2 = nn.BatchNorm2d(256)
        self.relu2 = nn.ReLU()

        # deconv1 1/4
        self.deconv3 = nn.ConvTranspose2d(256, 128, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.bn3 = nn.BatchNorm2d(128)
        self.relu3 = nn.ReLU()

        # deconv1 1/2
        self.deconv4 = nn.ConvTranspose2d(128, 64, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.bn4 = nn.BatchNorm2d(64)
        self.relu4 = nn.ReLU()

        # deconv1 1/1
        self.deconv5 = nn.ConvTranspose2d(64, 32, kernel_size=3, stride=2, padding=1, output_padding=1)
        self.bn5 = nn.BatchNorm2d(32)
        self.relu5 = nn.ReLU()

        self.classifier = nn.Conv2d(32, num_classes, kernel_size=1)

    def forward(self, x):
        features = self.features(x)

        y = self.bn1(self.relu1(self.deconv1(features[4])) + features[3])

        y = self.bn2(self.relu2(self.deconv2(y)) + features[2])

        y = self.bn3(self.relu3(self.deconv3(y)) + features[1])

        y = self.bn4(self.relu4(self.deconv4(y)) + features[0])

        y = self.bn5(self.relu5(self.deconv5(y)))

        y = self.classifier(y)

        return y

训练，每个 epoch 会保存一个模型，默认保存在./models下：

python train.py

我的训练结果，上面一行是预测值，下面一行是目标值：

5 个 epoch 时：

10 个 epoch 时：

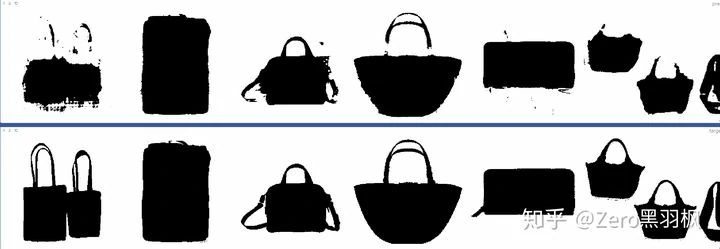
20 个 epoch 时：

---

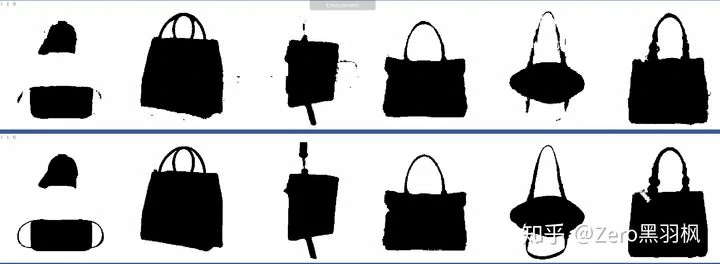
参考资料

https://zhuanlan.zhihu.com/p/77201674
https://medium.com/activating-robotic-minds/up-sampling-with-transposed-convolution-9ae4f2df52d0
https://github.com/FroyoZzz/CV-Papers-Codes