回顾 CNN
通常 CNN 网络在卷积层之后会接上若干个全连接层, 将卷积层产生的特征图(feature map)映射成一个固定长度的特征向量(这就丢失了空间信息)。以 AlexNet 为代表的经典 CNN 结构适合于图像级的分类和回归任务,因为它们最后都期望得到整个输入图像的一个数值描述(概率),比如 AlexNet 的 ImageNet 模型输出一个 1000 维的向量表示输入图像属于每一类的概率(softmax归一化)。
下图中的猫, 输入 AlexNet, 得到一个长为 1000 的输出向量, 表示输入图像属于每一类的概率, 其中在 “tabby cat” 这一类统计概率最高。

传统的基于 CNN 的分割方法:为了对一个像素分类,使用该像素周围的一个图像块作为 CNN 的输入用于训练和预测。这种方法有几个缺点:一是存储开销很大。例如对每个像素使用的图像块的大小为 15 x 15,然后不断滑动窗口,每次滑动的窗口给 CNN 进行判别分类,因此则所需的存储空间根据滑动窗口的次数和大小急剧上升。二是计算效率低下。相邻的像素块基本上是重复的,针对每个像素块逐个计算卷积,这种计算也有很大程度上的重复。三是像素块大小的限制了感知区域的大小。通常像素块的大小比整幅图像的大小小很多,只能提取一些局部的特征,从而导致分类的性能受到限制。
CNN 的输入是图像,输出是一个结果,或者说是一个值,一个概率值。
FCN 提出所追求的是,输入是一张图片是,输出也是一张图片,学习像素到像素的映射。
FCN
全卷积网络(FCN)则是从抽象的特征中恢复出每个像素所属的类别。即从图像级别的分类进一步延伸到像素级别的分类。
FCN 对图像进行像素级的分类,从而解决了语义级别的图像分割(semantic segmentation)问题。与经典的 CNN 在卷积层之后使用全连接层得到固定长度的特征向量进行分类(全联接层+softmax输出)不同,FCN 可以接受任意尺寸的输入图像,采用反卷积层对最后一个卷积层的 feature map 进行上采样, 使它恢复到输入图像相同的尺寸,从而可以对每个像素都产生了一个预测, 同时保留了原始输入图像中的空间信息, 最后在上采样的特征图上进行逐像素分类。
最后逐个像素计算 softmax 分类的损失, 相当于每一个像素对应一个训练样本。下图是 Longjon 用于语义分割所采用的全卷积网络(FCN)的结构示意图:
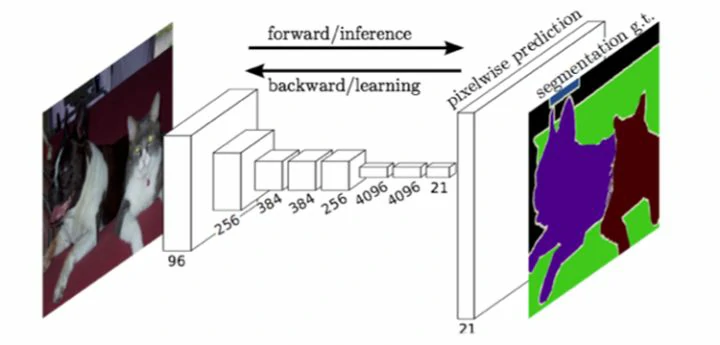
简单的来说,FCN 与 CNN 的区别在把于 CNN 最后的全连接层换成卷积层,输出的是一张已经Label好的图片。因为语义分割需要输出整张图片的分割图,所以要求网络中的特征图至少是二维的,这样才能通过上采样还原到输入图片的同等大小。这就需要替换掉全连接层,改换为卷积层。
全连接层转化为卷积层
- 说一下卷积层和全连接层的区别:卷积层为局部连接;而全连接层则使用图像的全局信息。可以想象一下,最大的局部是不是就等于全局了?这首先说明全连接层使用卷积层来替代的可行性。
- 究竟使用卷积层代替全连接层会带来什么好处呢?答案:可以让卷积网络在一张更大的输入图片上滑动,得到每个区域的输出(这样就突破了输入尺寸的限制)。
论文里 Fully Convolutional Networks for Semantic Segmentation 介绍的很清楚,解读如下:
以 Alexnet 为例,最后一层为 7 x 7 x 256,得到后面 4096 个神经元;但是如果使用 7 x 7 的卷积核对前面的 featuremap 继续卷积(padding=0),不也可以得到 1 x 1 x 4096 的向量吗。如果图片大一点,例如 384 x 384,那么 Alexnet 最后一层大小就是 12 x 12 x 256,经过 7 x 7 卷积核就是 6 x 6 x 4096,这时 6 x 6 = 36 个神经元就有了位置信息,如下图所示:
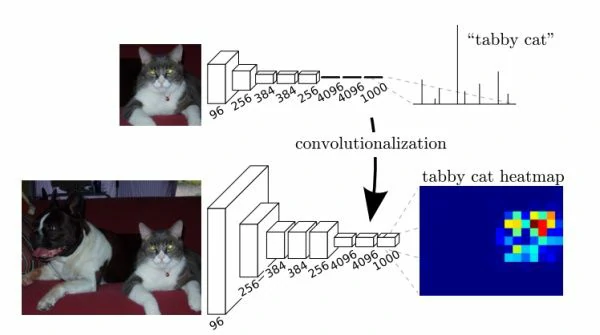
第一个连接区域是 [7 x 7 x 512] 的全连接层,令其滤波器尺寸为 Kernel = 7,这样输出数据体就为 [1 x 1 x 4096] 了;第二个全连接层,令其滤波器尺寸为 Kernel = 1,这样输出数据体为 [1 x 1 x 4096];最后一个全连接层也做类似的,令其 Kernel = 1,最终输出为 [1 x 1 x 1000]。
实际操作中,每次这样的变换都需要把全连接层的权重 W 重塑成卷积层的滤波器。
经过多次卷积(还有 pooling)以后,得到的图像越来越小,分辨率越来越低(粗略的图像),那么 FCN 是如何得到图像中每一个像素的类别的呢?为了从这个分辨率低的粗略图像恢复到原图的分辨率,FCN 使用了上采样。例如经过 5 次卷积(和pooling)以后,图像的分辨率依次缩小了2, 4, 8, 16, 32倍。对于最后一层的输出图像,需要进行 32 倍的上采样,以得到原图一样的大小。
heatmap
heatmap 其实就是 featuremap,本来是很小的图片经过全卷积得到 1 * 1 * n 的特征,那么输入大一点的图片时就会变成 m * m * n,这里的 m * m 就是 heatmap。
上采样
这个上采样是通过反卷积(deconvolution)实现的。对第 5 层的输出(32倍放大)反卷积到原图大小,得到的结果还是不够精确,一些细节无法恢复。于是 Jonathan 将第 4 层的输出和第 3 层的输出也依次反卷积,分别需要 16 倍和 8 倍上采样,结果就精细一些了。下图是这个卷积和反卷积上采样的过程:
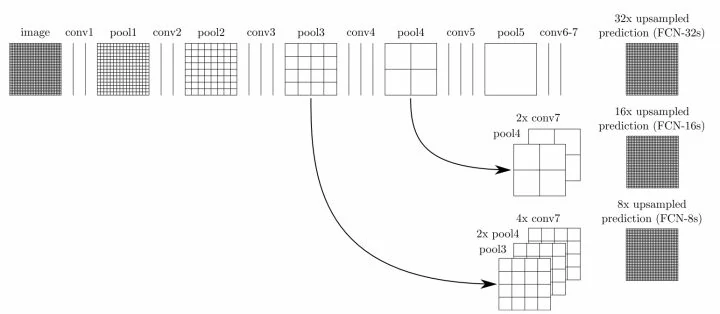
解释一下三次上采样:
如上图所示,对原图像进行卷积 conv1、pool1 后原图像缩小为 1/2;之后对图像进行第二次 conv2、pool2 后图像缩小为 1/4;接着继续对图像进行第三次卷积操作 conv3、pool3 缩小为原图像的 1/8,此时保留 pool3 的 featureMap;接着继续对图像进行第四次卷积操作 conv4、pool4,缩小为原图像的 1/16,保留 pool4 的 featureMap;最后对图像进行第五次卷积操作 conv5、pool5,缩小为原图像的 1/32,然后把原来 CNN 操作中的全连接变成卷积操作 conv6、conv7,图像的 featureMap 数量改变但是图像大小依然为原图的 1/32,此时图像不再叫 featureMap 而是叫 heatMap。
现在我们有 1/32 尺寸的 heatMap,1/16 尺寸的 featureMap 和 1/8 尺寸的 featureMap,1/32 尺寸的 heatMap 进行 upsampling 操作之后,因为这样的操作还原的图片仅仅是 conv5 中的卷积核中的特征,限于精度问题不能够很好地还原图像当中的特征,因此在这里向前迭代。把 conv4 中的卷积核对上一次 upsampling 之后的图进行反卷积补充细节(相当于一个插值过程),最后把 conv3 中的卷积核对刚才 upsampling 之后的图像进行再次反卷积补充细节,最后就完成了整个图像的还原。
下图是 32 倍、16 倍和 8 倍上采样得到的结果的对比,可以看到它们得到的结果越来越精确:
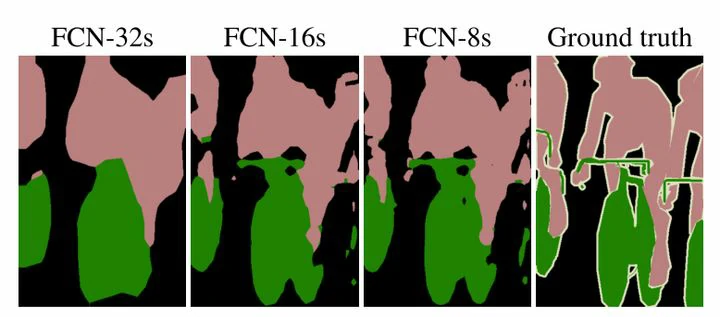
为什么会这样呢?
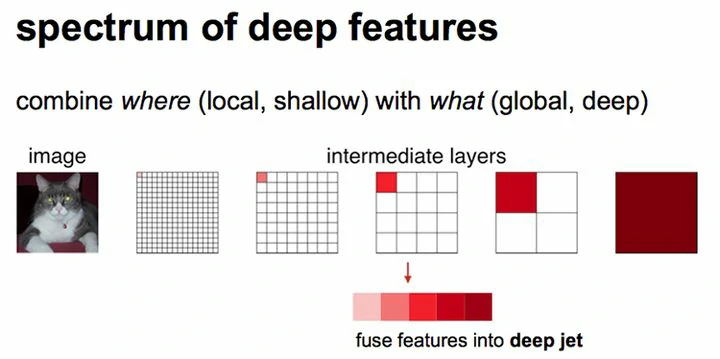
这里就涉及到一个感受域(receptive field)的概念。较浅的卷积层(靠前的)的感受域比较小,学习感知细节部分的能力强,较深的隐藏层(靠后的),感受域相对较大,适合学习较为整体的、相对更宏观一些的特征。所以在较深的卷积层上进行反卷积还原,自然会丢失很多细节特征。
反卷积
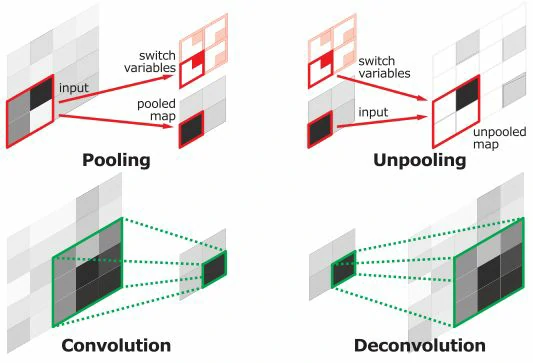
优点和不足:
与传统用 CNN 进行图像分割的方法相比,FCN 有两大明显的优点:一是可以接受任意大小的输入图像,而不用要求所有的训练图像和测试图像具有同样的尺寸。二是更加高效,因为避免了由于使用像素块而带来的重复存储和计算卷积的问题。
同时 FCN 的缺点也比较明显:一是得到的结果还是不够精细。进行 8 倍上采样虽然比 32 倍的效果好了很多,但是上采样的结果还是比较模糊和平滑,对图像中的细节不敏感。二是对各个像素进行分类,没有充分考虑像素与像素之间的关系,忽略了在通常的基于像素分类的分割方法中使用的空间规整(spatial regularization)步骤,缺乏空间一致性。