引言
卷积,是卷积神经网络中最重要的组件之一。不同的卷积结构有着不一样的功能,但本质上都是用于提取特征。比如,在传统图像处理中,人们通过设定不同的算子来提取诸如边缘、水平、垂直等固定的特征。而在卷积神经网络中,仅需要随机初始化一个固定卷积核大小的滤波器,并通过诸如反向传播的技术来实现卷积核参数的自动更新即可。其中,浅层的滤波器对诸如点、线、面等底层特征比较敏感,深层的滤波器则可以用于提取更加抽象的高级语义特征,以完成从低级特征到高级特征的映射。本文将从背景、原理、特性及改进四个维度分别梳理10篇影响力深远的经典卷积模块以及10篇具有代表性的卷积变体,使读者对卷积的发展脉络有一个更加清晰的认知。
【经典卷积系列】
- 原始卷积 (Vanilla Convolution)
- 组卷积 (Group convolution)
- 转置卷积 (Transposed Convolution)
- 1×1卷积 (1×1 Convolution)
- 空洞卷积 (Atrous convolution)
- 深度可分离卷积 (Depthwise Separable Convolution)
- 可变形卷积 (Deformable convolution)
- 空间可分离卷积 (Spatially Separable Convolution)
- 图卷积 (Graph Convolution)
- 植入块 (Inception Block)
【卷积变体系列】
- 非对称卷积(Asymmetric Convolution)
- 八度卷积(Octave Convolution)
- 异构卷积(Heterogeneous Convolution)
- 条件参数化卷积(Conditionally Parameterized Convolutions)
- 动态卷积(Dynamic Convolution)
- 幻影卷积(Ghost Convolution)
- 自校正卷积(Self-Calibrated Convolution)
- 逐深度过参数化卷积(Depthwise Over-parameterized Convolution)
- 分离注意力模块(ResNeSt Block)
- 内卷(Involution)
VanillaConv
背景
CNNs中的卷积,也称为滤波器,是由一组具有固定窗口大小且带可学习参数(learnable paramerters)的卷积核所组成,可用于提取特征。
原理
如下图所示,卷积的过程是通过滑动窗口从上到下,从左到右对输入特征图进行遍历,每次遍历的结果为相应位置元素的加权求和:
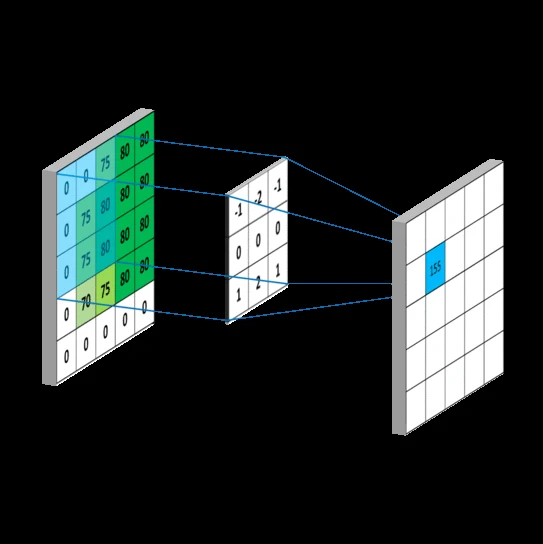
特性
稀疏连接(sparse connectivity)
传统的神经网络层使用矩阵乘法,由一个参数矩阵和一个单独的参数描述每个输入和每个输出之间的交互,即每个输出单元与每个输入单元进行密集交互。
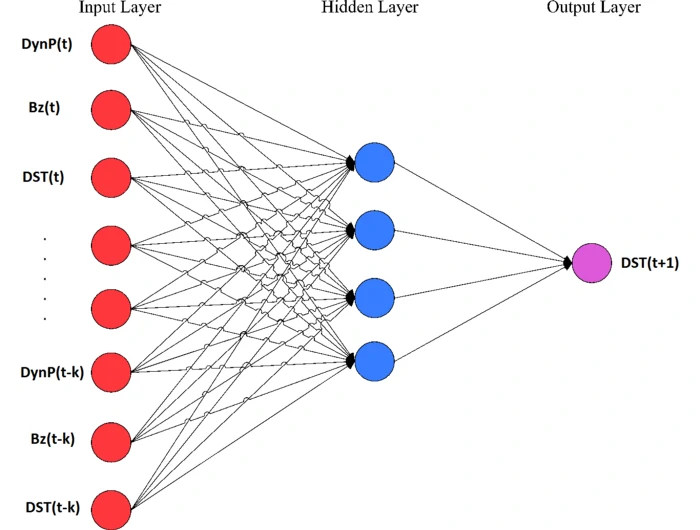
然而,卷积网络具有稀疏交互作用,有时也称为稀疏连接或稀疏权值。
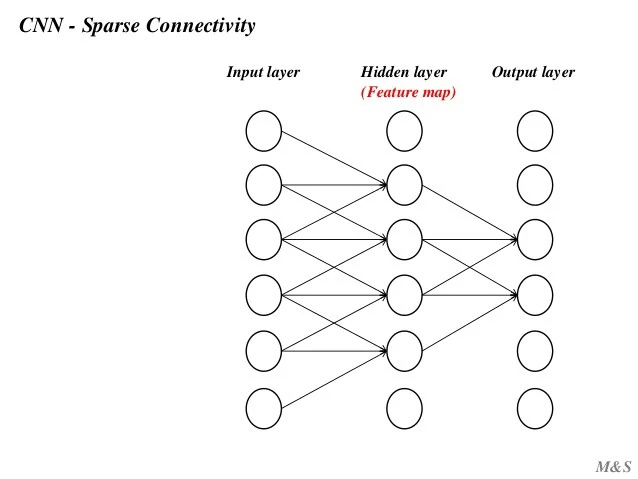
总的来说,使用稀疏连接方式可以使网络储存更少的参数,降低模型的内存要求,同时提高计算效率。
权值共享(shared weights)
在传统的神经网络中,每个元素都使用一个对应的参数(权重)进行学习。但是,在CNNs中卷积核参数是共享的。权值共享,也称为参数共享,是指在计算图层的输出时多次使用相同的参数进行卷积运算。
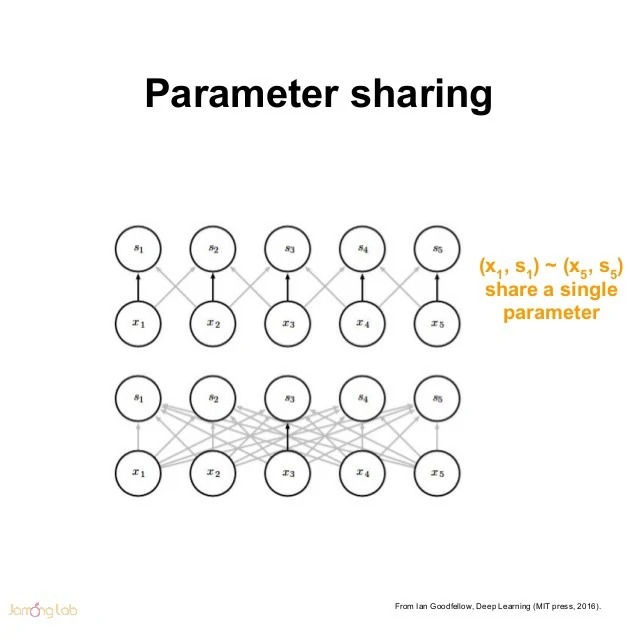
平移不变性(translation invariant)
CNNs中的平移不变性指的是当图像中的目标发生偏移时网络仍然能够输出同源图像一致的结果。对于图像分类任务来说,我们希望CNNs具备平移不变性,因为当图像中目标发生位置偏移时其输出结果应该保持一致。然而,CNNs结构本身所带来的平移不变性是非常脆弱的,大多数时候还是需要从大量数据中学习出来。
平移等变性(translation equivalence)
CNNs中的平移等变性指的是当输入发生偏移时网络的输出结果也应该发生相应的偏移。这种特性比较适用于目标检测和语义分割等任务。CNNs中卷积操作的参数共享使得它对平移操作具有等变性,而一些池化操作对平移有近似不变性。
GroupConv
论文:AlexNet[1] (Accepted by NIPS 2012)
背景
受单个GPU算力的瓶颈限制,组卷积在早期阶段是被应用于切分网络使其能够在多个GPU上进行并行计算,之后被广泛应用到**ResNeXt[2]**网络中。
原理
原始卷积操作中每一个输出通道都与输入的每一个通道相连接,通道之间是以稠密方式进行连接。而组卷积中输入和输出的通道会被划分为多个组,每个组的输出通道只和对应组内的输入通道相连接,而与其它组的通道无关。这种分组(split)的思想随后被绝大多数的新晋卷积所应用。
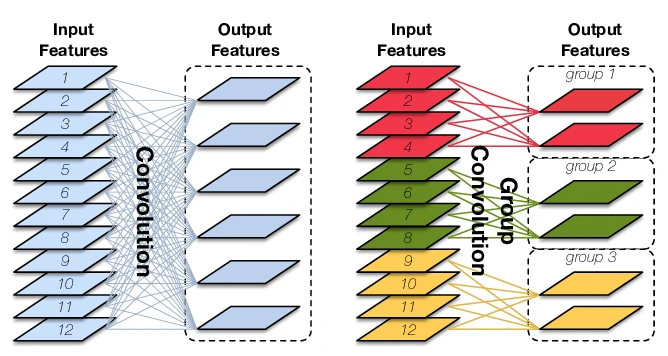
特性
降低参数量
参数量为原始卷积的1/g,其中g为分组数。
提高训练效率
通过将卷积运算按通道划分为多个路径,可以尽可能地利用分布式的计算资源进行并行运算,有利于大规模深度神经网络的训练。
提高泛化性能
组卷积可以看成是对原始卷积操作的一种解耦,改善原始卷积操作中滤波器之间的稀疏性,在一定程度上起到正则化的作用。
改进
原始的组卷积实现中,不同通道的特征会被划分到不同的组里面,直到网络的末端才将其融合起来,中间过程显然缺乏信息的交互(考虑到不同滤波器可提取到不同的特征)。
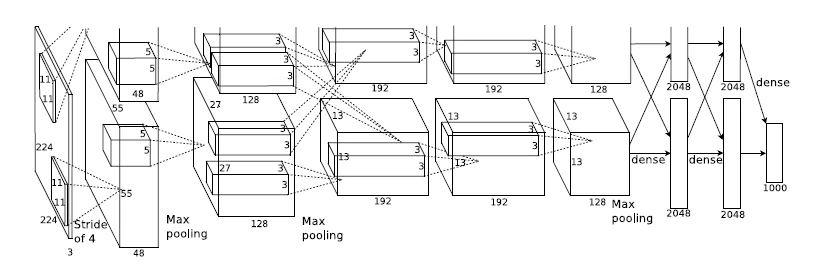
为了解决此问题,**ShuffleNet[3]**结合了逐点组卷积(Pointwise Group Convolution, PGC)和通道混洗(channel shuffle),来实现一个高效轻量化的移动端网络设计。
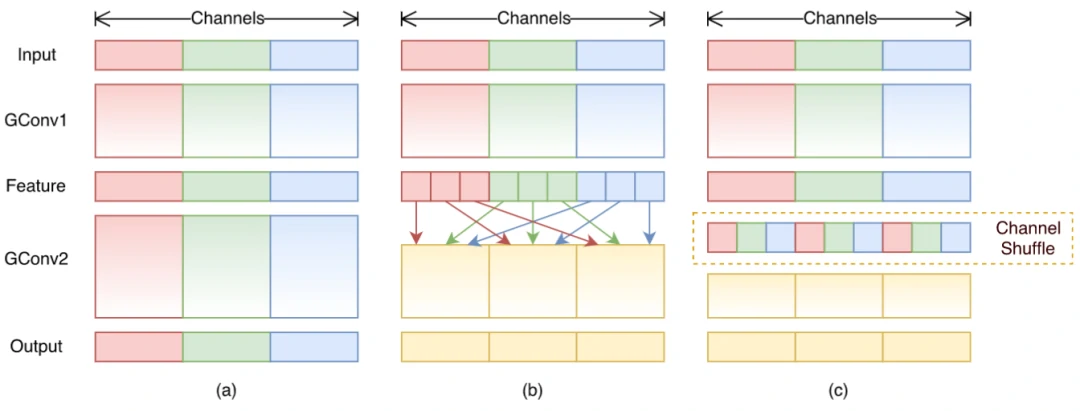
单纯地应用PGC虽然可以有效的降低计算复杂度,但同时也会引入副作用(组与组之间的信息无交互)。因此,作者进一步地应用通道混洗操作来促使信息更好的流通。最后,论文中也提出了一种Shuffle单元。
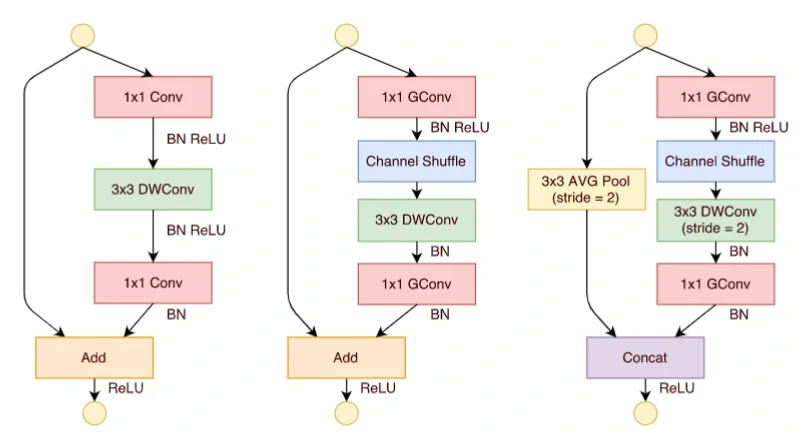
TransposedConv
论文:《A guide to convolution arithmetic for deeplearning》[4]
背景
转置卷积,也称为反卷积(Deconvolution)或微步卷积(Fractionally-strided Convolution),一般应用在编解码结构中的解码器部分或者DCGAN中的生成器中等。但由于数字信号处理中也有反卷积的概念,所以一般为了不造成歧义,大多数框架的API都会定义为转置卷积。
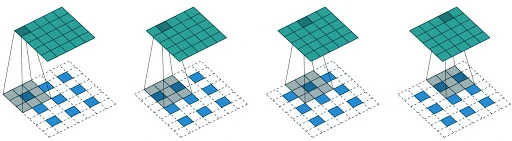
原理
与常规的卷积操作不同,转置卷积是一种一对多的映射关系,即输入矩阵中的一个值映射到输出矩阵的K×K(i.e., kernel size)个值。在具体的实现当中,需要维护一个转置矩阵,这个矩阵参数是可学习的。
特性
特征上采样
利用转置卷积,可以引入参数让网络自动学习卷积核的权重以更好地恢复空间分辨率。一般来说,利用转置卷积来替代常规的上采样操作(最近邻插值、双线性插值即双立方插值)会取得更好的效果(在没有过拟合的情况下),弊端是增大了参数量,且容易出现**网格效应[5]**。
特征可视化
利用转置卷积还可以对特征图进行可视化。有时间的强烈推荐大家去阅读原论文**《Visualizing and Understanding Convolutional Networks》[6]**,有助于帮助大家理解不同深度的各个特征图究竟学到了什么特征。比如,增加网络的深度有利于提取更加抽象的高级语义特征,而增加网络的宽度有利于增强特征多样性的表达。或者是小的卷积核有利于特征的学习,而小的步长则有利于保留更多的空间细节信息。
1×1Conv
论文:《Network In Network》[7] (Accepted by ICLR 2014)
背景
1×1卷积最初提出的目的是用于增强模型对特定感受野下的局部区域的判定能力。后续也被**GoogleNet[8]和ResNet[9]**进一步的应用。
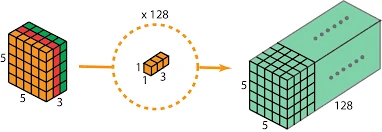
特性
增强特征表达能力
1×1卷积本质上也是一个带参数的滤波器,在不改变特征图本身尺寸的情况下,能够增加网络深度。通过在卷积后通过非线性激活函数可以有效的增强网络的表达能力。
升维和降维
1×1卷积可以通过增加或减少滤波器的数量来实现升维或降维的目的。与全连接层不同,由于卷积是基于权值共享,因此能够有效的降低网络的参数量和计算量。另一方面,降低维度可以认为是通过减少冗余的特征图来降低模型中间层权重的稀疏性,从而得到一个更加紧凑的网络结构。
跨通道的信息交互
类似于多层感知机,1×1卷积本质上就是多个特征图之间的线性组合。因此,通过1×1卷积操作可以轻松实现跨通道的信息交互和整合。
AtrousConv
论文:《Multi-Scale Context Aggregation by Dilated Convolutions》[10] (Accepted by ICLR 2016)
讲解:https://mp.weixin.qq.com/s/DWGqjMruicwIDKhsmossmg
背景
空洞卷积,也称为扩张卷积(Dilated Convolution),最早是针对语义分割任务所提出来的。由于语义分割是一种像素级的分类,经过编码器所提取出的高级特征图最终需要上采样到原始输入特征图的空间分辨率。因此,为了限制网络整体的计算效率,通常会采用池化和插值等上/下采样操作,但这对语义分割这种稠密预测任务来说是非常致命的,主要体现在以下三方面:
- 不可学习:由于上采样操作(如双线性插值法)是固定的即不可学习的,所以并不能重建回原始的空间信息。
- 损失空间信息:引入池化操作不可避免的会导致内部数据结构丢失,导致空间细节信息严重丢失。
- 丢失小目标:经过N次池化(每次下采样2倍),原则上小于2^N个像素点的目标信息将不可重建,这对于语义分割这种密集型预测任务来说是致命的。
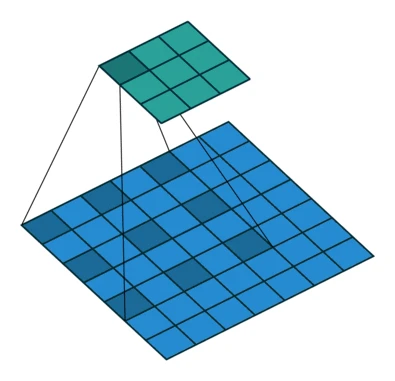
原理
空洞卷积可看成是原始卷积更进一步的扩展,通过在原始卷积的基础上引入空洞率这个超参数,用于调节卷积核的间隔数量。比如,原始卷积核其空洞率为1,而对于空洞率为k的卷积则用0去填充空白的区域。
特性
增大感受野
空洞卷积可以在同等卷积核参数下获得更大的感受野。所以,对于需要较为全局的语义信息或类似于语音文本需要较长的序列信息依赖的任务中,都可以尝试应用空洞卷积。
表征多尺度信息
利用带有不同空洞率的卷积,还可以捕捉到多尺度的上下文语义信息。不同的空洞率代表着不同的感受野,意味着网络能够感知到不同尺寸的目标。
局限性
不好优化
虽然引入空洞卷积可以在参数不变的情况增大感受野,但是由于空间分辨率的增大,所以在实际中常常会不好优化,速度方面是一个诟病,因此在工业上对实时性有要求的应用更多的还是类FCN结构。
引入网格/棋盘效应
应用空洞卷积也引入网格效应。由图森和谷歌大脑合作研究的《Understanding Convolution for Semantic Segmentation》[11]文章指出了如果多次使用空洞率相同的卷积去提取特征时会损失掉信息的连续性。这是因为卷积核并不连续,导致许多的像素从头到尾都没有参与到运算当中,相当于失效了,这对于语义分割这类的密集型预测任务来说是十分不友好的,特别是针对小目标来说。一个解决方案便是令所叠加的卷积其空洞率不能出现大于1的公约数,如令其等于[1, 2, 5],使其呈现锯齿结构。
DWConv
- 论文:《Xception: Deep Learning with Depthwise Separable Convolutions》[12] (Accepted by CVPR 2017)
- 代码:https://github.com/CVHuber/Convolution/blob/main/Depthwise%20Separable%20Convolution.py
- 讲解:https://mp.weixin.qq.com/s/qkldaRnuN-R0B64ssUs47w
背景
深度可分离卷积,由深度卷积(Depthwise Convolution)和逐点卷积(Pointwise Convolution)两部分组成,后也被**MobileNet[13]**等著名网络大规模应用。标准的卷积过程中对应图像区域中的所有通道均被同时考虑,而深度可分离卷积打破了这层瓶颈,将通道和空间区域分开考虑,对不同的输入通道采取不同的卷积核进行卷积,它将普通的卷积操作分解为两个过程,目的是希望能用较少的参数学习更丰富的特征表示。
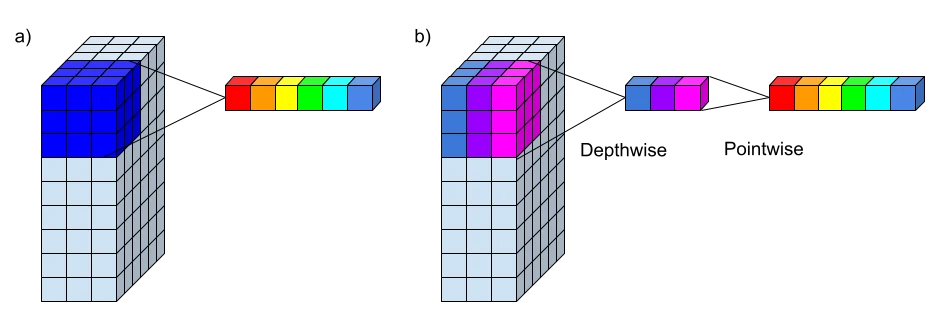
原理
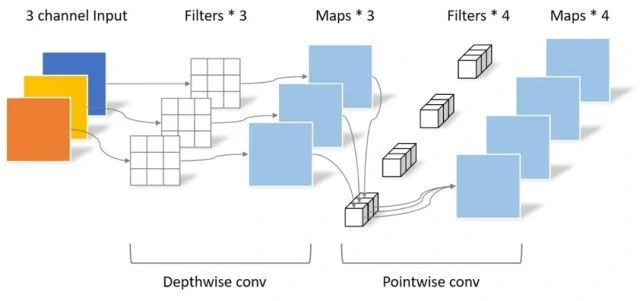
逐深度卷积
不同于原始卷积,深度卷积是一个卷积核负责一个通道,独立地在每个通道上进行空间卷积。因此,深度卷积的输出特征图数量等于输入特征图数量,无法进行有效的维度扩展。
逐点卷积
由于一个特征图仅被一个滤波器卷积,无法有效的利用不同通道在相同空间位置上的特征信息,由此加入了逐点卷积。点卷积主要是要1×1卷积构成,负责将深度卷积的输出按通道投影到一个新的特征图上。
特性
降低参数量和计算量
深度可分离卷积将原始的卷积运算分为两层,一层用于滤波(深度卷积),一层用于组合(逐点卷积)。这种分解过程能极大减少模型的参数量和计算量。
降低模型容量
深度可分离卷积在应用时并没有使用激活函数。此外,虽然深度可分离卷积可以显著的降低模型的计算量,但同时也会导致模型的容量显著降低,从而导致模型精度的下降。
DeformableConv
论文:《Deformable Convolutional Networks》[14] (Accepted by ICCV 2017)
代码:https://github.com/CVHuber/Convolution/blob/main/Deformable%20Convolution.py
讲解:https://mp.weixin.qq.com/s/O9ToEnVC-H7qPwxPQN-a7A
背景
在计算机视觉领域,同一物体在不同场景,角度中未知的几何变换是任务的一大挑战,通常来说要么通过充足的数据增强,扩充足够多的样本去增强模型适应尺度变换的能力,要么设置一些针对几何变换不变的特征或者算法,比如SIFT或者滑动窗口等。然而传统CNNs固定的几何结构无法对未知的物体形变进行有效建模,因此可变形卷积的提出便是用于解决此问题。
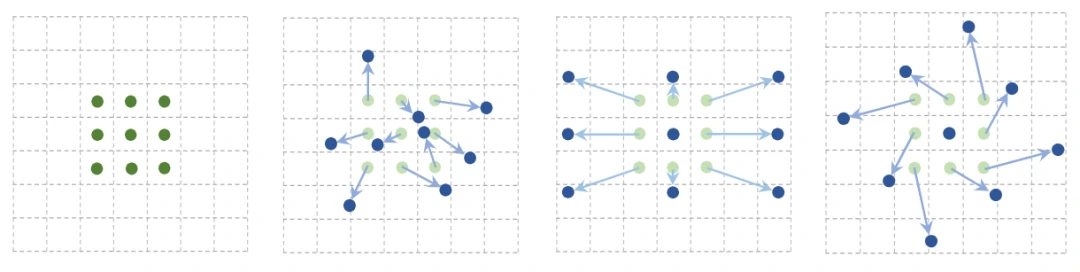
原理
需要注意的是,可变形卷积并不是真正意义上的学习可变形的卷积核,而是利用额外的卷积层去学习相应的偏移量,将得到的偏移量叠加到输入特征图中相应位置的像素点中。但由于偏移量的生成会产生浮点数类型,而偏移量又必须转换为整形,如果直接取整的话是无法进行反向传播的,因此原文是利用双线性插值的方式来间接的计算对应的像素值。
特性
自适应感受野
传统的卷积核由于尺寸形状固定,其激活单元的感受野也相对固定。但实际上同一个物体由于在不同位置上可能对应着不同的尺度或者变形,因此自适应感受野是进行精确定位所需要的,特别是对于密集型预测任务来说。可变形卷积基于一个平行的网络来学习偏移,让卷积核在输入特征图能够发散采样,使网络能够聚焦目标中心,从而提高对物体形变的建模能力。
难以部署
DCN虽然可以带来高精度,但是仍然存在一个缺陷,即当卷积核过大时,会占用非常大的内存空间,因此在落地部署方面的应用很受限制。不过对于参加竞赛而言倒不失为一种提分的trick。
改进
可变形卷积可以在一定程度上提升模型特征提取的泛化能力,但同时也会引入一些不相关的背景噪声干扰。为此,作者提出了改进的版本**《Deformable ConvNets v2: More Deformable, Better Results》[15]**,并给出了三种相应的解决方案:使用更多数量的可变形卷积、为每个偏置都添加相应的权重、模仿R-CNN中的特征。然而,可变形卷积的计算效率也是一个值得商榷的问题。从另一个侧面来看,可变形卷积可以看做是对局部区域进行自注意力操作。
SSConv
背景
与深度可分离卷积一样,空间可分离卷积也属于因式分离卷积的一种,其核心思想是从图像空间维度(宽度和高度)进行卷积运算。
原理
空间可分离卷积的工作原理是将卷积核拆分为两部分,即将一个k×k的卷积核拆成k×1和1×k两个方向的卷积核分别对输入特征图进行卷积,以降低计算的复杂度。
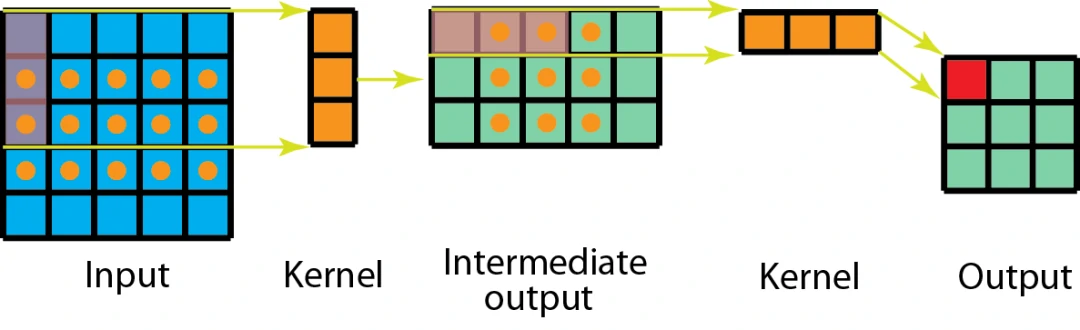
特性
降低计算量
如上图所示,以5×5的输入特征图为例,如果我们直接用一个3×3的卷积核去卷积,共需要9×9=81次乘法运算。而如果换成空间可分离卷积,那么计算量为15×3+9×3=72次乘法运算。共节省了约11%的计算量。
应用
可以在空间上分离的最著名的卷积之一是Sobel算子,用于检测边缘。
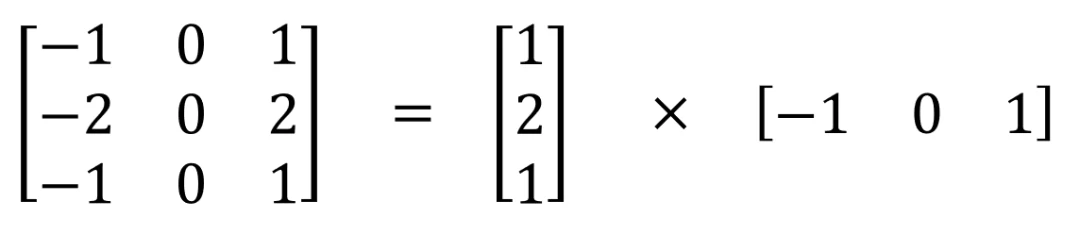
局限性
空间可分离卷积在实际当中很少被广泛应用,最主要的一个原因是并不是所有的卷积核都能够有效的拆分成小的卷积核。
GraphConv
论文:《Semi-Supervised Classification with Graph Convolutional Networks》[16] (Accepted by ICLR 2017)
讲解:https://github.com/CVHuber/Convolution/blob/main/Graph%20Convolution.py
背景
图卷积网络又是图网络中最简单的一个分支,而图卷积的提出便是为了有效的解决传统CNNs、RNNs等网络无法处理的非欧式空间的数据问题。
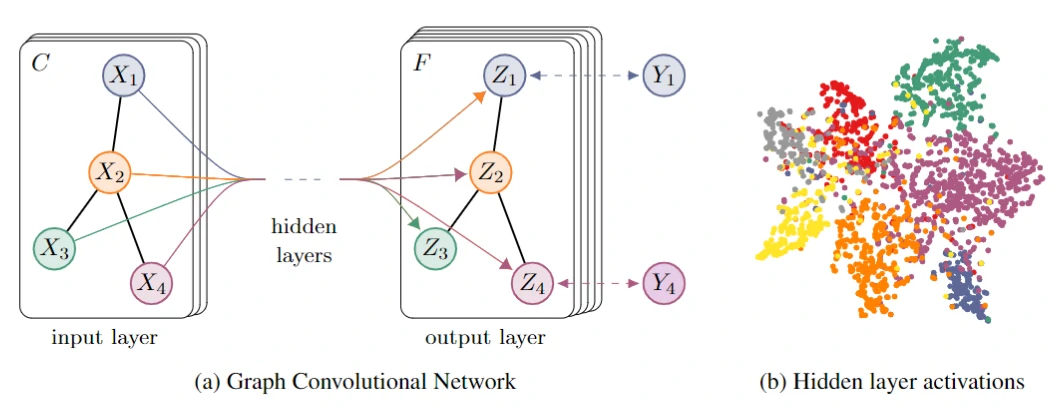
原理
图中的核心思想是利用边的信息对节点信息进行聚合,从而生成新的节点表示。简而言之,CNNs中的卷积运算是卷积核对应位置的加权求和,扩展到GCNs就是利用边的信息不断的汇聚邻间节点的信息,以更新原节点的参数。
特性
节点特征
每个节点均可用于特征表示。
结构特征
节点与节点之间通过携带信息的边进行关联。
Inception Block
论文:Going deeper with convolutions[17] (Accepted by CVPR 2015)
背景
Inception Block最初提出的目的是希望能够在同一层特征图上获得不同尺度下的特征表征,增加网络宽度有利于获得更丰富的特征表示。
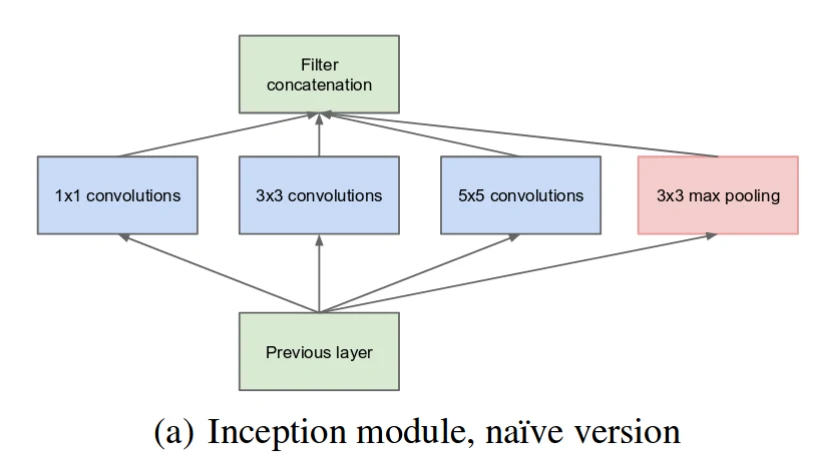
特性
多尺度特征提取
由上图可知,Inception Block主要通过多个带有不同卷积核大小的卷积运算来捕获多尺度的上下文信息,最后再通过拼接操作聚合输出,以获得多尺度特征表示。
改进
Inception v1
为了进一步地压缩网络的参数量和计算量,作者在原先的Inception块中大量的引入了1×1卷积,从而减小网络的整体规模。
Inception v2
**Inception v2[18]的主要思想便是提出了Batch Normalization,通过减少内部协变量偏移有效的加速了深度网络的训练。此外,借鉴VGG-Net[19]**的思想,v2将v1中的5×5卷积用两个3×3卷积进行替换,在保证获得同等感受野的情况下,进一步的降低网络的参数量和计算量。
Inception v3
**Inception v3[20]**主要借鉴了空间可分离卷积的思想,将原本k×k的卷积核拆分成1×k和k×1的一维卷积,一方面可以有效的加速网络的运算,另一方面多余的计算资源可用于增加网络的深度,提高非线性映射的能力。
Inception v4
**Inception v4[21]则借鉴了ResNet[22]**的思想,引入了Skip Connection,不仅可以极大地加速网络的训练,同时也能够显著的提高网络性能。
AsymmetricConv
论文:《ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks》[23] (Accepted by ICCV 2019)
代码:https://github.com/CVHuber/Convolution/blob/main/Asymmetric%20Convolution.py
背景
为特定的应用设计合适的CNNs架构本身涉及到繁重的手动工作或者需要高昂的GPU训练时间,工业界也正在寻求一些CNNs结构可以方便的集成到其他成熟架构中,进一步提升应用到实际任务中的性能。因此,非对称卷积(Asymmetric Convolution)模块提出的目的就是为了能够充分利用已有的成熟组件来构建一个更加高效的网络,在没有增加任何额外的开销的情况下进一步提升网络精度。
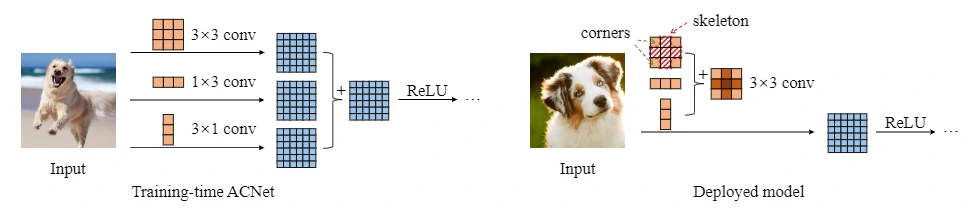
原理
非对称卷积,其核心思想是通过将原始卷积分解,该算法将三个分别具有正方形,水平和垂直核的卷积分支的输出求和。从而在保持精度相当的情况下降低参数量和计算量,形式上利用到前面提到的空间可分离卷积。
特性
无缝衔接
非对称卷积仅引入少量超参数便可方便的与其它结构结合而无需微调,显示增强标注卷积核的特征表达能力。
无损提精
应用非对称卷积可以在没有增加额外的推理时间和计算开销的前提下,有效的提高网络精度,同时增强模型对旋转失真物体的鲁棒性。
改进
原作者在2021年的CVPR会议上进一步提出了ACN v2[24],设计出一种称为Diverse Branch Block的模块,创造性的将Inception的多分支、多尺度思想与过参数化思想进行了一次组合,是一种可以提升CNNs性能且推理耗时无损的通用模块组件。
OctaveConv
论文:坡国立大学以及奇虎360的研究人员联合发表在ICCV 2019的一篇文章《Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution》[25] (Accepted ICCV 2019)
代码:https://github.com/CVHuber/Convolution/blob/main/Octave%20Convolution.py
讲解:https://mp.weixin.qq.com/s/HiHQQaJcrfi5vk_ixPwbIw
背景
在自然图像中,信息以不同的频率传递,其中较高的频率通常用精细的细节编码,较低的频率通常用全局结构编码。同样,卷积层的输出特征图也可以看作是不同频率下信息的混合。在这项工作中,作者提出将混合特征图按其频率分解,并设计一种新的八度卷积操作来存储和处理空间分辨率较低且空间变化较慢的特征图,从而降低了内存和计算成本。与现有的多尺度方法不同,OctConv被表示为一个单一的、通用的、即插即用的卷积单元,可以直接替换普通卷积,而无需对网络架构进行任何调整。Octave本意指的是八音阶,在音乐上代表将声音频率减半的意思,故起名为Octave卷积,旨在对数据中的低频信息减半从而达到加速卷积运算的目的。
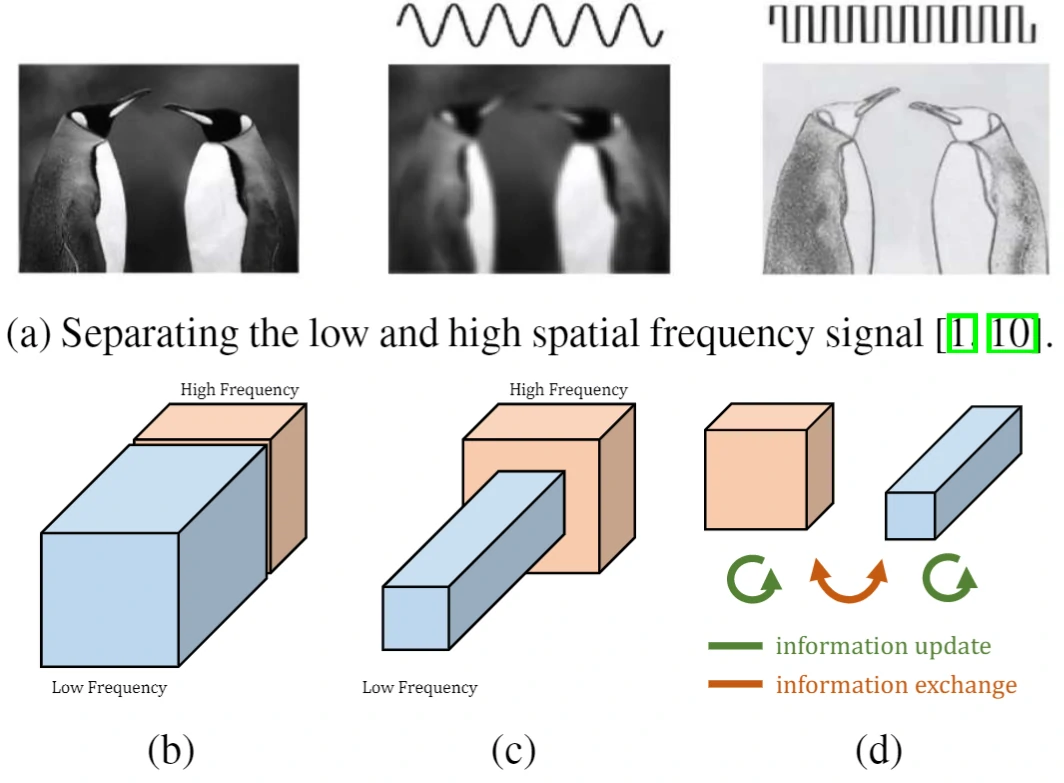
原理
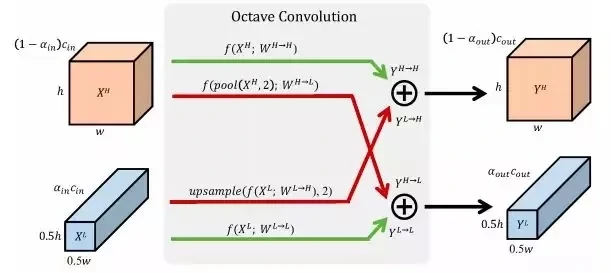
对于普通卷积,所有的输入和输出特征图具有相同的空间分辨率。然而,相关研究表明自然图像可以分解为捕捉全局布局和粗结构的低频信号和捕捉精细细节的高频信号。类似的,卷积输出的特征也应该对应有一个映射子集,它捕获空间低频变化并包含空间冗余信息。为了减少这种空间冗余,引入了Octave特征表示,它显式地将特征映射张量分解为对应于低频和高频的组。**尺度空间理论[26]**为我们提供了一种创建空间分辨率尺度空间的原则方法,用这种方式可以定义低频和高频空间,即将低频特征图的空间分辨率降低一个Octave。
特性
提高效率
由于低频特征图中包含着过多无率用的背景信息,因此可以将低频特征图的空间分辨率降低为原始的一半,减少冗余的空间信息,这也意味着网络的计算开销也随之减少,从而达到加速网络计算效率的目的。
提高精度
与普通卷积相比,压缩低频分辨率有效地将感受野扩大了2倍,进一步帮助每个OctConv层捕获更多的长距离上下文信息,从而提高识别精度。此外,除了频间信息的更新,作者还分别对高/低频特征分别进行升/降采样,以实现不同频率间信息的交互,从而在一定程度上能够提高模型的精度。总的来说,OctConv使用更紧凑的特征表示来存储和处理整个网络中的信息,从而可以达到更好的效率和性能。
HetConv
论文:《HetConv: Heterogeneous Kernel-Based Convolutions for Deep CNNs》[27] (Accepted by CVPR 2019)
代码:https://github.com/CVHuber/Convolution/blob/main/Heterogeneous%20Convolution.py
讲解:https://mp.weixin.qq.com/s/SLN0XmSqtGKmIXVKUUy9rg
背景
提高CNNs精度最直接的做法通常是设计更宽或更深的网络,然而这会带来更高的计算成本。为了降低计算成本,目前已有三类滤波器被广泛地应用,即逐深度卷积(DWC)、逐点卷积(PWC)以及组卷积(GC)。但是,设计一种新架构需要大量研究工作才能找到最优的过滤器组合,进而使得计算成本最小。另一种提升模型效率的常用方法是压缩模型,即通过连接剪枝、过滤器剪枝和量化技术来进一步的减少计算成本。不同于以上方法,异构卷积主要侧重于通过设计新的卷积核来降低给定模型的计算成本,在保证低时延的同时做到精度无损。
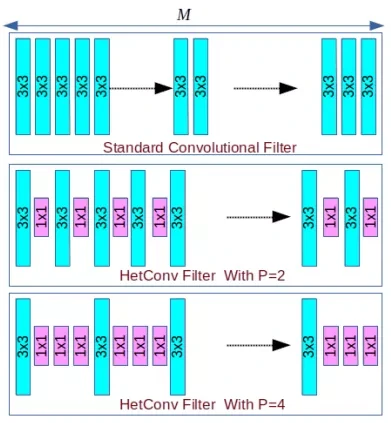
原理
如上图所示,异构卷积的结构设计很简单,即输入特征图的一部分通道应用k×k的卷积核,其余的通道应用1×1的卷积核。其中,P为控制卷积核为k的比例。
特性
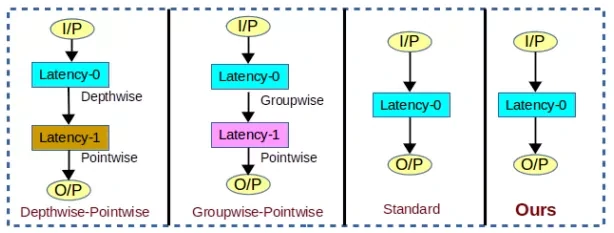
上图展示了不同卷积方式的延迟对比,不难发现第一种和第二种都属于两段式卷积,有一个延迟单元,并且也是目前主流轻量化卷积所使用的。所提出的方法与常规卷积一样是0延迟的。因此,从组成结构上分析可知,所提出的方法的计算成本是比目前主流的轻量化卷积更低的。
CondConv
论文:《CondConv: Conditionally Parameterized Convolutions for Efficient Inference》[28] (Accepted by NIPS 2019)
代码:https://github.com/CVHuber/Convolution/blob/main/Conditionally%20Parameterized%20Convolutions.py
讲解:https://mp.weixin.qq.com/s/bWUrhXfcqiqG4zC_xv_XqA
背景
普通卷积对所有样本都采用相同的卷积核参数,这就导致为了提升模型容量,就需要增加模型的参数。因此提高网络深度,增加通道数是一种常用的做法,但这会进一步导致模型的计算量加大,为部署带来更大的挑战。由此提出了CondConv,它针对每个batch中的每一个输入样本得到定制化的卷积核,在提高模型容量同时还能够保持高效的推理速度。
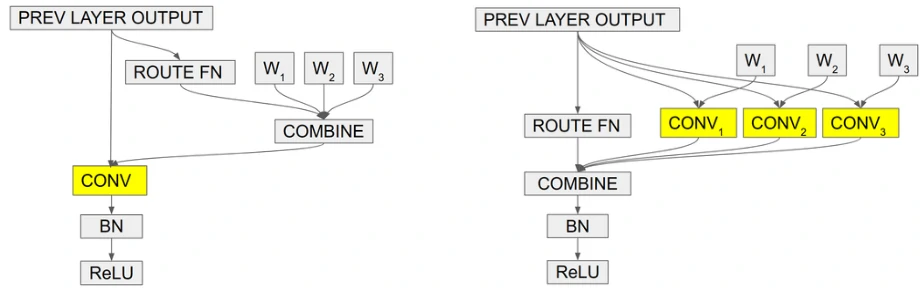
原理
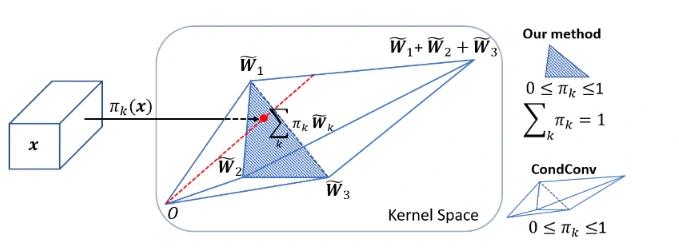
在常规卷积中,卷积核参数一旦经过训练确定以后,无论输入什么样本进行测试,都会利用固定的参数取提取特征。而CondConv中,卷积核参数可以针对输入样本进行动态变换。其次,常规卷积的容量提升依赖于卷积核尺寸和通道数的增加。而CondConv中只需要在执行卷积计算之前通过多个expert对输入样本计算加权卷积核即可。CondConv本质上等价于多个静态卷积的线性组合。
特性
CondConv通过增加内核生成函数的大小和复杂性,利用样本之间的关系改善了模型性能,它为提高模型容量同时保持有效推理提供了一种新的思路。由于仅增加了一个权重向量用于表示卷积核线性组合,因此增加的复杂度比添加其他卷积或扩展现有卷积要少得多。CondConv层可以代替网络中的任何卷积层使用来提高网络的性能,实现即插即用。同时,也可以轻松的扩展到网络层中其它的线性函数上,例如全连接层中的线性函数,提供了一个改进的思路。
DynamicConv
论文:《Dynamic Convolution: Attention over Convolution Kernels》[29] (Accepted by CVPR 2020)
代码:https://github.com/CVHuber/Convolution/blob/main/Dynamic%20Convolution.py
讲解:https://mp.weixin.qq.com/s/zyhZvQXBoadA1m762s2B9g
背景
轻量级卷积神经网络能够在较低的计算预算下运行,却也牺牲了模型性能和表达能力。为此提出了动态卷积,与传统的静态卷积(每层单个卷积核)相比,根据注意力动态叠加多个卷积核不仅显著提升了表达能力,额外的计算成本也很小,因而对高效的 CNN 更加友好,同时可以容易地整合入现有 CNN 架构中。
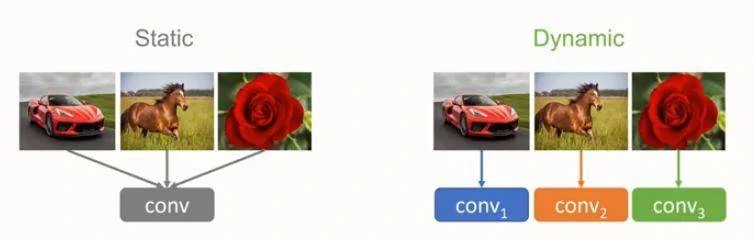
原理
动态卷积的原理根据输入图像,自适应的调整卷积的参数。如上图所示,静态的卷积核对于不同的输入均作同样的处理,而动态的卷积核则会根据输入的不同针对性地利用不同的卷积核选择合适的卷积的参数去进行特征的提取。
特性
权重自适应
动态卷积通过融合注意力机制动态地聚合多个并行的卷积核。首先对输入进行一次注意力操作然后得到每个卷积核的权重,将学习到的权重叠加到不同的卷积核上以实现卷积核的动态选取。
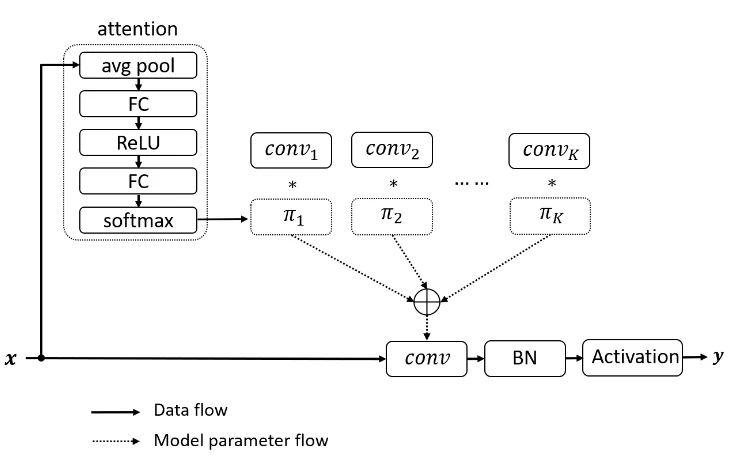
训练方式
动态卷积的一个训练难点在于随着网络深度的加深,如何协调多个卷积核和注意力模型之间的共同学习。作者指出需要限制注意力的取值(令权重和为1)以此来简化注意力模型的学习。其次,在训练初期限制注意力接近均匀分布有利于多个卷积核的共同学习,提出了利用Temperature annealing来提升模型的准确性。
内存计算开销
动态卷积主要包含两部分开销:注意力计算以及卷积核的叠加。其中注意力机制是由GAP和两个FC层组成的,计算复杂度低。而叠加的多个卷积核由于内核尺寸较小,计算复杂度也不高。因此,整体来说动态卷积仅引入了少量额外的计算开销却显著增加了特征表达能力。然而,由于采用多个卷积核并行的方式,必然会极大的增大内存开销。
Ghost Block
论文:《GhostNet: More Features from Cheap Operations》[30] (Accepted by CVPR 2020)
代码:https://github.com/CVHuber/Convolution/blob/main/Ghost%20Convolution.py
讲解:https://mp.weixin.qq.com/s/TBJ7XeBNZYpUpE7kPFEvsA
背景
众所周知,通过堆叠卷积层可以捕获丰富的特征信息,其中也包含了冗余信息,这有利于网络对数据有更全面的理解。因此,可以通过常规卷积操作提取丰富的特征信息,对于冗余的特征信息,则利用更价廉的线性变换操作来生成,这样不仅能够有效地降低模型所需计算资源,同时设计简单、易于实现,可以即插即用。
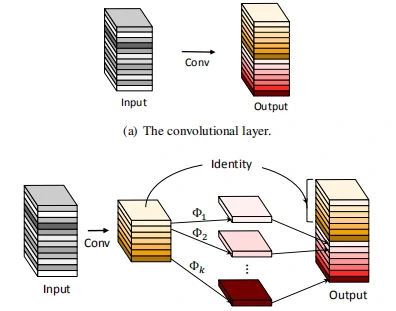
原理
幻影卷积的核心思想是利用简单廉价的线性变化来等效的生成我们所需要的特征图,而无需利用多余的滤波器生成,以此来提高网络的计算效率。
特性
卷积神经网络中主要的参数量和计算量来自于卷积结构,利用卷积可以生成新的特征图,然而并不是所有的特征图都是不一样的。经过可视化分析可以发现存在着很多高度相似的特征图,而这些特征图并没有必要去用卷积获取,而是可以通过简单的线性操作来替代,从而以更小的参数量和计算量换取差不多的精度。Ghost模块使用了分组卷积作为更价廉的线性变换。分组卷积方式消除了通道间的相关性,使得当前通道特征仅与自己相关,一方面模拟冗余特征的生成方式,另一方面显著减低的参数量和计算量。
SCConv
论文:《Improving Convolutional Networks with Self-Calibrated Convolutions》[31] (Accepted by CVPR 2020)
代码:https://github.com/CVHuber/Convolution/blob/main/Self-Calibrated%20Convolution.py
背景
CNNs的最新进展主要致力于设计更复杂的体系结构,以增强其表示学习能力。自校正卷积可以在不调整模型架构的情况下改进CNNs的基本卷积特征转换过程,通过内部通信显着扩展了每个卷积层的感受野,从而丰富了输出功能。特别是,与使用小卷积核融合空间和通道方向信息的标准卷积不同,自校准卷积能够围绕每个空间位置自适应地建立长距离空间和通道间依赖性的校准操作。因此,它可以通过显式合并更丰富的信息来帮助CNNs生成更多辨识性表示。
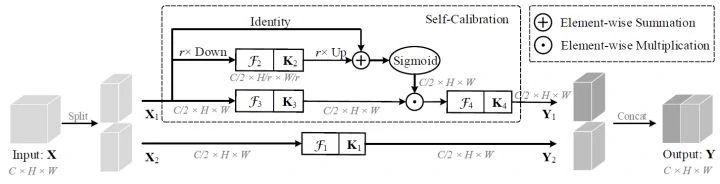
原理
自校正卷积其核心思想是考虑在不调整模型架构的情况下改进CNNs的基本卷积特征转换过程。本质上是一种用于多尺度特征提取的分组卷积,并按通道维度均分为两组。其中一条通路用于常规的卷积提取特征,另一条通路则是利用下采样操作来增大网络的感受野。最终使得每个空间位置都可以通过融合来自两个不同空间尺度的信息来实现自校准的操作。
特性
增强特征表达能力
不同于普通卷积同时融合空间和通道信息,自校正卷积可以通过自校正操作自适应地在每个空间位置周围建立远距离空间和通道的依赖关系,从而生成更具判别力的特征,提取更加丰富的上下文信息。
即插即用
自校正卷积设计简单且通用,可以轻松嵌入到任意的CNN架构中增强卷积层提取特征的能力,而不会引入额外的参数,但不可避免的会增大网络的计算量。
DO-Conv
论文:DO-Conv[32]
代码:https://github.com/yangyanli/DO-Conv
讲解:https://mp.weixin.qq.com/s/fuXYD6EhpoAKxyUJ8xigqg
背景
CNNs应用于计算机视觉领域的很多任务中,增加非线性层的数量,能够有效地增加网络的表达能力,从而提高网络的性能。然而,很少有人考虑只增加线性层,只增加线性层会造成过拟合现象,因为多个连续的线性层可以被一个线性层替代,而使用一个线性层参数更少。因此,作者通过在普通卷积层中加入额外的逐深度卷积,构成一个过参数化的卷积层,并将其命名为DO-Conv。
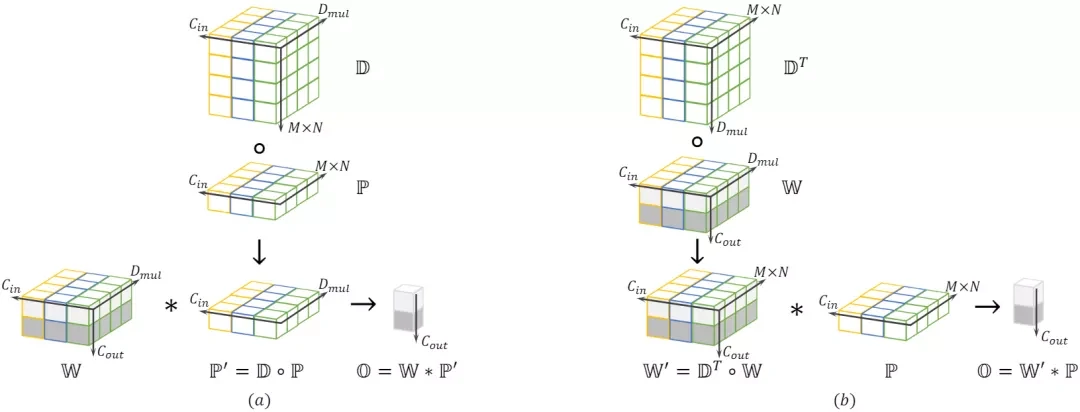
原理
DO-Conv是深度卷积核普通卷积的组合,其计算过程可分为两部分。先对输入特征使用逐深度卷积运算。最后再对输出的中间结果使用常规卷积运算。具体计算过程可参考论文讲解部分。
特性
DO-Conv是一种over-parameterized的卷积层,通过简单的对深度卷积和传统卷积以一定方式组合,代替CNN的普通卷积层,便可以大幅提高CNN的性能。DO-Conv非常方便易用,除了改善了现有CNN的训练速度和最终准确度之外,更无需在模型推理阶段引入额外的计算。
ResNeSt Block
论文:《ResNeSt: Split-Attention Networks》[33]
代码:https://github.com/CVHuber/Convolution/blob/main/ResNeSt%20Block.py
背景
ResNet等一些基础卷积神经网络是针对于图像分类而设计的。由于有限的感受野大小以及缺乏跨通道之间的相互作用,这些网络可能不适合于其它的一些领域像目标检测、图像分割等。这意味着要提高给定计算机视觉任务的性能,需要修改以使其对特定任务更加有效。例如,某些方法添加了金字塔模块或引入了远程连接或使用跨通道特征图注意力。虽然这些方法确实可以提高某些任务的学习性能,但由此而提出了一个问题,即是否可以创建具有通用改进功能表示的通用骨干网,从而同时提高跨多个任务的性能?跨通道信息在下游应用中已被成功使用 ,而最近的图像分类网络更多地关注组或深度卷积。尽管它们在分类任务中具有出色的计算能力和准确性,但是这些模型无法很好地转移到其他任务,因为它们的孤立表示无法捕获跨通道之间的关系。因此,作者提出了ResNeSt block来进行跨通道的学习。
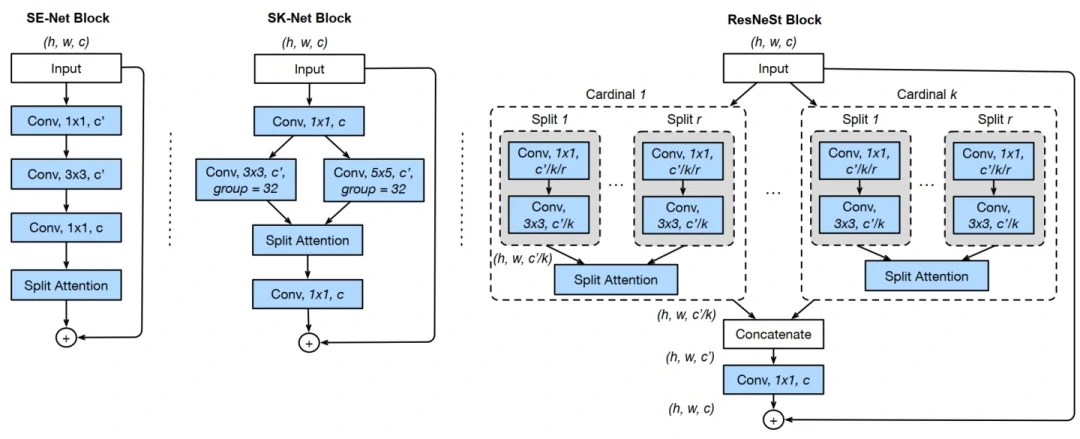
原理
ResNeSt首先是基于ResNeXt,将输入特征图划分为k个组(Cardinal Groups),然后对每个Cardinal Group结SK的思想又划分为r个基(Radix),每个基中又结合了SE的思想。每个Cardinal Groups的操作保持一致,先对组内的各个基特征进行一个1×1+3×3的组合,以压缩通道并进行卷积提取;其次,对所有卷积过后的基特征进行融合,随后利用SE的操作来获取注意力权重;紧接着将学习到的权重叠加回各组基特征,以实现强化和抑制的作用,然后对所有基特征进行融合(Add);最后,结合残差的思想将各个组的输出共同连接起来作为RexNeSt模块的输出。
特性
与现有的ResNet变体相比,ResNeSt不需要增加额外的计算量,同时也可以作为其它任务的骨架。利用ResNeSt主干的模型能够在图像分类、目标检测、实例分割和语义分割这几个任务上达到最先进的性能。与通过神经架构搜索生成的最新CNNs模型相比,所提出的ResNeSt性能优于所有现有ResNet变体,并且具有相同的计算效率,甚至可以实现更好的速度精度折衷。
内卷(Involution)
论文:《Involution: Inverting the Inherence of Convolution for Visual Recognition》[34] (Accepted by CVPR 2021)
代码:https://github.com/CVHuber/Convolution/blob/main/Involution.py
讲解:https://mp.weixin.qq.com/s/Y-hXabMclEcDfvLcxvpKdA
背景
与经典的图像滤波方法类似,卷积核具有两个显著的特性:空间不变性(Spatial-agnostic)和通道特异性(Channel-specific)。前者保证了不同空间区域之间权值共享,实现了平移不变性;后者负责将特征信息编码到不同的通道中,增强了特征表达。虽然这两种特性能够提升对于图像数据的学习效率,但是还存在以下两个主要问题:空间维度上剥夺了卷积核捕获不同空间位置的多种特征表示能力;通道维度上卷积内部的通道间会有冗余。
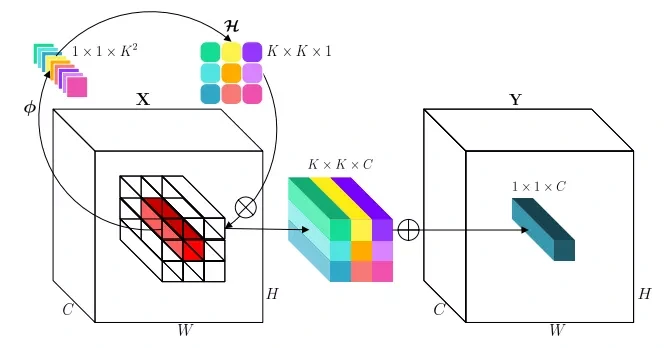
原理
生成内卷核
选取某个空间位置的所有通道像素(红色长方形),通过变换函数并展开获得内卷核(K×K×1)。
计算内卷积
进行乘和操作,即先把内卷核拉成K×K×C,与对应位置相乘,再将K×K个1×1×C相加,代替原来位置的像素,完成内卷积计算。
特性
权重自适应
通过将权重自适应地分配到不同的位置,对不同信息量的特征进行优先级排序。(常规卷积对于不同的位置,都是应用一样权重)
建模上下文
在更广阔的空间中聚合上下文,从而克服对远距离依赖建模的困难。(常规卷积通常使用小卷积核,感受野有限)
共享内卷核
通过共享内卷核,可以减少卷积核的冗余信息。
总结
大多数的卷积结构都是在精度-参数量-计算量这三个维度上进行不同的侧重取舍。两个矛盾:
- 追求计算效率的卷积结构由于计算预算较低,无论是限制卷积层的深度,还是限制了卷积的宽度,不可避免地会导致性能的下降。
- 追求精度提升的卷积结构由于其引入过多的卷积运算或其他额外的操作(如注意力),势必会增大内存或计算开销,从而影响模型的容量和整体的训练或推理速度。
一个设计的原则就是我们如何在不增加额外参数量的情况下,尽可能利用有效的信息或者从降低冗余空间信息的角度出发,来提高模型的计算效率和卷积提取特征的能力。不知道大家看出来了没有,其实大多数的结构都是基于 Split-Transform-Merge 的架构进行改造的。Split指的是分组,可以按需要划分为N组,N=1,2,3…。然后对每一组做一个Transform,即转换,这里可以是利用门控/注意力机制去增强,也可以是利用池化等操作去扩大感受野,亦或是其他操作等等。最后再利用某种机制(如残差)将多组结果合并起来作为输出。可以看出,大多数卷积都是基于STM架构针对每个环节进行设(魔)计(改)。
关于更多的卷积源码现已整理归档,有兴趣的读者可以自行进行到github库下载,后面有更优秀的卷积变体也会持续更新。【代码链接:https://github.com/CVHuber/Convolution,欢迎Star!】
参考资料
https://mp.weixin.qq.com/s?__biz=MzU1MzY0MDI2NA==&mid=2247489799&idx=1&sn=5c42a900537b134af1656bf742d457a1
[1] https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf
[2] https://arxiv.org/abs/1611.05431
[3] https://arxiv.org/abs/1707.01083
[4] https://arxiv.org/abs/1603.07285
[5] https://distill.pub/2016/deconv-checkerboard/
[6] https://arxiv.org/abs/1311.2901
[7] https://arxiv.org/abs/1312.4400
[8] https://arxiv.org/abs/1409.4842
[9] https://arxiv.org/abs/1512.03385
[10] https://arxiv.org/abs/1511.07122
[11] https://arxiv.org/abs/1702.08502
[12] https://arxiv.org/abs/1610.02357
[13] https://arxiv.org/abs/1704.04861
[14] https://arxiv.org/abs/1703.06211
[15] https://arxiv.org/abs/1811.11168
[16] https://arxiv.org/abs/1609.02907
[17] https://arxiv.org/abs/1409.4842
[18] http://arxiv.org/abs/1502.03167
[19] https://arxiv.org/abs/1409.1556
[20] http://arxiv.org/abs/1512.00567
[21] http://arxiv.org/abs/1602.07261
[22] https://arxiv.org/abs/1512.03385
[23] https://arxiv.org/abs/1908.03930
[24] https://link.zhihu.com/?target=https%3A//arxiv.org/pdf/2103.13425.pdf
[25] https://arxiv.org/abs/1904.05049
[26] Scale-space theory in computer vision
[27] https://arxiv.org/abs/1903.04120
[28] https://arxiv.org/pdf/1904.04971
[29] https://arxiv.org/abs/1912.03458
[30] https://arxiv.org/abs/1911.11907
[31] https://openaccess.thecvf.com/content_CVPR_2020/papers/Liu_Improving_Convolutional_Networks_With_Self-Calibrated_Convolutions_CVPR_2020_paper.pdf
[32] https://arxiv.org/pdf/2006.12030
[33] https://arxiv.org/abs/2004.08955
[34] https://arxiv.org/abs/2103.06255